Внешние и внутренние силы. Метод сечений

Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые на­зываются внешними. Внешние силы, действующие на тело, мож­но разделить на активные (независимые) и реактивные. Реак­тивные усилия возникают в связях, наложенных на тело, и опреде­ляются действующими на тело активными усилиями.

По способу приложения внешние силы делятся на объемные и поверхностные.

Объемные силы распределены по всему объему рассматривае­мого тела и приложены к каждой его частице. В частности, к объ­емным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных сил является сила, отнесенная к единице объема - кН/м³.

Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рас­сматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки под­разделяются на сосредоточенные и распределенные. К первым от­носятся нагрузки, реальная площадь приложения которых несоиз­меримо меньше полной площади поверхности тела (например, воз­действие колонн на фундаментную плиту достаточно больших раз­меров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Примером может служить собственный вес балки, действие снеговой или ветровой нагрузки на сооружение, давление жидкости в резервуаре. Распределенная нагрузка может действовать и по линии как, например, при соприкасании двух цилиндров при параллельном расположении их осей. Сосредоточенные усилия измеряются в кН, а распределенные - кН/м² или кН/м.

По времени действия внешние нагрузки (силы) разделяются на постоянные и временные. Собственный вес зданий – это постоянно действующая нагрузка; поезд, идущий через мост, - это нагрузка временная.

По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. Динамические нагрузки - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию.

Взаимодействие между частями рассматриваемого тела характе­ризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмоле­кулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой.

В брусе сечение проводят перпендикулярно его оси. Такое сечение называют поперечным.

Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.

Рассмотрим тело, имеющее форму бруса (рис. 1.4, а).

Пусть к нему приложена некоторая система внешних сил Р ₁, Р ₂, Р ₃,..., Р_n, удовлетворяющая условиям равновесия, т.е. при дейст­вии указанных внешних сил тело находится в состоянии равнове­сия.

Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (P_А ), действующей в сечении А (рис. 1.4, б).

Рис. 1.4

 

Обозначая через 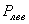и суммы внешних сил, приложен­ных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что

(1.1)

для отсеченных частей бруса получим следующие очевидные соот­ношения:

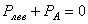; . (1.2)

Последние соотношения показывают, что равнодействующая внутренних сил Р_А в сечении А может определяться с равным успе­хом из условий равновесия либо левой, либо правой частей рассе­ченного тела. В этом суть метода сечений.

Внутренние усилия должны быть так распределены по сече­нию, чтобы деформированные поверхности сечения А при совме­щении правой и левой частей тела в точности совпадали. Это тре­бование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

Воспользуемся правилами статики и приведем систему внут­ренних сил к центру тяжести сечения А в соответствии с прави­лами теоретической механики. В результате получим главный век­тор сил и главный вектор момента (рис. 1.5). Далее выбира­ем декартову систему координат xyz с началом координат, совпада­ющим с центром тяжести сечения А. Ось направим по нормали к сечению, а ос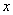и и 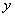расположим в плоскости сечения. Спроекти­ровав главный вектор сил и главный момент на координат­ные оси x, y, z, получаем шесть составляющих: три силы N_z , Q_x , Q_y и три момента M_z , M_x , M_y , называемых внутренними силовы­ми факторами в сечении бруса.

Составляющая N_z называется нормальной, или продольной си­лой в сечении. Силы Q_x и Q_y называются поперечными усилиями. Момент M_z называется крутящим моментом, а моменты M_x и M_y - изгибающими моментами относительно осей x и y, соответственно.

При известных внешних силах все шесть внутренних силовых факторов в сечении определяются из шести уравнений равновесия, которые могут быть составлены для отсеченной части.

Пусть R^*, M^* - результирующая сила и результирующий момент, действующие на отсеченной части тела. Если тело при действии полной системы внешних сил находится в равновесном состоянии, то условия равновесия отсеченной части тела имеет вид:

(1.3)

Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:

(1.4)

которые, в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: , , , , , .

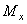Рис. 1.5

 

Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.

В общем случае в сечении могут иметь место все шесть силовых факторов. Однако достаточно часто на практике встречаются случаи, когда некоторые внутренние усилия отсутствуют - такие виды нагружения бруса получили специальные названия (табл.1.1).

 

Таблица 1.1. Простейшие случаи сопротивления

Вид напряженного состояния	Nz	Qx	Qy	Mz	Mx	My
Растяжение/сжатие	+
Кручение				+
Чистый изгиб относительно оси х					+
Чистый изгиб относительно оси у						+
Поперечный изгиб относительно оси х			+		+
Поперечный изгиб относительно оси у		+				+

Примечание: + означает наличие усилия, 0 - его отсутствие.

 

Сопротивления, при которых в поперечном сечении бруса дей­ствует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий (например, изгиб с кручением) сопротивление бруса называется сложным.

В заключение заметим, что при выполнении практических рас­четов, для наглядности, как правило, определяются графики функ­ций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изме­нения внутренних усилий вдоль продольной оси стержня называ­ются эпюрами.

 

Напряжения

При определении внутренних силовых факторов их считают приложенными в центре тяжести сечения. В действительности внутренние силы, являясь результатом взаимодействия частиц тела, непрерывно распределены по сечению. Интенсивность этих сил в разных точках сечения может быть различной. При увеличении нагрузки на элемент конструкции увеличиваются внутренние силы и соответственно увеличивается их интенсивность во всех точках сечения. Если в некоторой точке интенсивность внутренних сил достигнет определенного для данного материала значения, в этой точке возникает трещина, развитие которой приведет к разрушению элемента, или возникнут недопустимые пластические деформации. Следовательно, о прочности элементов конструкций следует судить не по значению внутренних силовых факторов, а по их интенсивности. Меру интенсивности внутренних сил называют напряжением.

В окрестности произвольной точки, принадлежащей сечению некоторого нагруженного тела, выделим элементарную площадку , в пределах которой действует внутреннее усилие 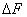(рис. 1.6, а).

Среднее значение интенсивности внутренних усилий на площадке, называемое средним напряжением, определяют по формуле

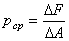(1.5)

Уменьшая площадь , в пределе получаем истинное напряжение в данной точке сечения

(1.6)

Векторная величина называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па).

Разложим вектор полного напряжения на две составляющие (рис.1.6, б).

Проекция вектора полного напряжения на нормаль к данной площадке обознача­ется через и называется нормальным напряжением.

Рис. 1.6

Составляющую, лежащую в сечении в данной площадке обознача­ется через и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и 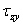(рис.1.6, в). Первый индекс при показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.

Между полным напряжением и его составляющими существует зависимость

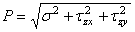(1.7)

Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.

Совокуп­ность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью . По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 1.7)

; ; .

Рис.1.7

 

Соответствующие элементарные моменты относительно координатных осей 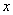, , 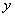имеют вид:

; ; .

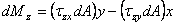Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями:

(1.8)

В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениями , и 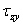, выражение для можно записать в виде

,

где

.

Интегральные зависимости (1.8) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению.

Перемещения и деформации

Под действием внешних сил твердые тела изменяют свою гео­метрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор 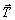, имеющий свое начало в точке А недефор­мированного состояния, а конец в т. деформированного состоя­ния, называется вектором полного перемещения т. А (рис. 1.8, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформиро­ванного состояния, расположенные на расстоянии 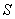друг от друга (рис. 1.8, б).

Рис. 1.8

 

Пусть в результате изменения формы тела эти точки перемес­тились в положение и , соответственно, а расстояние между ними увеличилось на величину D S и составило S + D S. Величина

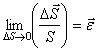(1.9)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей , то в обозначения соответствующих проекций линейной деформации вводятся индексы , , .

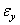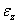Линейные деформации , , 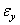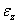характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрез­ками ОD и ОС (рис. 1.8, б). При действии внешних сил указанный угол DOC изменится и примет новое значение 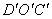. Величина

(1.10)

называется угловой деформацией, или сдвигом в точке О в плос­кости СОD. Относительно координатных осей деформации сдвига обозначаются , , .

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформиро­ванное состояние в точке.