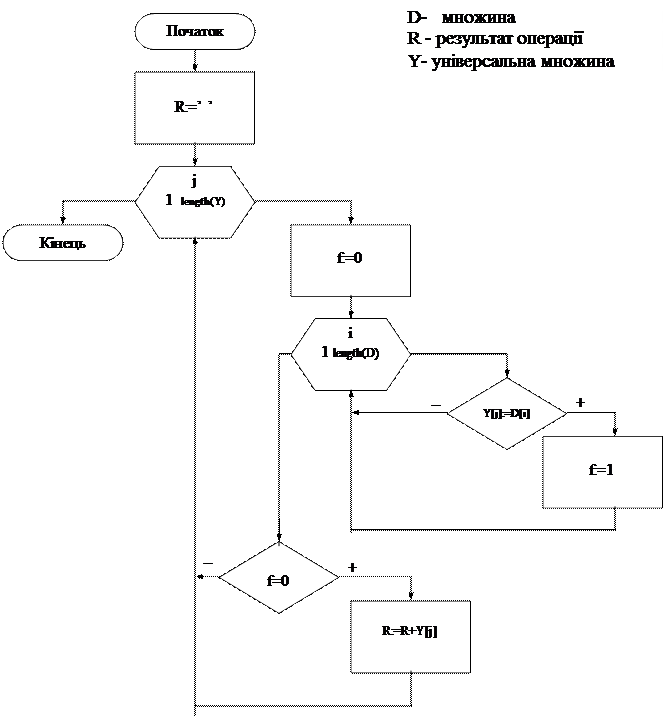
Доповнення множини
procedure DOPOLN(D:string; var R:string)
 | |||
|
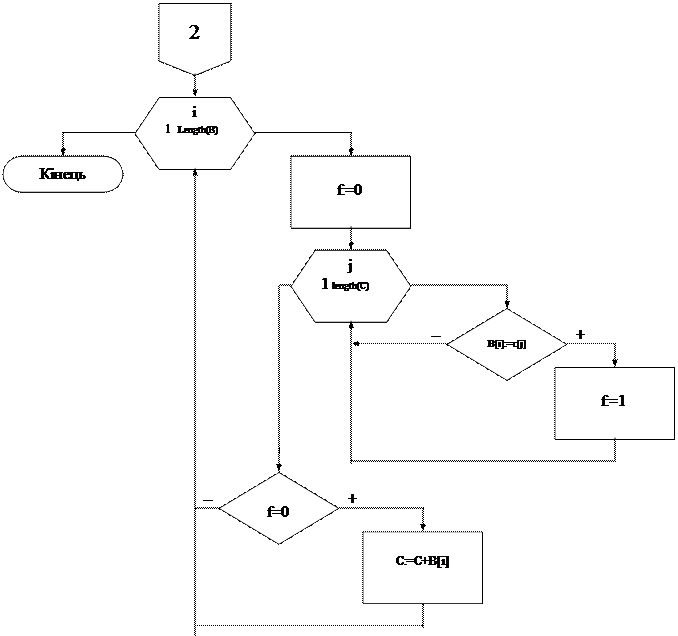
Об'єднання двох множин
Procedure JOIN (A, B: string; var C: string)

|
 | |||
|
Перетинання двох множин
Procedure PERESECH (A, B: string; var C: string)

|
Різниця двох множин Симетрична різниця двох множин множин
Procedure RAZNOST procedure SYMRAZNOST
(A, B: string, var C:string) (A, B: string, var C:string)
 | |||
 | |||
|
|
Лабораторна робота №10
Тема: «Функції теорії множин».
Мета: вивчити основні аксіоми, закони і теореми теорії множин, навчитися застосовувати їх на практиці.
Завдання:
- Виконати обчислення по заданій формулі;
- скласти алгоритм і написати програму, що буде обчислювати функцію множин (згідно свого варіанта, приведеного в табл. 3);
- використовувати матеріали л.р. № 9.
Варіанти завдань приведені в табл. 3 додатку А.
Теоретичні основи:
Основні закони операцій перетинання й об'єднання
1. Закон комутатівності-
А  В=В
В=В  А; А
А; А  В=В
В=В  А
А
2. Закон асоціативності
(А  В)
В)  С=А
С=А  (B
(B  С)
С)
(А  В)
В)  C=А
C=А  (B
(B  С)
С)
3. Закони дистрибутивності:
1-ий – (А  В)
В)  C=(А
C=(А  C)
C)  (B
(B  C)
C)
2-ий - (А  В)
В)  C=(А
C=(А  C)
C)  (B
(B  C)
C)
4. Закони де Моргана.
 | |||
 | |||
А  В= А
В= А  В А
В А  В= А
В= А  В
В
Приклади деяких операцій над множинами.
Довести тотожності.
1. А\(B  C)=(А\B)
C)=(А\B)  (А\C)
(А\C)
(А  В)
В)  (А
(А  C)=А\(B
C)=А\(B  C)- доведено
C)- доведено
2.  А\(А\B)=А
А\(А\B)=А  В
В
А\(А  В)=А
В)=А  (А
(А  В)=А
В)=А  (А
(А  В)=А
В)=А  А
А  А
А  В=А
В=А  В- доведено
В- доведено
3. А  В=А
В=А  (B\А)
(B\А)
А  (В
(В  А)=А
А)=А  В
В  А
А  А=А
А=А  В
В  I=А
I=А  В- доведено
В- доведено
Контрольні питання:
1. Основні закони теорії множин.
2. Функції від множин. Форми представлення.
3. Методи мінімізації функції від множин.
Лабораторна робота №11
Тема: Логічні функції двох змінних.
Мета: вивчити логічні функції двох змінних, навчитися одержувати досконалу диз'юнктивну нормальну форму й досконалу кон’юктивну нормальну форму та приводити функцію до заданого базису.
Завдання:
Для заданого варіанта логічної функції  потрібно скласти алгоритм та програму, що дозволяють виконувати наступні дії:
потрібно скласти алгоритм та програму, що дозволяють виконувати наступні дії:
а) реалізовувати логічні функції двох змінних;
б) побудувати таблицю істинності для заданої функції (довільної);
в) побудувати досконалу диз'юнктивну нормальну форму (ДДНФ) і досконалу кон’юктивну нормальну форму (ДКНФ) для заданої у індивідуальних завданнях функції (а також довільної);
Зробити аналіз роботи програми за допомогою розрахунку таблиці істинності заданої функції.
Варіанти завдань приведені в табл. 4 додатку А.
Теоретичні основи:
Функції двох змінних алгебри логіки
Алгебра A = <B, F>, у якій множина B={0,1}, а F є множина операцій f: Bn®B, n=1, 2,...,m, називається алгеброю логіки або булевою.
Операції f: Bn®B називаються функціями алгебри логіки або логічні функції, булевими (БФ).
Усяка логічна функція f(x1,x2,..., xn) може бути задана таблицею, що називається таблицею істинності.
Логічних функцій двох змінних – 16, вони наведені в табл. 1
Таблиця 1
Функції двох змінних алгебри логіки
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
БФ  й
й  - константи 0 й 1, тобто функції із двома несуттєвими змінними.
- константи 0 й 1, тобто функції із двома несуттєвими змінними.
Функція  називається кон’юнкцією, логічним множенням
називається кон’юнкцією, логічним множенням  й
й 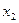 ; її позначення:
; її позначення:  ,
,  або
або 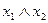 . Вона дорівнює 1, тільки якщо
. Вона дорівнює 1, тільки якщо  й
й 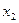 рівні 1.
рівні 1.
Функція  .
.
Функція  .
.
Функція  .
.
Функція  .
.
Функція  – це додавання по модулю 2. Її позначення:
– це додавання по модулю 2. Її позначення:  . Вона дорівнює 1, коли значення її аргументів різні.
. Вона дорівнює 1, коли значення її аргументів різні.
Функція  називається диз'юнкцією, логічною сумою
називається диз'юнкцією, логічною сумою  й
й 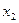 ; її позначення:
; її позначення:  ,
,  . Вона дорівнює 1, якщо х1 або х2 дорівнює 1.
. Вона дорівнює 1, якщо х1 або х2 дорівнює 1.
Функція  називається функцією Вебба або стрілкою Пірса; її позначення:
називається функцією Вебба або стрілкою Пірса; її позначення: 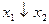 . Вона дорівнює 1 тоді й тільки тоді, коли обидва аргументи рівні 0.
. Вона дорівнює 1 тоді й тільки тоді, коли обидва аргументи рівні 0.
Функція  називається еквівалентністю; її позначення:
називається еквівалентністю; її позначення:  ,
,  . Вона дорівнює 1, коли значення її аргументів рівні.
. Вона дорівнює 1, коли значення її аргументів рівні.
Функція  .
.
Функція 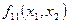 – імплікація; її позначення:
– імплікація; її позначення:  .
.
Функція  .
.
Функція  - імплікація; її позначення:
- імплікація; її позначення:  . Вона дорівнює 0 тільки тоді, коли
. Вона дорівнює 0 тільки тоді, коли  а
а  .
.
Функція  – штрих Шеффера або І-НІ (NAND); її позначення:
– штрих Шеффера або І-НІ (NAND); її позначення:  або
або  . Вона дорівнює 0 тоді й тільки тоді, коли обидва аргументи рівні 1.
. Вона дорівнює 0 тоді й тільки тоді, коли обидва аргументи рівні 1.
Реалізація функцій формулами
Суперпозицією функцій  називається функція
називається функція  отримана за допомогою підстановок цих функцій друг у друга й перейменування змінних. Формулою називається вираження, що описує суперпозицію функцій.
отримана за допомогою підстановок цих функцій друг у друга й перейменування змінних. Формулою називається вираження, що описує суперпозицію функцій.
Нехай дана множина (кінцевих або нескінченних) вихідних логічних функцій  . Всі формули, які містять тільки символи змінних, дужки й знаки функцій з множини
. Всі формули, які містять тільки символи змінних, дужки й знаки функцій з множини  , називаються формулами над
, називаються формулами над  .
.
Суперпозиція елементарних булевих функцій - формула.
Приклад: 
Таким чином, формула кожному набору значень аргументів ставить у відповідність значення функції й служить поряд з таблицею способом завдання й обчислення функції.
Формули, що представляють одну й ту саму функцію, називаються еквівалентними або рівносильними. Еквівалентність формул позначається знаком 
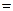 або
або  . Стандартний метод визначення еквівалентності двох формул полягає в наступному: по кожній формулі будується таблиця істинності функції, а потім отримані дві таблиці порівнюються. Інший метод називається методом еквівалентних перетворень і складається в перетворенні однієї з формул (або обох) до тих пір, поки не прийдемо до однакової форми.
. Стандартний метод визначення еквівалентності двох формул полягає в наступному: по кожній формулі будується таблиця істинності функції, а потім отримані дві таблиці порівнюються. Інший метод називається методом еквівалентних перетворень і складається в перетворенні однієї з формул (або обох) до тих пір, поки не прийдемо до однакової форми.
Нормальні форми булевих функцій.
Алгоритм приведення до ДДНФ і ДКНФ довільної логічної функції
Досконала диз'юнктивна й кон’юктивна нормальна форми дають спосіб подання булевої функції за допомогою суперпозиції кон’юнкції, диз'юнкції й заперечення, якщо в нас є таблиця значень функції.
Подання булевої функції у вигляді

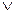

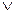
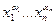 ,
,


де диз'юнкція береться по всім  , на яких
, на яких  , називається досконалою диз'юнктивною нормальною формою (ДДНФ). Усяка булева функція (крім 0) має єдину СДНФ.
, називається досконалою диз'юнктивною нормальною формою (ДДНФ). Усяка булева функція (крім 0) має єдину СДНФ.
Щоб одержати досконалу диз'юнктивну нормальну форму, треба взяти всі набори, на яких значення функції дорівнює 1 і записати для кожного з них кон’юнкцію змінних й їхніх заперечень. Якщо в наборі значення змінної 0 - то змінну треба взяти із запереченням, якщо 1 - без заперечення. З наборів кон’юнкцій змінних треба побудувати диз'юнкцію.
Приклад 1. (Досконала диз'юнктивна нормальна форма).
Побудуємо досконалу диз'юнктивну нормальну форму функції, заданою наступною табл. 2.
Таблиця 2
Функція задана за допомогою таблиці.
| x | y | z | f |
Набори, на яких функція дорівнює 1 – це (0,1,1), (1,0,1), (1,1,0), (1,1,1). Перший набір дає кон’юнкцію x & y & z, другий – x & y & z, третій – x & y & четвертий – x & y & z.
У результаті одержуємо (x & y & z) √ (x & y & z) √ (x & y & z√ (x&y&z).
Щоб одержати досконалу кон’юктивну нормальну форму, треба взяти всі набори, на яких значення функції дорівнює 0 і записати для кожного з них диз'юнкцію змінних й їхніх заперечень. Якщо в наборі значення змінної 0 - то змінну треба взяти без заперечення, якщо 1 - із запереченням. З диз'юнкцій, що вийшли, треба побудувати кон’юнкцію.
Контрольні питання:
1. Які функції двох змінних ви знаєте?
2. Як представити функцію у ДДНФ?
3. Як представити функцію у СДНФ?
ПЕРЕЛІК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ:
1. Редькин Н.П.: Дискретная математика. М.: Лань-2006г., 96стр.
2. Белоусов А.И., Ткачёв С.Б.: Дискретная математика. М.: МГТУ им. Н.Э. Баумана-2004г., 742 стр.
3. Аляев Ю.А., Тюрин С.Ф.: Дискретная математика и математическая логика. М.: n/a-2006г., 366 стр.
4. Новиков Ф.А.: Дискретная математика для программистов. 2-е издание. С.-П.: Питер-2006г., 368стр.
5. Гаврилов Г.П., Сапоженко А.А.: Задачи и упражнения по дискретной математике: Учеб. пособие – 3-е изд. М.: ФИЗМАТЛИТ-2005г.,
416 стр.
6. Хаггарти Р.: Дискретная математика для программистов.
М.: Техносфера-2003г., 320стр.
Додаток А
Таблиця 1
Варіанти завдань до лабораторних робіт 6 та 7
| №в | 10à Р Лабораторна робота 6 | Рà 10 Лабораторна робота 7 | ||
| Вхідне число | Основа системи | Основа системи | Число для перекладу | |
| 1526,256 2354,689 1243,658 7894,2658 4532,6872 1234,553 123,45687 4567,6488 3642,4568 7541,369 4164,1236 9431,7856 234,24658 4586,136 1646,4593 6666,48563 1254,6978 236,5498 1255,85 2136,4567 1234,2465 782,3465 4568,9645 4636,356 4865,365 2456,246 123,5468 346,26579 2459,356 1247,3568 8645,3269 3274,356 4258,369 654,32158 4236,2358 4876,2435 7894,3654 3214,6589 5794,3658 4589,2367 3549,9578 9864,6785 3869,4785 4975,6894 3456,75 465,7892 453,2687 425,3679 7745,35647 5789,23465 3256,4258 4895,3264 4587,3562 7895,4356 4259,365 4863,656 4569,32 365,458 12,35648 1234,67895 123,4568 652,36589 3256,9665 4867,34569 466,32648 456,325 6489,2436 1256,3654 9876,3468 256,3589 457,3311269 456,1287 3289,4561 7531,648 7913,4689 4571,7894 1246,3758 4596,136 4873,46981 245,4688 4695,12346 7921,463 4581,5544 7894,3265 7894,12365 4874,649 445,6523 123,4965 1785,549 4876,45 789,3465 945,468 1234,6357 1486,369 963,8756 9875,3684 8794,635 7943,1258 | 7896,35786 201546,8546 010101,1011 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 100011,1101 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 78A31,5786 B789,134256 A1326,42578 A123,45789 478913,45B AF86,25DC 4587,1292 D49,48793 7896,35786 201546,F546 11001,10110 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 789A31,5786 421B9,134256 74C26,42578 B123,45A 478913,45A9 AG86G,25DC 4587,1292 7849,48793 7896,G786 201546,854 01011,1010 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 7896431,5786 4216789,134256 7451326,42578 123,45789 478913,45789 AFG6G,25DC 4587,1292045 7849,48793 7896.35786 201546.8546 1101101,011 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 7896431,5786 4216789,134256 7451326,42578 123,45789 478913,45789 BC86G,25FA 4587,1292045 7849,48793 7896,35786 201546,8546 1110111,1111 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 7896431,5786 4216789,134256 7451326,42578 123,45789 478913,45789 12FG86G,D23C 4587,1292045 7849,48793 |
Таблиця 2
Варіанти завдань до лабораторної роботи 8
| №в | 2à 8, 2à 16 або 10à ДДК | 8à 2, 16à 2 або ДДКà10 | ||
| Вхідне число | Основа системи | Основа системи | Число для перекладу | |
| 111001,111101 111001,111101 1243,658 101110101,0101 10110101,1101 1234,553 1011101,0101 111111111111,111 723,568 11000111,11101 1111100000,010101 9431,7856 010101010,10101 1111010,001010 1646,4593 111110001010,01 1010100011,0101 236,5498 11010101,101111 1101111010,01 1234,2465 1010101,01011 11011,01 4636,356 1110111,0101 10101,000111111 346,26579 101011111,00001 10000000000,0001 8645,3269 11011,0001111 10111111,0101 654,32158 1010,01010 11,00001111111 7894,3654 1111011111,01 101101,000110 3549,9578 1011,010111 111111111,111111 3456,75 1000011110,0101 1110,0101 7745,35 11101,0101 10000100000,011 4895,32 101011011,0101 01010,1011 4863,656 10100000,010001 1110111,11111 12,356 1111100001,01 111011111,011111 652,36589 1110110,010 101001001001,0101 466,32648 1110000,0101 1110,1111101 1256,3654 101010010,011 001011001,1101 456,258 1011101,0101 111111111111,111 723,568 11000111,11101 1111100000,010101 9431,7856 010101010,10101 1111010,001010 1646,4593 111110001010,01 101110101,0101 125,2567 10110101,1101 10101000000,01 1234,553 1011101,0101 111111111111,111 723,568 11000111,11101 1111100000,010101 9431,7856 010101010,10101 1111010,001010 1646,4593 111110001010,01 1010100011,0101457,33 10101,101101 11111,11 10101111,01111 3289,4561 1110100001100,101 1110,111111 | ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК | ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК ДДК | 145,56 100011,001101 210210,2001 3120,12310 1000010,1 451224,125 1453,12346 110011000,010101 87631,24567 7896431,5786 1110001,10001 7451326,42578 123,45789 101110.1001 478913,45789 Af86G,25DC 101110101,0101 7849,48793 7896,35786 11001,101010 210210,2001 3120,12310 101110100001,0101 51324,12435 1453,12346 10100110101,0101 117456,10124 87631,24567 101110101,0101 4216789,134256 7451326,42578 10101,00011 478913,45789 AG86G,25DC 1010101,0001101 4587,1292045 7849,48793 10010101010101,01 7896,35786 201546.854 0101001,100101 210210,2001 3120,12310 1000010,1 451224,125 1453,12346 110011000,010101 87631,24567 7896431,5786 1110001,10001 7451326,42578 123,45789 101110.1001 478913,45789 Af86G,25DC 101110101,0101 7849,48793 7896,35786 11001,101010 210210,2001 3120,12310 110100101,011 210210,2001 3120,12310 42130,124 451324,12435 1453,12346 117456,10124 87631,24567 7896431,5786 4216789,134256 7451326,42578 123,45789 478913,45789 BC86G,25FA 4587,1292045 7849,48793 7896.35786 201546.8546 1110111,1111 210210,2001 3120,12310 1110001,10001 7451326,42578 123,45789 101110.1001 478913,45789 Af86G,25DC 101110101,0101 7849,48793 7896,35786 11001,101010 210210,2001 3120,12310 101110100001,0101 51324,12435 1453,12346 10100110101,0101 |
Таблиця 3
Варіанти завдань до лабораторних робіт 9-10
| №в | Лабораторна робота №9 | Лабораторна робота №10 |
| Спосіб завдання універсальної множини | Математичний вираз | |
| ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0...255 Букви англ. алфавіту Букви російського алфавіту ASCI код Цілі числа 0…255 | (А  В) В)  C\(А C\(А  C)
(А C)
(А  В)\(C В)\(C  B\А)
А\B B\А)
А\B  (C\B\А)
А (C\B\А)
А  В В  С С  А\(А А\(А  В)
А В)
А  (B\C)\(А (B\C)\(А  В)\(А В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
C C
C  B\B B\B  (C\A)
B\C\A(C (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A\(A A\(A  C C  B)
(А B)
(А  В) Δ C\(А В) Δ C\(А  C)
(А C)
(А  В)\(C В)\(C  B Δ А)
А\B B Δ А)
А\B  (C\B\А)
А (C\B\А)
А  В Δ C В Δ C  А\(А А\(А  В)
С В)
С  А А  В\А В\А  (А\C) А Δ (B\C)\(А (А\C) А Δ (B\C)\(А  В)\(А В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B Δ C B Δ C  A A  B B  C
C C
C  B\B B\B  (C\A)
B\C\A(C Δ B (C\A)
B\C\A(C Δ B  A)
C A)
C  B B  A\(A A\(A  C Δ B)
(А C Δ B)
(А  В) В)  C\(А C\(А  C)
А\B C)
А\B  (C\B\А)
А (C\B\А)
А  В В  С С  А\(А А\(А  В)
С В)
С  А А  В\А В\А  (А\C) А (А\C) А  (B\C)\(А Δ В)\(А (B\C)\(А Δ В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
C C
C  B\B Δ (C\A)
B\C\A(C B\B Δ (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A Δ (A A Δ (A  C C  B)
(А B)
(А  В) В)  C\(А C\(А  C)
(А C)
(А  В)\(C В)\(C  B\А)
А\B Δ (C\B\А)
А B\А)
А\B Δ (C\B\А)
А  В В  С С  А\(А А\(А  В)
С В)
С  А А  В\А В\А  (А\C) А (А\C) А  (B\C)\(А Δ В)\(А (B\C)\(А Δ В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
C C
C  B\B B\B  (C\A)
B\C\A(C (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A\(A Δ C A\(A Δ C  B)
(А B)
(А  В) В)  C\(А C\(А  C)
(А C)
(А  В)\(C В)\(C  B\А)
А\B B\А)
А\B  (C\B\А)
А (C\B\А)
А  В Δ C В Δ C  А\(А А\(А  В)
С В)
С  А А  В\А В\А  (А\C) А (А\C) А  (B\C)\(А (B\C)\(А  В)\(А В)\(А  C)
А Δ B\C C)
А Δ B\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C Δ A B\C Δ A  B B  C
C C
C  B\B B\B  (C\A)
B\C\A(C (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A\(A A\(A  C C  B)
(А B)
(А  В) В)  C\(А C\(А  C)
(А C)
(А  В) \(C В) \(C  B\А)
А\B Δ (C\B\А)
А B\А)
А\B Δ (C\B\А)
А  В В  С С  А\(А А\(А  В)
С В)
С  А А  В Δ А В Δ А  (А\C) А (А\C) А  (B\C)\(А (B\C)\(А  В)\(А В)\(А  C)
А C)
А  В\ C В\ C  (B \I)
CΔB (B \I)
CΔB  (A Δ C) (A Δ C)  B
A B
A  B \C B \C  A A  B B  C
C C
C  B\ B B\ B  (C\A)
B\C\A(C (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A\(A A\(A  C C  B)
(А B)
(А  В) В)  C\(А C\(А  C)
(А Δ ВC) C)
(А Δ ВC)  B\А)
А\B B\А)
А\B  (C\B\А)
А (C\B\А)
А  В В  С С  А\(А А\(А  В)
C Δ А В)
C Δ А  В\А В\А  (А\C) А (А\C) А  (B\C)\(А (B\C)\(А  В)\(А В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
А C
А  (B\C)\(А Δ В)\(А (B\C)\(А Δ В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
C C
C  B\B Δ (C\A)
B\C\A(C B\B Δ (C\A)
B\C\A(C  B B  A)
C A)
C  B B  A Δ (A A Δ (A  C C  B)
(А B)
(А  В) В)  C\(А C\(А  C)
(А C)
(А  В)\(C В)\(C  B\А)
А\B Δ (C\B\А)
А B\А)
А\B Δ (C\B\А)
А  В В  С С  А\(А А\(А  В)
С В)
С  А А  В\А В\А  (А\C) А (А\C) А  (B\C)\(А Δ В)\(А (B\C)\(А Δ В)\(А  C)
А C)
А  В\C В\C  (B\I)
А (B\I)
А  (B\C)\(А Δ В)\(А (B\C)\(А Δ В)\(А  C)
А C)
А  В\C В\C  (B\I)
C (B\I)
C  B B  (A (A  C) C)  B
A B
A  B\C B\C  A A  B B  C
C C
C  B\B Δ (C\A) B\B Δ (C\A)
|
 - перетинання \ - різниця
- перетинання \ - різниця
Δ – симетрична різниця  - об'єднання
- об'єднання
A - заперечення множини А
Таблиця 4
Варіанти завдань до лабораторної роботи 11
| N | Функція 
| N | Функція 
|
 
| 
| ||
 
| 
| ||

|  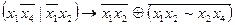
| ||

|  
| ||

| 
| ||

| 
| ||

| 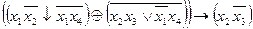
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
|
|
|
|
|
|
Дата добавления: 2016-11-18; Мы поможем в написании ваших работ!; просмотров: 944 | Нарушение авторских прав
Лучшие изречения:






