Статистична обробка експериментальних даних в Excel

1.5.1 Мета і завдання роботи

Вміти застосувати електронні таблиці Excel для проведення первинної статистичної обробки, використовуючи статистичні функції.

Тривалість роботи – 2 год

1.5.2 Основні теоретичні положення

Зараз в процесі обробки та інтерпретації даних суттєвого значення набувають ймовірнісно-статистичні методи аналізу. Дані, що отримані в окремих точках спостережень, варто розглядати як випадкові події. Теорія ймовірностей вивчає закономірності випадкових подій у часі та просторі і прийоми їх кількісного опису.

Аналіз даних проводиться із застосуванням методів математичної статистики, яка дає можливість вивести оцінки характеристик випадкової величини серед яких використовуються: числові характеристики; характеристики розподілу; характеристики взаємозв’язку.

До основних числових характеристик відносяться: математичне очікування (середнє арифметичне), мода, медіана, дисперсія, середньоквадратичне відхилення, коефіцієнт варіації, асиметрія, ексцес. Розрахувати перераховані статистичні характеристики можна за допомогою зазначених нижче формул, так і статистичних функцій Excel.

Якщо виміри виконані в одинакових умовах, тобто рівноточні, то центр групування результатів таких вимірів визначається середнім арифметичним ()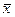

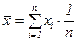(1)

функція Excel – СРЗНАЧ(число1; число2;…).

Мода - це найбільш ймовірне значення випадкової величини МОДА (число1; число2;…).

Медіана - таке значення випадкової величини відносно якого одинаково ймовірно прояв випадкової величини більше або менше цього значення МЕДИАНА (число1; число2;…).

Дисперсія (s²) – це математичне очікування квадрату відхилення випадкової величини від її математичного відхилення ДИСП(число1; число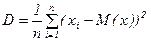2;…)

(2)

Середньоквадратичне відхилення s - міра розсіювання окремих даних навколо середнього арифметичного. СТАНДОТКЛОН(число1; число2;…)

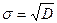(3)

Коефіцієнт асиметрії – характеризує ступінь несиметричності розподілу відносно середнього. Додатня асиметрія вказує на відхилення розподілу в бік додатніх значень, від’ємна асиметрія вказує на відхилення розподілу в бік від’ємних значень. СКОС(число1; число2;…)

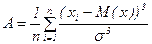(4)

Коефіцієнт ексцесу - характеризує відносну гостроту або згладженість розподілу порівняно з нормальним розподілом. Додатній ексцес означає відносно гострокіневий розподіл, від’ємний – відносно згладжений розподіл. ЭКСЦЕСС(число1; число2;…).

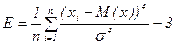(5)

Для всіх перерахованих функцій кількість аргументів обмежена до 30.

Якщо об’єм вибірки невеликий (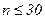), то за розрахованими значеннями коефіцієнтів асиметрії та ексцесу можна судити про нормальність розподілу, для іншого розподілу статистичні оцінки можуть бути несправедливими. Будь-які параметри вибірки, в тому числі асиметрія та ексцес є випадковими аеличинами, отже навіть для нормального розподілу можуть відрізнятись від нуля. Розраховують емпіричні дисперсії асиметрії та ексцесу:

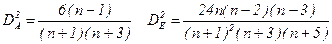(6)

За такими дисперсіями можна оцінити, чи суттєво вибіркові асиметрія та ексцес відхиляються від своїх маткматичних очікувань, тобто від нуля. Якщо

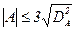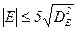і (7),

то робимо висновок, що спостережений розподіл нормальний, в протилежному випадку гіпотезу нормальності варто відкинути або вважвти сумнівною.

Гістограма – спрощена модель кривої густини розподілу випадкової величини. Побудувавши її та порівнявши з еталонними графіками основних законів, можна приблизно судити про ступінь подібності між ними. Для побудови гістограми значення випадкової величини розбивають на визначене число розрядів (інтервалів групування) і підраховують, скільки їх попадає в кожний розряд. Потім по осі абсцис відкладають розряди, а по осі ординат - відповідні їм частоти В переважній більшості випадків оптимальний крок інтервалу групування 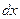розраховується за формулою Стерджеса:

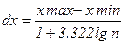, (8)

де 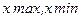- максимальне і мінімальне значення ознаки;

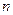- об’єм вибірки.

Отриманий результат необхідно округлити до цілого числа.

Якщо гістограма симетрична відносно вертикальної осі, яка проходить через її вершину, то можна говорити про можливість нормального закону розподілу. За виглядом побудованої гістограми можна судити про ступінь відхилення від нормального розподілу.

Перевіряючи гіпотезу про відповідність фактичного закону розподілу ознаки нормальному, ми можемо її прийняти, відкинути або прийти до висновку, що для прийняття рішення недостатньо даних. Гіпотеза може бути прийнята як правильна за рівнем значимості і позначають a. Величина a вибирається досить малою за принципом практичної неможливості малоймовірних подій. В основному приймають для a одне значення: 0.05. ДОВЕРИТ(альфа; середньоквадратичне відхилення; розмір вибірки).

Коефіцієнт кореляції Пірсона між двома змінними дорівнює коваріації двох змінних, або сумі добутків відхилень, поділеній на добуток їх стандартних відхилень. Нехай, є дві вибірки 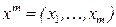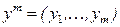. Коефіцієнт кореляції Пірсона розраховується за формулою:

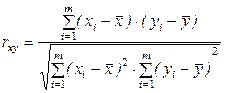, (9)

де 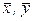– вибіркові середні, .

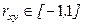Коефіцієнт кореляції набуває значень від -1 до 1. Значення “+1” означає, що залежність між X та Y є лінійною, і всі точки функції лежать на прямій, яка відображає зростання Y при зростанні X. Значення “-1” означає, що всі точки лежать на прямій, яка відображає зменшення Y при зростанні X. Якщо коефіцієнт кореляції Пірсона = 0, то лінійної кореляції між змінними немає.

 

Порядок виконання роботи

1. Використовуючи відповідні функції Excel виконати розрахунки основних числових статистичних характеристик (дані взяти з таблиці 3 згідно варіанту).

2. Побудувати гістограму, перевірити гіпотезу про нормальний закон розподілу за показниками асиметрії, ексцесу. Для побудови гістограми можна використовувати пакет аналізу Excel. Щоб ввімкнути пакет аналізу необхідно ввімкнути цю опцію в меню Сервіс-Надстройки. Після цього команда Аналіз даних з’явиться в цьому ж меню.

3. На окремому листі, використовуючи команду Аналіз даних побудувати матрицю коефіцієнтів кореляції (дані взяти з таблиці з варіантами).

 

1.5.4 Аналіз результатів роботи, висновки

У результаті виконання даної роботи студенти набувають практичних навиків у застосуванні вбудованих статистичних функцій Excel для обчислень основних статистичних характеристик, побудови гістограми та перевірки закону розподілу випадкової величини за показниками асиметрії та ексцесу.

 

1.5.5 Контрольні запитання

1. Які Ви знаєте основні числові статистичні характеристики? Назвіть відповідні функції Excel.

2. Що таке рівень значимості, за якою функцією він розраховується?

3. Як перевірити нормальність розподілу за показниками асиметрії, ексцесу?

4. Що таке коефіцієнт кореляції? Функція Excel.

5. Як оцінити характер і ступінь парного зв’язку між двома незалежними величинами?

 

1.5.6 Рекомендована література

1 Баженов В.А. і ін. Інформатика. Комп’ютерна техніка. Комп’ютерні технології: Підручник. – К.: Каравела, 2003. – 464 с.

2 Основы информатики. Учебное пособие. Издание 2 – е, переработанное и дополненное. – М.: Информационно-издательский дом “Филинъ”, 1999. - 544 с.

3 Інформатика. Комп’ютерна техніка. Комп’ютерні технології.: Підручник/Пушкар О.І., ред.-К.:Академія,2002.–704 с.

Таблиця 3- Вихідні дані до лабораторної роботи для варіантів 1 – 11

 

ч/ч	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10	Х11
	2,7				1,6	1,5		15,9	2,3
	2,6				1,7	1,8		13,3	1,7
	2,6				1,8	3,1		5,7	1,9
	2,7				2,1	4,1		16,1	2,1
	2,7				2,0	1,9		26,6	2,5
	2,8				1,7	2,5		3,1	2,2
	2,6				1,9	3,5		2,8	2,0
	2,7				1,6	3,3		10,7	2,0
	2,7				1,7	1,6		2,4	1,7
	2,7				1,6	2,9		-8,6	1,8
	2,6				2,2	2,8		13,7	2,0
	2,7				2,1	3,0		19,5	2,0
	2,6				1,8	3,0		10,8	2,0
	2,7				1,8	4,6		18,1	2,4
	2,6				1,8	2,9		25,0	2,1
	2,6				1,7	2,8		22,5	2,2
	2,6				1,8	3,7		11,4	1,9
	2,8				1,7	4,1		19,3	1,7
	2,6				1,9	4,2		13,1	1,8
	2,7				2,1	2,1		17,2	2,0
	2,7				2,2	1,7		13,1	1,8
	2,7				2,1	4,1		11,7	2,5
	2,7				1,8	1,9		16,1	1,6
	2,6				1,8	2,5		15,3	1,9
	2,6				1,8	3,5		13,9	2,0
	2,7				1,8	3,3		14,0	1,7
	2,6				2,1	1,8		21,0	1,8
	2,7				2,0	2,9		32,0	1,7

 

Продовження таблиці 3- Вихідні дані до лабораторної роботи для варіантів 12 - 22

 

ч/ч	Х12	Х13	Х14	Х15	Х165	Х176	Х187	Х1998	Х20	Х21	Х22
		1,5	32,9	1,2	19,3	-74,2			12,8	71,0	15,5
		1,5	32,8	1,5	20,4	-61,7			16,2	80,2	16,4
		1,5	30,4	1,3	25,8	-41,6			18,8	77,3	12,7
		1,6	11,6	1,3	27,6	-21,6			16,5	71,6	11,5
		1,6	30,6	1,3	44,1	-18,6			19,3	78,3	15,0
		1,5	34,4	1,4	21,6	-17,6			15,7	70,3	18,4
		1,6	22,6	1,4	42,1	-14,6			14,8	66,7	17,8
		1,6	34,2	1,5	19,6	-15,6			19,7	80,3	20,6
		1,7	29,2	1,5	36,1	-16,1			24,5	69,4	19,7
		1,7	29,2	1,8	34,2	-14,1			19,5	72,0	15,3
		1,7	31,8	1,7	14,8	-10,6			10,7	75,4	17,7
		1,8	10,9	1,8	44,6	-7,4			24,8	83,2	8,1
		1,8	32,0	1,9	19,7	6,2			9,7	70,5	12,0
		1,8	18,8	2,0	20,5	6,1			14,0	70,1	9,4
		1,9	13,4	2,0	38,7	-7,6			18,7	72,3	15,0
		1,8	32,9	2,1	34,1	-4,2			15,5	72,4	16,3
		1,9	26,8	2,2	21,6	5,2			13,1	74,5	8,6
		1,9	26,8	2,2	18,2	4,1			12,4	68,9	12,0
		2,0	33,1	2,3	19,6	-4,7			18,2	82,6	15,6
		1,9	25,0	2,4	37,2	5,6			14,2	68,1	8,7
		2,1	28,4	2,2	38,6	3,1			14,1	69,3	13,6
		2,3	24,9	2,1	25,3	-4,5			15,7	70,3	17,7
		2,2	5,3	1,9	14,5	-6,7			14,8	66,7	8,1
		2,3	28,4	2,3	19,6	-7,5			19,7	80,3	10,0
		2,0	21,9	2,7	9,6	6,4			24,5	69,4	15,0
		1,8	16,6	3,1	9,4	11,2			19,5	72,0	18,4
		2,1	18,6	4,1	16,1	12,4			10,7	75,4	17,8
		1,7	13,5	4,2	9,2	18,6			18,7	72,3	20,6