Биофизика мышечного сокращения

Жизнедеятельность человека, животных, птиц, рыб, растений и других биологических объектов неразрывно связана с механическими движениями (перемещениями). Все виды движения в биообъектах можно разделить на две группы: макродвижения и микродвижения. К макродвижениям следует отнести: различные виды телодвижений, кровообращение, дыхание. К микродвижениям относят транспорт веществ через мембраны, колебательные, циркуляционные и фонтанирующие движения цитоплазмы, водно-электролитный обмен в капиллярных сосудах и другие микропроцессы в клетках, тканях и органах. Макродвижения осуществляются благодаря наличию мышечных образований (мышц), обладающих специальным белковым сократительным комплексом - актомиозином. На происхождение микродвижений до сих пор нет единой точки зрения, однако наиболее вероятной считается гипотеза функционирования сократительных элементов, подобных мышечным. Из приведенного краткого обзора видна огромная роль изучения механизма работы мышц, как одного из основных форм существования живой материи. Кроме того, знание сущности мышечного сокращения заключается и в том, что изучение прямого превращения химической энергии в механическую, без промежуточного превращения ее в тепловую или электрическую энергию, представляет большой технический интерес, открывая перспективы создания нового типа двигателей с достаточно большим коэффициентом полезного действия. В настоящей лекции рассматривается структура и функция скелетных мышц, их качественное и количественное описание. Гладкомышечные образования имеют свою специфику сократительной деятельности, макродвижения еще недостаточно изучены и в данной лекции эти вопросы не отражены.

Скелетная мышца позвоночных состоит из нескольких тысяч параллельных мышечных волокон диаметром (1СМ-1ОО мкм), заключенных в общую оболочку. Волокна на каждом конце мышцы переходят в сухожилия, которые закреплены на костной ткани, являются абсолютно упругими элементами и воспринимают напряжение при сокращении мышцы. Через концевую пластинку каждого мышечного волокна присоединяются окончания нервных волокон. Нервный импульс от ЦНС приводит к раздражению группы мышечных волокон(двигательных единиц). Мышечное волокно, в свою очередь, содержит от 1000 до 2000 параллельных нитей (миофибрилл), диаметром около 1 мкм. Весь пучок миофибрилл заключен в мембране — плазмолемме. Плазмолемма, подобно мембранам других клеток, состоит из трех слоев белков и липидов, общей толщиной около 10 нм и электрически поляризована. Сверху плазмолемма покрыта тонким слоем коллагеновых нитей, обладающих упругими свойствами. Кроме миофибрилл в мышечном волокне содержится много ядер, расположенных вблизи плазмолеммы, и большое количество митохондрий, находящихся между миофибриллами. Ядра состоят из трубочек и пузырьков (цитоплазматический ретикулум), которые выделяют кальций при возбуждении мышечного волокна и удаляют его из саркоплазмы при прекращении мышечного возбуждения. Митохондрии являются центральными образованиями макроэргических соединений, прежде всего АТФ. Молекулы АТФ поступают из митохондрий через саркоплазму к миофибриллам в момент сокращения. Основной надмолекулярной двигательной структурой мышечных волокон является саркомер. Саркомеры расположены в мышечном волокне последовательно один за другим.

Каждый саркомер ограничен Z - пластинками. Между ними находятся тонкие нити, составленные из молекул белка F-актина, и толстые нити, образованные молекулами белка миозина. Нити имеют гексагональную упаковку, так, что каждая толстая нить взаимодействует с 6-ю тонкими нитями, а каждая тонкая нить взаимодействует с 3-мя толстыми нитями. Тонкая нить имеет структуру двойной суперспирали (3), а каждая спираль состоит из глобулы белка G-актина. Глобула - это пространственное расположение полимерной нити, при которой отдельные звенья имеют определенную пространственную структуру и расположение. Толстые нити также на 50 % состоят из двойной α - спирали молекул миозина, однако, в толстой нити имеются так называемые "шарнирные" участки, где в суперспираль встроены глобулярные головки, расположенные радиально к оси толстой нити. Эти головки расположены по обе стороны толстой нити (их называют мостиками). Два смежных мостика располагаются под углом 120° друг к другу; так что участок из 4 мостиков является повторяющимся элементом и имеет длину 43 нм. Сокращение (укорочение) мышечного волокна происходит за счет уменьшения длины саркомеров по следующей схеме. При раздражении мышечного волокна нервным импульсом, из саркоплазматического ретикулума поступают ионы кальция, которые активизируют определенные микроучастки тонких нитей, в результате этого актиновые центры становятся доступными для взаимодействия с миозиновыми мостиками. Структура миозиновой нити не изменяется, а миозиновые мостики изменяют свое направление (наклоняются влево) и проталкивают толстую нить ближе к Z - пластинке, а возбужденная область тонких нитей смещается на один шаг вправо. Такая кинематика движений надмолекулярных структур при укорочении мышцы называется схемой скользящих нитей. Взаимодействие миозиновых мостиков и актиновых нитей происходит за счет энергии АТФ, находящейся в митохондриях, в присутствии ионов кальция. Значение силы, развиваемой мышцей при изометрическом сокращении, зависит от длины саркомера, т.е. от степени перекрытия нитей:

- в покоящейся мышце мостики не взаимодействуют с тонкой нитью и такая мышца легко растяжима, развиваемая сила очень мала (до положения 1).

- до положения 2 количество взаимодействующих мостиков увеличивается, и сила, развиваемая мышцей, возрастает линейно до максимального значения.

- от положения 2 до положения 5 сила взаимодействия изменяется незначительно, т.к. количество взаимодействующих мостиков практически не изменяется.

- от положения 5 до положения 6 сила взаимодействия уменьшается практически до нуля, т.к. дальнейшее уменьшение саркомера приводит к торможению скольжения нитей и к деформациям толстых и тонких нитей.

Таким образом, зависимость сил сокращения мышц от длины саркомера можно разделить на 2 части: первая часть от положения 1 до положения 2 - называется рабочим циклом, и последняя часть от положения 5 до положения 6 - холостым циклом. Это подобно двухтактному двигателю внутреннего сгорания. Следует отметить также, что возбуждение группы мышечных волокон может осуществляться от одного нервного волокна, в этом случае нервное волокно разветвляется на несколько синапсов. Совокупность мышечных волокон, которые одномоментно возбуждаются (иннервируются) от одного нервного волокна, называется двигательной единицей. Различные двигательные единицы "разряжаются" (сокращаются) не одномоментно, а хаотически, этим поддерживается постоянный тонус скелетной мышцы.

По своим механическим свойствам мышцы относятся к эластомерам - материалам, обладающим значительной растяжимостью и упругостью.

Величина механического напряжения σ, возникающего при сокращении мышцы прямо пропорциональна относительной деформации, согласно закону Гука.

σ = F/S - механическое напряжение, F - развиваемая сила, S - площадь поперечного сечения; ε = Δ L/L₀ - относительная деформация, L -первоначальная длина, L₀ - абсолютная деформация (удлинение); Е - модуль упругости (модуль Юнга). Он определяется величиной механического напряжения в сокращенной мышце, при увеличении ее длинны в два раза. По своим упругим свойствам и механизму деформации, мышечное волокно близко к каучуку: модуль упругости для обоих материалов равен 10⁶ Па. При сильном напряжении как в мышце, так и в каучуке, наблюдается локальная кристаллизация (упорядочение макромолекулярной белковой структуры фибриллярного типа). Однако, при слабом и среднем сокращении, восстановление не бывает полным. Наличие остаточных деформаций характеризует пластичность мышцы - способность не сохранять свою форму и размеры, после прекращения действия силы. Таким образом, мышца не является абсолютно упругим телом, а обладает вязкоупругими свойствами. При очень сильном растяжении мышца ведет себя как нормально упругое тело. В этом случае температура мышцы понижается за счет локальной кристаллизации. При сокращении мышцы развивается напряжение и совершается работа. Мышца обладает сократительными и эластичными элементами, поэтому возникающее напряжение и совершаемая работа обусловлены не только активным сокращением сократительного комплекса, но и пассивным сокращением, определяемым эластичностью или так называемым последовательным упругим компонентом мышцы. За счет последовательного упругого компонента совершается работа только в том случае, если мышца была предварительно растянута, а величина этой работы пропорциональна величине растяжения. Этим, в большей степени, объясняется то, что наиболее мощные движения совершаются при большой амплитуде, обеспечивающей предварительное растяжение мышц.

Мышечные сокращения делятся на изометрические - происходящие при неизменной длине мышцы, и изотонические - происходящие при неизменном напряжении. В организме сокращения мышц никогда не бывают чисто изометрическими или чисто изотоническими. Скелетные мышцы, с помощью сухожилий, прикрепляются к костям, которые образуют систему рычагов. Плечо рычага мышцы, в большинстве случаев, бывает меньше плеча рычага соответствующей кости. Согласно Аккерману, механический выигрыш в амплитуде движений человека имеет величину от 2,5 до 20. Для двуглавой мышцы плеча он равен 10. В зависимости от силы, которую развивает мышца, скорость сокращения (укорочения) мышцы бывает различной. Хилл, на основе опытных данных, при работе на изолированных мышцах, вывел так называемое основное уравнение сокращения мышцы. Согласно этого уравнения, скорость сокращения мышцы находится в гиперболической зависимости от величины нагрузки F.

(F + а) * (υ + b) = const, где а и b - константы, равные соответственно 1/4 F и 1/4υ.

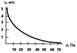
Байером были сделаны замечания к уравнению Хилла, которые приводят уравнение Хилла к следующему виду: F`υ` = const

Произведение F`υ` представляет собой общую мощность, развиваемую мышцей при сокращении. Так как F меньше F`υ`, т.е. внешняя мощность меньше общей мощности, то следует предположить, что мышца совершает не только внешнюю работу, но еще и как бы увеличивается на величину a, а скорость сокращения - на величину b. Эту внутреннюю работу можно оценивать как потерю энергии на внутреннее трение в форме теплового рассеяния. Тогда можно отметить, что общая мощность мышцы, в физиологических пределах, является величиной постоянной, не зависящей от величины нагрузки и скорости сокращения. С термодинамической точки зрения, мышца представляет собой систему, которая преобразует энергию химических связей (энергию АТФ) в механическую работу, т.е. мышца является хемомеханической машиной. Как уже отмечалось, при сокращении мышцы происходит теплообразование. Хиллом, с помощью термоэлектрических методов, было установлено, что при каждом раздражении в начале выделяется постоянная по величине и независящая от нагрузки теплота активации Q, а затем теплота сокращения kAL, пропорциональная сокращению мышцы AL и независящая от нагрузки (k - коэффициент пропорциональности). Если сокращение изотоническое, то мышца производит работу А, равную произведению нагрузки F на величину сокращения:

A = FAL

Согласно первому закону термодинамики, изменение внутренней энергии ΔU мышцы будет равняться сумме выделенного тепла и совершенной работы:

ΔU = Q + kΔL + FΔL или ΔU = Q + (k +F)ΔL

КПД = A/ΔU или КПД =(FΔL)/(Q + (k + F)ΔL

Учитывая, что величины Q и к не зависят от F, из уравнения следует, что, в определенных пределах, КПД мышечного сокращения будет увеличиваться при увеличении нагрузки. Хилл, на основании полученных им в опытах данных, определил, что КПД мышечного сокращения примерно равен 40%. Величина КПД 40% показывает эффективность превращения энергии АТФ в механическую энергию.