Программирование алгоритмов с использованием подпрограмм

Цель работы

 

18.1.1 Составление программ с использованием подпрограмм - процедур, подпрограмм - функций

18.1.2 Отладка программы и контрольный просчет.

 

Приборы и оборудование

 

18.2.1 Free Pascal

18.2.2 ПЭВМ IBM PC/XT

18.2.3 Microsoft Word

18.2.4 Задание на выполнение работы в электронном варианте.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

18.3.1 Выберите номер варианта, согласно списка в учебном журнале (Приложение А).

18.3.2 Составьте программу, используя язык программирования Free Pascal

18.3.3 Составьте программу, с использованием подпрограмм - процедур, подпрограмм - функций

18.3.4 Отладить программу с использованием контрольного примера (значения переменных задайте сами).

18.3.5 Результаты работы распечатайте на принтере.

18.3.6 Оформите лабораторную работу для сдачи преподавателю

18.3.7 Ответьте на контрольные вопросы устно

Примечание:

- на одном и том же задании составить подпрограмму – процедуру и подпрограмму – функцию, задав одни и те же значения переменным данных процедур;

- написать программу обращения к данным процедурам

- получить один и тот же результат и сравнить данные процедуры, что у них обще, а в чем отличие;

Контрольные вопросы

 

18.4.1 Для чего нужны в программе процедуры и функции?

18.4.2 В чем отличие между процедурой и функцией?

18.4.3 Чем отличаются формальные и фактические параметры?

18.4.4 Чем отличаются параметры-значения и параметры-переменные?

18.4.5 Как объявляются глобальные и локальные переменные? Каково правило видимости этих переменных?

18.4.6 Почему при обращении к процедуре, аргумент, передаваемый параметру-переменной, может быть только переменной, а не константой или выражением?

 

Приложение А

Номер варианта	Выражение
	1.1 Треугольник задан координатами своих вершин. Составить программу для вычисления его площади 1.2 Описать функции Min2(A,B) и Max2(A,B)2 вещественного типа, находящие минимальное и максимальное из двух вещественных чисел A и B.
	2.1 Составить программу для нахождения наибольшего общего делителя четырех натуральных чисел. 2.2. Описать процедуру Minmax(A,B), записывающую в переменную A минимальное из значений A и B, а в переменную B - максимальное из этих значений
	3.1 Составить программу для нахождения наименьшего общего кратного трех натуральных чисел 3.2 Описать функцию Fact(N) целого типа, вычисляющую значение факториала N! = 1·2·...·N (N > 0 - параметр целого типа). С помощью этой функции вычислить факториалы 10 данных чисел.
	4.1 Написать программу для нахождения суммы большего и меньшего из трех чисел 4.2 Описать процедуру SumDigit(N,S), находящую сумму цифр S целого числа N (N - входной, S - выходной параметр). Используя эту процедуру, найти суммы цифр пяти данных чисел.
	5.1 Вычислить площадь правильного шестиугольника со стороной а, используя подпрограмму вычисления площади треугольника. 5.2 Описать функцию Polynom(A,N,X) вещественного типа, находящую значение полинома P в вещественной точке X. Полином P задается параметрами N (степень полинома, 0 < N < 8) и A (коэффициенты полинома, вещественный массив размера N+1): P(X) = A[1]·XN + A[2]·XN-1 +... + A[N]·X + A[N+1]. Используя эту функцию, найти значения заданного полинома в пяти данных точках.
	6.1. Составит программу, проверяющую, являются ли данные три числа взаимно простыми. 6.2 Описать функцию Min(A,N) и Max(A,N)2 вещественного типа, находящую минимальный и максимальный элемент массива A, состоящего из N вещественных чисел
	7.1 Написать программу для вычисления суммы факториалов всех нечетных чисел от 1 до 9. 7.2 Описать функцию NMin(A,N) и NMax(A,N)2 целого типа, находящую номер минимального и максимального2 элемента массива A (массив состоит из N вещественных чисел).
	8.1 Даны две дроби А/В и С/D (А, В, С, D – натуральные числа). Составить программу для деления дроби на дробь. Результат должен быть несократимой дробью 8.2 Описать процедуру NMinmax(A,N,NMin,NMax), находящую номера минимального и максимального элемента массива A из N вещественных чисел.
	9.1 Даны две дроби А/В и С/D (А, В, С, D – натуральные числа). Составить программу для умножения дроби на дробь. Результат должен быть несократимой дробью 9.2 Описать процедуру Invert(A,N), меняющую порядок следования элементов массива A из N вещественных чисел на противоположный ("инвертирование массива").
	10.1 Даны две дроби А/В и С/D (А, В, С, D – натуральные числа). Составить программу для вычитания из первой дроби второй. Результат должен быть несократимой дробью 10.2 Описать процедуру Smooth(A,N), заменяющую каждый элемент вещественного массива A размера N на его среднее арифметическое со своими соседями ("сглаживание массива"). С помощью этой процедуры выполнить пятикратное сглаживание данного массива A размера N, выводя на экран результаты каждого сглаживания.
	11.1 Даны две дроби А/В и С/D (А, В, С, D – натуральные числа). Составить программу для сложения этих дробей. Результат должен быть несократимой дробью 11.2 Описать функцию SumLine(A,M,N,k) вещественного типа, вычисляющую сумму элементов вещественной матрицы A размера M x N, расположенных в k-й строке (если [k > M]1|[k > N]2, то функция возвращает 0).
	12.1 Составить программу для вычисления суммы факториалов всех четных чисел от m до n. 12.2 Описать функцию SumCol(A,M,N,k)2 вещественного типа, вычисляющую сумму элементов вещественной матрицы A размера M x N, расположенных в k-й столбце (если [k > M]1|[k > N]2, то функция возвращает 0).
	13.1 Дано простое число. Составить функцию, которая будет находить следующее за ним простое число. 13.2 Описать функцию IsIdent(S) целого типа, проверяющую, является ли строка S допустимым идентификатором Паскаля. При утвердительном ответе возвращается 0. Если S является пустой строкой, то возвращается -1, если строка начинается с цифры, то возвращается -2. Если S содержит недопустимые символы, то возвращается номер первого недопустимого символа. Проверить с помощью этой функции пять данных строк.
	14.1 Составить процедуру для нахождения наименьшего нечетного натурального делителя k(k не равно 1) любого заданного натурального числа n. 14.2 Описать функцию FillStr(S,Len) строкового типа, возвращающую строку длины Len, заполненную повторяющимися копиями строки-шаблона S (последняя копия строки-шаблона может входить в результирующую строку частично).
	15.1 Составить программу, определяющую, в каком из данных двух чисел больше цифр. 15.2 Описать процедуру Trim(S), удаляющую в строке S начальные и конечные пробелы
	16.1 Заменить данное натуральное число на число, которое получается из исходного записью его цифр в обратном порядке (например, дано число 156, нужно получить 651). 16.2 Описать функцию PosLast(subS,S) целого типа, возвращающую номер позиции, с которой в строке S содержится последнее вхождение подстроки subS. Если в строке S отсутствуют подстроки subS, то функция возвращает 0.
	17.1 Даны два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей (кроме его самого) другого числа (например, числа 220 и 284). Найти все пары «дружественных чисел», которые не больше данного числа N. 17.2 Даны действительные числа х1, у1, х2, у2, …,х10, у10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (х1, у1), (х2, у2), …, (х10, у10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами.)
	18.1 Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Вывести все пары «близнецов» из отрезка [n,2n], где n – заданное натуральное число больше 2. 18.2 Даны действительные числа a, b, c, d, e - стороны пятиугольника. Найти площадь пятиугольника. (Определить процедуру вычисления площади треугольника по его сторонам.)
	19.1 Натуральное число, в записи которого n цифр, называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу Армстронга от 1 до k.. 19.2 Даны три символьные матрицы. a) ту матрицу, где есть хотя бы одна гласная - транспонировать; b) в той матрице, на главной диагонали которой все цифры, найти наименьшую и удалить соответствующую строку.
	20.1 Найти все простые натуральные числа, не превосходящие n, двоичная запись которых представляет собой палиндром, т.е. читается одинаково слева направо и справа налево. 20.2 Описать функцию Stepen (x,n) от вещественного x и целого n, вычисляющую (посредством умножения) величину xn, и использовать ee для вычисления b=2.7k+(a+1)-5.
	21.1 Найти все натуральные n – значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234,5789). 21.2 Даны отрезки a,b,c и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, напечатать площадь данного треугольника. Определить процедуру Plo(x,y,z), печатающую площадь треугольника со сторонами x,y и z, если такой треугольник существует.
	22.1 Найти все натуральные числа, не превосходящие заданного n, которые делятся на каждую из своих цифр. 22.2 Пусть процедура Socr(a,b,p,q) от целых параметров (b№0)приводит дробь к несократимому виду Описать данную процедуру и использовать ее для приведения дроби 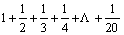к несократимому виду
	23.1 Составить программу для нахождения чисел из интервала [M,N], имеющих наибольшее количество делителей. 23.2 Даны длины a,b и c сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Длина медианы, проведенной к стороне a, равна
	24.1 Дано натуральное число n. Выяснить, можно ли представить его в виде произведения трех последовательных натуральных чисел. 24.2 Даны координаты вершин двух треугольников. Определить, какой из них имеет большую площадь.
	25.1 Имеется часть катушки с автобусными билетами. Номер билета шестизначный. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета - N, больший –M (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех). 25.2 Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найти расстояние от данной точки до ближайшей стороны треугольника. (При определении расстояний учесть, что площадь треугольника вычисляется и через три его стороны, и через основание и высоту.).
	26.1 Написать программу, определяющую сумму n –значных чисел, содержащих только нечетные числа. Определить также, сколько четных цифр в найденной сумме. 26.2 Три прямые на плоскости заданы уравнениями akx+bky=ck, k=1,2,3. Если эти прямые попарно пересекаются и образуют треугольник, тогда найти его площадь.
	27.1 Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т.д. Сколько таких действий надо произвести, чтобы получить нуль? 27.2 Два натуральных числа называются "дружественными", если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Напечатать все пары "дружественных" чисел, не превосходящих заданного натурального числа.
	28.1 Составить программу для разложения натурального числа на простые множители. Например, 200= 2³ *5² 28.2 Дано четное число n > 2. Проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел. Воспользоваться функцией распознавания простых чисел.
	29.1 Дано натуральное число n. Найти все числа Мерсена меньшие n.. (Простое число называется числом Мерсена, если оно может быть представлено в виде 2ª-1, где a – тоже простое число. Например, 31 =2**³-1 - число Мерсена). 29.2 Дано натуральное число n. Выяснить, является ли оно полным квадратом. Определить функцию, позволяющую распознавать полные квадраты.
	30.1 Дан массив A[1..50], элементы которого отличны от нуля. Расположить их в таком порядке, чтобы первыми были все положительные элементы, а затем - все отрицательные, причем порядок следования как положительных, так и отрицательных элементов должен сохраниться (при решении задачи новый массив не заводить!). 30.2 Составить функцию для нахождения точного значения суммы натуральных чисел, в десятичной записи которых более 20 знаков. Указание. Исходные данные и ответ представить в виде массивов цифр