| Вар. | M [ X ] | D [ X ] | 
| b |
| -2 | ||||
| -1 | ||||
| -1 | ||||
| -8 | -9 | |||
| -2 | ||||
| -1 | ||||
Задание 7.6.
В партии из n изделий каждое может оказаться стандартным с вероятностью p. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет: а) равно m; б) заключено между m1 и m2.
| Вар. | p | n | m | m1 | m2 |
| 0.3 | |||||
| 0,7 | |||||
| 0,5 | |||||
| 0,4 | |||||
| 0,6 | |||||
| 0,2 | |||||
| 0,4 | |||||
| 0,6 | |||||
| 0,3 | |||||
| 0,8 | |||||
| 0,3 | |||||
| 0,7 | |||||
| 0,2 | |||||
| 0,1 | |||||
| 0,5 | |||||
| 0,4 | |||||
| 0,6 | |||||
| 0,2 | |||||
| 0,3 | |||||
| 0,1 | |||||
| 0,7 | |||||
| 0,5 | |||||
| 0,6 | |||||
| 0,8 | |||||
| 0,1 | |||||
| 0,3 | |||||
| 0,2 | |||||
| 0,4 | |||||
| 0,6 | |||||
| 0,5 |
Задание 7.7.
Двумерная случайная величина (X,Y) имеет плотность распределения
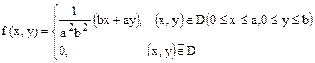
Найти вероятность попадания значения (X,Y) в область 
 вероятность попадания значения X в интервал
вероятность попадания значения X в интервал  математическое ожидание M [ X ] и условное математическое ожидание
математическое ожидание M [ X ] и условное математическое ожидание 
| Вар | a | b | x1 | x2 | y1 | y2 |
| -2 | ||||||
| -4 | ||||||
| -4 | ||||||
| -2 | ||||||
| -1 | ||||||
| -3 | ||||||
| -2 | ||||||
| -1 | ||||||
| -2 | ||||||
| -4 | ||||||
| -3 | ||||||
| -2 | ||||||
| -4 | ||||||
| -4 | ||||||
| -2 | ||||||
| -1 | ||||||
| -3 | ||||||
| -2 | ||||||
| -1 | ||||||
| -2 | ||||||
| -4 | ||||||
| -3 |
Задание 7.8.
Случайная величина Х имеет плотность распределения f (x). Для случайной величины Y = j (X) найти плотность распределения g (y), вероятность P (a £ Y £ b), математическое ожидание M [ Y ] и дисперсию D [ Y ].
1. 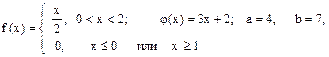
2. 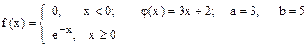
3. 
4. 
5. 
6. 
7. 
8. 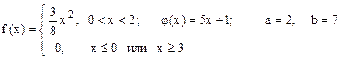
9. 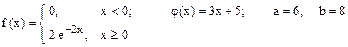
10. 
11. 
12. 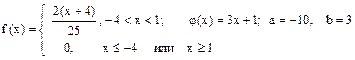
13. 
14. 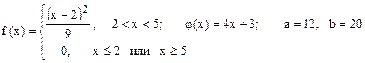
15. 
16. 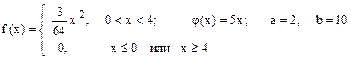
17. 
18. 
19. 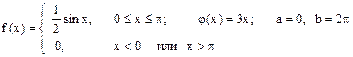
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 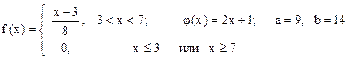
29. 
30. 
Задание 7.9.
Задана матрица перехода системы из состояния i (i =1,2) в состояние j (j =1,2) за один шаг  . Найти матрицу перехода из состояния i в состояние j за два шага.
. Найти матрицу перехода из состояния i в состояние j за два шага.
| Вар. | a | b | C | D |
| 0,1 | 0,9 | 0,2 | 0,8 | |
| 0,2 | 0,8 | 0,7 | 0,3 | |
| 0,3 | 0,7 | 0,4 | 0,6 | |
| 0,4 | 0,6 | 0,5 | 0,5 | |
| 0,6 | 0,4 | 0,7 | 0,3 | |
| 0,6 | 0,4 | 0,8 | 0,2 | |
| 0,8 | 0,2 | 0,9 | 0,1 | |
| 0,8 | 0,2 | 0,2 | 0,8 | |
| 0,9 | 0,1 | 0,2 | 0,8 | |
| 0,4 | 0,6 | 0,1 | 0,9 | |
| 0,7 | 0,3 | 0,2 | 0,8 | |
| 0,5 | 0,5 | 0,4 | 0,6 | |
| 0,3 | 0,7 | 0,2 | 0,8 | |
| 0,2 | 0,8 | 0,5 | 0,5 | |
| 0,9 | 0,1 | 0,7 | 0,3 | |
| 0,9 | 0,1 | 0,8 | 0,2 | |
| 0,8 | 0,2 | 0,3 | 0,7 | |
| 0,4 | 0,6 | 0,3 | 0,7 | |
| 0,5 | 0,5 | 0,4 | 0,6 | |
| 0,3 | 0,7 | 0,6 | 0,4 | |
| 0,8 | 0,2 | 0,4 | 0,6 | |
| 0,2 | 0,8 | 0,5 | 0,5 | |
| 0,2 | 0,8 | 0,1 | 0,9 | |
| 0,4 | 0,6 | 0,7 | 0,3 | |
| 0,1 | 0,9 | 0,4 | 0,6 | |
| 0,2 | 0,8 | 0,7 | 0,3 | |
| 0,4 | 0,6 | 0,5 | 0,5 | |
| 0,2 | 0,8 | 0,2 | 0,8 | |
| 0,5 | 0,5 | 0,3 | 0,7 | |
| 0,7 | 0,3 | 0,9 | 0,1 |
Контрольная работа №8
"Математическая статистика"
Задание 8.1.
Из генеральной совокупности извлечена выборка, представленная в виде статистического ряда (в первой строке указаны выборочные значения, во второй - соответствующие им частоты). Требуется вычислить выборочное среднее, выборочную дисперсию DB, исправленную выборочную дисперсию s2 и среднеквадратическое отклонение s, эмпирическую функцию распределения.
1.
| xi | |||||||
| ni |
2.
| xi | |||||||
| ni |
3.
| xi | |||||||
| ni |
4.
| xi | |||||||
| ni |
5.
| xi | |||||||
| ni |
6.
| xi | |||||||
| ni |
7.
| xi | |||||||
| ni |
8.
| xi | |||||||
| ni |
9.
| xi | |||||||
| ni |
10.
| xi | |||||||
| ni |
11.
| xi | |||||||
| ni |
12.
| xi | 8,5 | 9,5 | 10,5 | 11,5 | 12,5 | 13,5 | 14,5 |
| ni |
13.
| xi | -5 | -3 | -1 | ||||
| ni |
14.
| xi | |||||||
| ni |
15.
| xi | |||||||
| ni |
16.
| xi | |||||||
| ni |
17.
| xi | |||||||
| ni |
18.
| xi | |||||||
| ni |
19.
| xi | |||||||
| ni |
20.
| xi | |||||||
| ni |
21.
| xi | -6 | -4 | -2 | ||||
| ni |
22.
| xi | |||||||
| ni |
23.
| xi | |||||||
| ni |
24.
| xi | |||||||
| ni |
25.
| xi | -2 | ||||||
| ni |
26.
| xi | |||||||
| ni |
27.
| xi | |||||||
| ni |
28.
| xi | |||||||
| ni |
29.
| xi | |||||||
| ni |
30.
| xi | -7 | -5 | -1 | ||||
| ni |
Задание 8.2.
По заданным выборочным среднему и исправленному среднеквадратическому отклонению s найти с доверительной вероятностью p доверительный интервал для математического ожидания M[X], если
а)  известно (принять
известно (принять 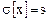 ),
),
б)  неизвестно,
неизвестно,
А также доверительный интервал для. Число степеней свободы принять равным 3.
| Вар. | 
| s | N | p |
| 15,2 | 6,8 | 0,95 | ||
| 20,6 | 8,4 | 0,99 | ||
| 50,8 | 16,3 | 0,95 | ||
| 18,7 | 5,4 | 0,99 | ||
| 27,4 | 8,7 | 0,95 | ||
| 7,2 | 2,8 | 0,95 | ||
| 11,8 | 2,9 | 0,95 | ||
| 15,4 | 3,9 | 0,95 | ||
| 17,3 | 4,6 | 0,95 | ||
| 19,2 | 5,2 | 0,99 | ||
| 21,5 | 6,3 | 0,95 | ||
| 29,3 | 8,9 | 0,99 | ||
| 75,2 | 6,3 | 0,95 | ||
| 76,4 | 10,4 | 0,95 | ||
| 78,7 | 12,2 | 0,99 | ||
| 67,5 | 8,6 | 0,95 | ||
| 63,2 | 7,1 | 0,95 | ||
| 60,8 | 7,3 | 0,99 | ||
| 57,4 | 6,5 | 0,95 | ||
| 48,3 | 7,2 | 0,95 | ||
| 64,1 | 8,3 | 0,95 | ||
| 69,5 | 9,6 | 0,99 | ||
| 73,2 | 10,8 | 0,95 | ||
| 78,1 | 11,2 | 0,99 | ||
| 82,4 | 9,4 | 0,95 | ||
| 15,9 | 10,7 | 0,95 | ||
| 25,3 | 12,8 | 0,99 | ||
| 67,2 | 8,9 | 0,95 | ||
| 71,3 | 11,4 | 0,95 | ||
| 21,9 | 6,4 | 0,99 |
Задание 8.3.
1. Выборку значений CB X, указанную в условии задачи 8.1 сгруппировать, разбивая отрезок [а,b] (a=min xi, b=max xi ) на 5 интервалов одинаковой длины [  ] c границами
] c границами 
и подсчитать частоты nj интервалов.
2. Предполагая, что X распределена по нормальному закону и принимая в качестве оценок его параметров М[X],  [X] выборочное среднее
[X] выборочное среднее  и выборочное среднеквадратическое отклонение s вычислить теоретическое частоты интервалов.
и выборочное среднеквадратическое отклонение s вычислить теоретическое частоты интервалов.
3. С помощью критерия согласия Пирсона при уровне значимости  =0,1 проверить, согласуются ли выборочные данные с гипотезой о нормальном распределении величины Х. Число степеней свободы принять равным 3.
=0,1 проверить, согласуются ли выборочные данные с гипотезой о нормальном распределении величины Х. Число степеней свободы принять равным 3.
Задание 8.4.
По заданной корреляционной таблице найти выборочные средние среднеквадратические отклонения sx, sy, коэффициент корреляции и уравнение линейной регрессии Y на X. Вычислить условные средние по данным таблицы и с помощью выборочного уравнения регрессии и найти наибольшее их отклонение.
1.
| У Х | nх | |||||
| ny |
2.
| Y X | Nx | |||||
| ny |
3.
| Y X | nx | ||||||
| ny |
4.
| Y X | nx | |||||
| ny |
5.
 Y
X Y
X
| N x | ||||||
| ny |
6.
| Y X | nx | ||||||
| ny |
7.
| Y X | N x | ||||||
| ny |
8.
| Y X | nx | ||||||
| ny |
9.
| Y X | Nx | ||||||
| ny |
10.
| Y X | nx | |||||
| ny |
| Y X | Nx | |||||
| ny |
12.
| Y X | nx | |||||
| ny |
13.
| Y X | nx | |||||
| ny |
14.
| Y X | nx | |||||
| ny |
15.
| Y X | nx | |||||
| ny |
16.
| Y X | nx | ||||||
| ny |
17.
| Y X | nx | ||||||
| ny |
18.
| Y X | nx | ||||||
| ny |
19.
| Y X | nx | ||||||
| ny |
20.
| Y X | nx | |||||
| ny |
21.
| Y X | nx | ||||||
| ny |
22.
| Y X | nx | ||||||
| ny |
23.
| Y X | nx | |||||||||||
Дата добавления: 2016-11-18; Мы поможем в написании ваших работ!; просмотров: 777 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.016 с.






