Основное условие проведения выборочного наблюдения - предупреждение систематических ошибок, возникающих при нарушении принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Выборка может быть:
1) собственно случайная;
2) механическая
3) типическая
4) серийная
5) комбинированная
1. Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного отбора единиц из генеральной совокупности. Это достигается путем присвоения каждой единицы генеральной совокупности порядкового номера, который затем записывается на фишки или шары одинакового размера и формы. Фишки или шары тщательно перемешиваются и отбираются по одной. Можно также использовать таблицы случайных чисел.
Для вычисления средней ошибки выборки используются формулы:
При повторном отборе 
; при бесповторном отборе 
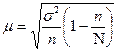
2. При механическом отборе генеральная совокупность разбивается на группы (равные интервалы). При этом величина интервала равна обратной величине доли выборки и из каждой группы отбирается только одна единица (так при 2% выборки отбирается каждая 50-я единица, при 5%, каждая 20-я единица). Чаще всего для избежания систематических ошибок отбираются те единицы, которые находятся в середине группы. Для определения средней ошибки механической выборки используется та же формула, что и при собственно-случайном отборе.
3. При типической выборке генеральная совокупность разбивается на однородные типические группы, а затем из каждой типической группы собственно-случайной или механической выборкой производится отбор единиц в выборочную совокупность. Типическая выборка применяется обычно при изучении сложных статистических совокупностей. Она дает более точные результаты по сравнению с другими способами отбора.
При определении ошибки типической выборки находят среднюю из внутригрупповых дисперсий:
а) для доли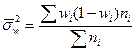 
;
б)для средней 
Тогда для определения средней ошибки выборки используются формулы:
а) для доли альтернативного признака при повторном отборе: 
для бесповторного отбора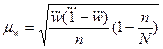 
б) для средней величины для повторного отбора 
;
для бесповторного отбора 
4. При серийной выборки из генеральной совокупности отбираются не отдельные единицы, а целые их гнезда (группы). Внутри каждой серии обследуются все без исключения единицы (применяется сплошное наблюдение). Применяется серийные выборки, например, в торговле, где целесообразнее проверить несколько коробок, чем вытаскивать из каждой коробки по пачке. Серийная выборка производится по схеме бесповторного отбора. Для определения средней ошибки выборки применяются формулы:
а) для доли 
, где 
- межсирийная дисперсия выборочной доли,
r – число серий в выборке;
R – число серий в генеральной совокупности.
б) для средней 
где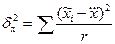 
5. Комбинированную выборку применяют в случае, когда отбор единиц из генеральной совокупности представляет собой сложный процесс. Можно, например, комбинировать серийный отбор со случайной выборкой. Пи этом генеральная совокупность разбивается сначала на серии, а затем в каждой серии проводится случайный отбор. Средняя ошибка комбинированной выборки определяется по формулам: при повторном отборе 
при бесповторном отборе 
,
где n – число единиц, взятых в выборку из серий.
Различат одноступенчатые и многоступенчатые способы отбора единиц в выборочную совокупность. При одноступенчатой выборке каждая единица сразу же подвергается изучению по заданному признаку. При многоступенчатой выборке производится отбор из генеральной совокупности отдельных групп, а из групп отбираются отдельные единицы.
Средняя ошибка выборки при многоступенчатом отборе равна
,
где 
- средние ошибки выборки на отдельных ступенях отбора, n1,n2,…,nn- численность выборки на соответствующих ступенях отбора.
