Задание из курса

Задание 1. Построение положения и величины ребер

многогранника за их координатами.

 

Условие.

построить проекцию призмы;

из точки Е построить перпендикуляр к прямой уровня АВ и найти следы данного перпендикуляра;

ребро ВЕ разделить точкой К в заданном отношении;

определить натуральную величину відрізка АС и угол наклона к плоскости проекции.

Координата точки задана по вариантам и приведена в таблице 1.

Ход выполнения задания:

1) за координатой строят проекцию точки А, С,Е

2) из точки А вправо вниз провести черту уровня по заданному углу и довжіні (а – горизонталь, бы – фронталь) в результате чего получим точку В;

3) соединив точку В с точкой Е получим ребро ВЕ призмы АВСfed (ребра AD и CF уровни за величиной и параллельные ВЕ) и таким образом построим призму;

4) из точки Е строим перпендикуляр к прямой АВ;

5) строим горизонтальный, фронтальный и профильный следы перпендикуляра (студенты заочного отделения строят два проекции призмы и соответственно находят только горизонтальный и фронтальный следы);

6) делимо ребро ВЕ точкой К в заданном отношении;

7) определяем методом прямоугольного треугольника натуральную величину ребра АС и угол его наклона к заданной плоскости проекции (? - угол наклона к горизонтальной плоскости проекции? - угол наклона к фронтальной плоскости проекции).

 

Необходимы теоретические сведения.

Если прямая в пространстве параллельна горизонтальной плоскости проекции (горизон­тальна прямая), тогда фронтальная проекция прямой (рис. 1.1 а) параллельна вехе проек­цій, а горизонтальная проекция ав является действительной величиной відрізка и образует с осью проекции действительную величину угла наклона прямой к фронтальной плоскости проекции (угол?).

Прямая фронтальные и профильные владеют теми же свойствами, что и горизон­тальні, но в соответствии с фронтальной (рис. 1.1 бы) и профильной (рис. 1.1 в) плоскостью проекции.

 

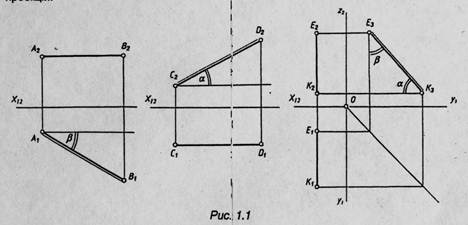
Если прямая в пространстве перпендикулярна горизонтальной плоскости проекции (го­ризонтально проекціювальна), тогда горизонтальная проекция прямой (рис. 1.2 а) точка, а фронтальная проекция прямой перпендикулярна к вехе проекции и есть действительной величи­ною відрізка. Фронтально проекціювальна и профильно проекціювальна прямая и влас-

тивості их проекции приведено соответственно на рис. 1.2 6, в. Прямая, не параллельная и не перпендикулярная плоскости проекции, - прямая общего положения. В этом випад­ку всю проекцию такой прямой имеют непрямые углы с осью проекции (рис. 1.3).

Только после такой проверки свойств проекции прямой запись переносит на лист. На проекции показывают подвій­ними линией и двойной дугой натуральную величину ребер и углов наклона ребер к плоскости проекции.

Для определения натуральной величины ребер общего положения и углов на­хилу его к плоскости проекции нужно применить способ прямоугольного треугольника. На рис. 1.4 рассмотрен способ прямоугольного треугольника, который заключается в том, что строится прямоугольный треугольник авв1, один катет ав которого есть проекция ребра, второй катет вв1 является разницей координаты другой проекции этого ребра, тогда гипотенуза ав1 - нату­ральна величина этого ребра, а угол между проекцией ав, и гипотенузой ав1, равняется углу наклона ребра к соответствующей плоскости проекции.

Чтобы определить углы наклона ребра к горизонтальной, фронтальной и профильной плоскости проекции, строят прямоугольные треугольники на всей проекции. На рис. 1.5 выполненное построение натуральной величины прямой АВ и углов но и? наклону ее к плоскости проекции. Построение понятно из рисунка.

Вслед прямой есть точка пересечения пря­мої с плоскостью проекции, и эта точка (след) одновременно принадлежит прямой и плоскости прое­кцій (рис. 1.6 а) точки Н, F. Так как следует на­лежить плоскости

 

Рис. 1.6

проекции, потому одна проек­ція следу (Н2|) есть точка пересечения проекции прямой с осью Х12, а другая проекция следа Нь Н2 строится как точка, которая принадлежит этой прямой. На рис. 1.6 бы приведен пример по­будови проекции следа Н и F для прямой АВ, на рис. 1.7 у прямой CD.

 

 

Рис. 1.7

Образец выполнения задания.

 

Таблица 1

Варианты заданий к теме: «Точка и прямая»

 

Вариант 1

Вариант 2

Вариант 3

Вариант 4

А

А

А

А

С

С

С

С

Е

Е

Е

Е

а)? = 30° 1 = 25 мм 3) ВК:КЕ=2:3 4)?

б)?= 60?, 1= 30мм 3) ВК:КЕ=3:2 4)?

б)? = 45° 1 = 30 мм 3)ВК:КЕ=1:3 4)?

а)? = 45° 1 = 50 мм 3) ВК:КЕ=2:1 4)?

Вариант 5

Вариант 6

Вариант 7

Вариант 8

А

А

А

А

С

С

С

С

Е

Е

Е

Е

б)?= 45°, 1 = 35 мм 3) ВК:КЕ=2:1 4)?

б)? = 45° 1 = 30 мм 3) ВК:КЕ=2:4 4)?

а)?= 45° 1 = 50 мм 3)ВК:КЕ=2:3 4)?

б)?= 60° 1 = 30 мм 3) ВК:КЕ=2:3 4)?

Вариант 9

Вариант 10

Вариант 11

Вариант 12

А

А

А

А

С

С

С

С

Е

Е

Е

Е

б)? = 30° 1 = 30 мм, 3)ВК:КЕ=1:3 4)?

а)? = 60° ,1 = 20 мм 3)ВК:КЕ=3:1 4)?

б)? = 45° 1 = 30 мм 3)ВК:КЕ=1:2 4)?

б)? = 30° 1 = 30 мм 3) ВК:КЕ=4:2 4)?

Вариант 13

Вариант 14

Вариант 15

Вариант 16

А

А

А

А

С

С

С

С

Е

Е

Е

Е

а)? = 60? 1 = 30 мм 3) ВК:КЕ=3:2 4)?

б)?= 45?, 1 = 30 мм 3) ВК:КЕ=4:3 4)?

б)? = 30° 1 = 30 мм 3) ВК:КЕ=3:2 4)?

а)? = 60° 1 = 60 мм 3) ВК:КЕ=3:1 4)?

 

Продолжение таблицы 1

 

Вариант 17

Вариант 18

Вариант 19

Вариант 20

А

А

А

А

С

С

С

С

Е

Е

Е

Е

б) а = 30° 1 = 20 мм 3) ВК:КЕ=4:2 4)?

б) а = 45 1 = 30мм 3) ВК:КЕ=2:4 4)?

а)? = 60° 1 = 60 мм 3) ВК:КЕ=3:1 4)?

б)? = 30° 1 = 20 мм 3) ВК:КЕ=4:1 4)?

Вариант 21

Вариант 22

Вариант 23

Вариант 24

А

А

А

А

С

С

С

С

Е

Е

Е

Е

а)? = 60°,1 = 30 мм 3) ВК:КЕ=4:3 4)?

б)? = 60 1 = 30 мм 3) ВК:КЕ=3:2 4)?

а)? = 60 1 = 20 мм 3)ВК:КЕ=2:1 4)?

б)? = 60° 1 = 30 мм 3) ВК:КЕ=3:2 4)?

Вариант 25

Вариант 26

Вариант 27

Вариант 28

А

А

А

А

С

С

С

С

Е

Е

Е

Е

а)? = 60,1 = 40 мм 3) ВК:КЕ=2:1 4)?

б) а = 30°, 1 = 30 мм 3)ВК:КЕ=3:1 4)?

а)? =30°,1 = 30 мм 3)ВК:КЕ=3:1 4)?

бы)? = 60°,1 = 60мм 3)ВК:КЕ=1:4 4)?

Вариант 29

Вариант 30

Вариант 31

Вариант 32

А

А

А

А

С

С

С

С

Е

Е

Е

Е

а)? = 45°, 1 = 30 мм 3)ВК:КЕ=1:2 4)?

б)? = 45°, 1 = 20 мм 3) ВК:КЕ=2:4 4)?

а)? = 30°, 1 = 25 мм 3) ВК:КЕ=2:3 4)?

б)? = 60 1 = 30 мм 3) ВК:КЕ=3:2 4)?

 

 

Вопрос для самоконтроля:

1.Как изображается в проекции прямая особенного и общего положения?

2.Какая прямая изображается в натуральную величину на проекции?

3.В каком разе угол наклона прямой к плоскости проекции изображается в натуральную величину?

4.В чем суть способа прямоугольного треугольника?

5.Почему одна из проекции фронтального, горизонтального следов лежат на осе проекции?

 

 

Задание 2. Плоскость. Взаимно перпендикулярная и параллельная плоскость

Условие:

а) определить натуральную величину расстояния от точки D к плоскости за­даної треугольником АВС

б) построить плоскость, параллельную плоскости трикутни­ка ABC, которая удалена от ее на 35 мм;

в) через вершину У треугольника АВС построить плоскость перпендикулярную заданному треугольнику, найти линию их взаимного пересечения, и показать видимость и невидимость элементов плоскости.

Координата точки по варі­антах приведена в таблице 2.

Теоретические ввідомості

Расстояние от точки к плоскости измеряется перпендикуляром, опущенным из точ­ки на эту плоскость. Следовательно, в этой задаче нужно из точки D провести перпендикулярную прямую к плоскости АВС, построить точку пересечения этой перпендикулярной прямой с плоскостью АВС и способом прямоугольного треугольника определить натуральную величину перпендикуляра.

Для построения перпендикуляра к плоскости нужно использовать свойство пря­мого угла. Прямой угол между прямой проекціюється в натуральную величину(90°) на соответствующую плоскость проекции, если хотя бы одна из его стороны параллельная к этой плоскости проекции (см. рис. 1.8).

 

Рис. 1.8

 

 

Использовав горизонталь и фронталь как прямую, параллельную к соответствующей плоскости проекции, построим проекции (nm и n'm') (рис. 1.9) прямой NM, перпендикулярной к плоскости АВС.

 

 

.Рис. 1.9

 

Для построения точки пересечения прямой с плоскостью необходимо скори­статися свойствами проекціювальних плоскости. На рис. 1.10 через прямую n прове­дена фронтальная проекціювальна плоскость?. Построена линия пересечения плоскости АВС и? (1 2 = АВС x?). Линия 12 одновременно принадлежат обоим плоскости и, соответственно, будет линией их пересечения. Пересечение проекции линии 1 2 из n определит горизонтальную проекцию N, точка пересечения прямой л с плоскостью АВС. Фронтальная проекция n' строится за принадлежностью точки N прямой n.

Видимость прямой n на проекции определяют с помощью конкурирующей точки (1, 3 и 4, 5). Построение понятно из рисунка.

Натуральную величину расстояния от точки D к плоскости АВС (отрезок DK) ви­значають способом прямоугольного треугольника (см. рис. 1.5). На рис. 1.11 приведен пример выполнения задания 2. Для построения плоскости, отдаленной на 35 мм от заданной в произвольной точке плоскости треугольника АВС, например, в вершине А, строят перпенди­куляр к плоскости. На проекции перпендику­ляра берут произвольную точку Е и способом прямоугольного треугольника определяют нату­ральну величину відрізка ЕА. Отложив на отрезке ЕА (гипотенузе) нужную длину (35 мм), строят подобные треугольники и получают проекцию точки М, которая отдалена на 35 мм от заданной плоскости.

Через точку М надлежат построить пло­щину параллельную плоскости треугольника АВС. Два плоскости параллельные, если две прямая, которая пересекается, одной плоскости, соответственно параллельные двум прямой, которая пересекается, второй плоскости. Исходя из условий паралель­ності двух плоскости, плоскость определяют дво­ма прямой но и в, которые проходят через точку М за условия что а АВ, а в АС.

Построение плоскости перпендикулярной к заданной выполняют опираясь на свойства перпендикулярности двух плоскости. Плоскость перпендикулярна ко второй плоскости, если она проходить через перпенди­куляр к ей. Решение этой задачи сводится к построению перпендикуляра к заданной плоскости.

В приведенном примере через точку У треугольника АВС строят фронталь и горизонталь, пер­пендикулярні к прямой АС (см. рис. 1.11). Построена фронталь f и горизонталь h определят плоскость, перпендикулярную к плоскости АВС. Чтобы определить линию вза­ємного пересечения определенной плоскости, необходимо найти точку пересечения прямой АС или FH одной плоскости со второй плоскостью.

 

Образец выполнения задания

 

 

Таблица 2

 

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

Вариант 1

Вариант 2

Вариант 3

Вариант 4

A

B

C

D

Вариант 5

Вариант 6

Вариант 7

Вариант 8

A

B

C

D

Вариант 9

Вариант 10

Вариант 11

Вариант 12

A

B

C

D

Вариант 13

Вариант 14

Вариант 15

Вариант 16

A

B

C

D

Вариант 17

Вариант 18

Вариант 19

Вариант 20

A

B

C

D

Вариант 21

Вариант 22

Вариант 23

Вариант 24

A

B

C

D

Вариант 25

Вариант 26

Вариант 27

Вариант 28

A

B

C

D

Вариант 29

Вариант 30

Вариант 31

Вариант 32

A

B

C

D

 

Вопрос для самоконтроля:

1. Как задать плоскость перпендикулярную к прямой?

2. Как построить проекцию угла наклона прямой общего положения к плоскости общего положения?

3. Как построить проекцию перпендикуляра к заданной плоскости через зада­ну точку?

4. Как построить проекцию линии пересечения двух плоскости?

5. Какие способы превращения проекции можно использовать для построения лі­нії пересечения двух плоскости?

6. С помощью каких способов превращения можно найти натуральную ве­личину плоской фигуры?

 

 

Задание 3. Исследование многогранника с применением способов превращения проекции

Условие. В заданном многограннике определить:

а) расстояние между отмеченными па­ралельними ребрами;

б) кратчайшее расстояние между отмеченными мимолетными ребра­ми;

в) расстояние от вершины к ребру или грани;

г) расстояние от ребра к параллельной ему грани;

д) расстояние между параллельной гранью;

є) величину угла между двумя гра­нями при отмеченном ребре.

Варианты задания приведены в таблице 3.

Теоретические сведения

Для выполнения данного задания необходимо владеть метрическими свойствами проекции пары геометрической фигуры. Рассмотрим некоторые свойства в соответствии с заданием.

• Расстояние между двумя параллельной прямой проекціюється в натуральную вели­чину на одну из плоскости проекции, если они будут проекціювальними к пло­щини проекции (рис. 1.15 а).

• Расстояние между двумя мимолетной прямой проекціюється в натуральную величи­ну, если их плоскость параллелизма есть проекціювальними (рис. 1.15 бы).

• Расстояние от точки к прямой проекціюється в натуральную величину, если прямая занимает проекціювальне положение (рис. 1.15 в).

• Расстояние от точки к плоскости проекціюється в натуральную величину, если пло­щина будет проекціювальна (рис. 1.15г/

• Расстояние от прямой к параллельной ей плоскости проекціюється в натуральную ве­личину, если плоскость занимает проекціювальне положение (рис. 1.15 д).

• Расстояние между двумя параллельной плоскостью проекціюється в натуральную ве­личину, если эта плоскость будет проекціювальними (рис. 1.15 есть).

• Угол между двумя плоскостью (гранью) проекціюється в натуральную величину, як­що его плоскости (грань) проекціювальні к плоскости проекции (рис. 1.15 же).

Исходя из условия задания и свойств пары геометрической фигуры необходимо способами превращения проекции привести заданную геометрическую фигуру в проекціюва­льне положение. Способы превращения проекции используют для изменения поло­ження определенного объекта относительно плоскости проекции, например, для приведения геоме­тричних элементов (прямой и плоскости) общего положения в особенные положения (проекціювальні или параллельные к плоскости проекции).

В способе плоскопараллельного перемещения допускают неизменными площи­ни проекцию, а в способе замены плоскости проекции - неизменным остается объект.

Способ плоскопараллельного перемещения является способом вращения вокруг невия-влених оси, перпендикулярной к плоскости проекции. Плоскопараллельное переміщен­ня - перемещение при котором вся точка геометрической фигуры (объекта) переміща­ються во взаимно параллельной плоскости относительно плоскости проекции без изменения фор­ми и размеров. При таком перемещении точка хранит свое расстояние к відповід­них плоскости проекции.

 

 

В способе замены плоскости проекции новая плоскость проекции выбирается перпен­дикулярною к одной из тех, что остается, и потому расстояние от точки к плоскости, которая остается, хранит свою величину на новой проекции.

Способом превращения проекции можно разместить:

1. Прямую общего положения параллельно плоскости проекции;

2. Прямую общего положения в проекціювальне положение к плоскости проекции.

3. Плоскость общего положения параллельно плоскости проекции.

4. Плоскость общего положения в проекціювальне положение к плоскости проек­цій.

К названной четырем задаче сводится роз'язання всей метрической задачи. Напри­клад, на основе первой задачи определяют натуральную величину отрезков; на основе второй задачи - натуральную величину расстояния между точкой и прямой, двумя прямой, прямой и плоскостью, двугранный угол; с помощью третьей задачи определяют нату­ральні величину плоской фигуры, углы мимобіжності и пересечению; на основе четвертой за­дачі определяют расстояния между прямой и плоскостью и между двумя плоскостью.

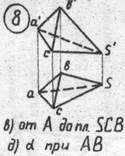
В приведенном примере на рис. 1.16 способом замены плоскости проекции визначе­на расстояние между вершиной В ребром АЅ. Для этого двойной заменой плоскости проекции ребро АЅ превращено в проекціювальне положение. Сначала виб­рано ось проекции х14 параллельно ребру АЅ. На построенной проекции ребро розміс­тилось параллельно /74, спроекціювалось в натуральную величину. Вторую ось х45 виб­рано перпендикулярно к А4Ѕ4. На новой плоскости проекции ребро АЅ спроекціюється в точку АЅ(проекціювальне). Расстояние от А5 Ѕ5 к проекции В5 есть искомая від­стань между прямимою АЅ и вершиной В.

На примере также способом плоско параллельного перемещения определена натураль­на величина угла между гранью при ребре АВ. Ребро АВ, как общее ребро для гра­ней АВs и АВС двумя перемещениями приведено в проекціювальне положение и соответственно грани АВs и АВС - проекціювальні.

Угол а между проекцией плоскости - искомый угол?.

 

Образец выполнения задания.

 

Таблица 3

Варианты заданий к теме «Исследования многогранника»

 

			АВ и Еf
	? при ЭД

 

 

 

Вопрос для самоконтроля:

1. В чем суть способов плоско параллельного перемещения и замены плоскости проек­цій?

2. Как определить ось вращения при использовании способа плоско параллельного перемещения?

3. Как превратить плоскость общего положения в проекціювальне положение?

4. Каким превращением можно разместить прямую или плоскость параллельно площи­ні проекции?

5. Можно ли прямую общего положения заменой одной плоскости проекции розмі­стити в проекціювальне положение?

 

Задание 4. Перерез многогранника плоскостью и построение натуральной величины перерезу

Условие. Построить перерез данного многогранника плоскостью общего поло­ження. Определить натуральную величину фигуры перерезу. Построить развертку фигуры и нанести линию перерезу на развертку.

Теоретические сведения.

Основой для выполнения этого задания является задача на пересечение прямой из площи­ною. Эту задачу можно развязать, использовав вспомогательную секущую плоскость (см. рис. 1.10). При использовании способа вспомогательной секущей плоскости проекціювальні январе плоскость предлагается проводить через ребра многогранника. Задача сводится к определению точки встречи прямой с проекціювальною плоскостью.

Для упрощения решения задачи целесообразнее использовать один из способов перетво­рення проекции: косоугольное вспомогательное проекціювання; замену плоскости проекции.

При косокутньому вспомогательном проекціюванні на горизонтальную или фронтальную плоскость проекции или на вертикальную, проекціювання выполняют в направлении прямой, которая принадлежит секущей плоскости общего положения. При этом плоскость спроекцію­ється в прямую линию (след плоскость), а многогранник - в новую вспомогательную проекцию.

Пересечение вспомогательной проекции ребер многогранника со следом плоскости перерезу (проекціювальне положение плоскости) определит вершину многоугольника перерезу. Обратном проекціювання строят их фронтальная и горизонтальная проекция.

Пересечение наклонной треугольной пирамиды плоскостью общего положения зображе­но на рис. 1.19. Здесь использован косоугольное вспомогательное проекціювання на плоскость проекции П1 в направлении фронталі плоскости. При таком проекціюванні плоскость спроек­ціюється своим горизонтальным следом /?,, а ребра пирамиды - пучком прямой. Центр пучка достанем, если вершину пирамиды 5 спроекціюємо в направлении фронталі на пло­щині П1 в точку 5. Сполучивши центр пу­чка 51 с точкой основы пирамиды, отрима­ємо вспомогательную проекцию пирамиды. В пере­тині вспомогательной проекции ребер из проекці­єю плоскости /т, будем иметь три вспомогательной проекции: ее, 2і, Из точки пересечения ребер пирамиды с секущей пощиною

 

Обратным проекціюванням в направлении фронталі находим точку 1-, 2Ь 31, а затем - фронтальная проекция 12, 22, 32 этой точки. Соединяя их, получим трикут­ник перерезу.

При замене плоскости проекции задача сводится к построению новой проекции, где плоскость перерезу должна занимать проекціювальне положение, а до­поміжна проекция многогранника занимает соответствующее положение при данном способе превращения проекции.

Способ построения перерезу многогранника плоскостью студент выбирает самостійнотак, а построение натуральной величины перерезу желательно выполнить методом вращение вокруг линии уровня. Задание по вавріантам студент выбирает из таблицы.

 

Образец выполнения задания

 

Вопрос для самоконтроля:

1. Какая позиционная задача положена в основу построения плоского перерезу многогранника?

2. В каких случаях целесообразнее применять способ вспомогательного проекціювання, а в которых - способ вспомогательной секущей плоскости?

3. Какими способами можно определить натуральную величину перереза?