Я сменю у каждого слагаемого знак, делать это не обязательно, просто запись будет выглядеть стандартнее что ли:
Дальше алгоритм работает по накатанной колее, важно только уметь решать неоднородное уравнение 1-го порядка:
Проведем замену: 
Составим и решим систему:
Из первого уравнения найдем 
:
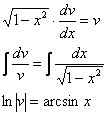
– подставим найденную функцию во второе уравнение системы:
Подобные интегралы я ласково называю дурными интегралами, они не столько сложные, сколько творческие – нужно догадаться (хотя бы научным тыком), как их решать.
Данный интеграл берётся по частям:
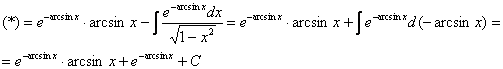
Творчество присутствует, помимо интегрирования по частям, использован метод подведения функции под знак дифференциала.
Таким образом:
Но это ещё не всё, выполняем обратную замену:
Если изначально было 
, то обратно будет 
В результате получаем общее решение исходного уравнения Бернулли:
Решим задачу Коши. Найдем частное решение, удовлетворяющее начальному условию 
:
Ответ: частное решение: 
Для монстров дифференциального исчисления вкратце напоминаю алгоритм проверки дифференциального уравнения:
1) Проверяем, выполнено ли начальное условие.
2) Берём ответ 
и находим производную 
.
3) Подставляем ответ и найденную производную в исходное ДУ. Должно получиться верное равенство.
Проверить дифференциальное уравнение Бернулли действительно не всем под силу, так как в большинстве случаев приходится находить трудную производную и выполнять громоздкую подстановку.
Когда я подбирал первый пример для этой статьи, очень хотелось разобрать распространенное уравнение Бернулли в духе 
, однако сразу же после замены оно становится до неприличия похоже на Пример 8 урока неоднородные дифференциальные уравнения первого порядка. Поэтому пусть лучше будет что-нибудь необычное.
Но, вы не расстраивайтесь, вот пара более простых примеров для самостоятельного решения:
Пример 2
Найти решение ДУ 
, удовлетворяющее начальному условию 
Пример 3
Найти решение задачи Коши
,
Полные решения и ответы в конце урока.
В третьем примере перед решением целесообразно представить уравнение в стандартном виде: 
.
Вообще, иногда составители сборников и методичек зашифровывают уравнения до неузнаваемости, например:
Как говорится, сиди студент и разгадывай ребус – какого хрена типа этот диффур. То ли уравнение с разделяющимися переменными, то ли уравнение в полных дифференциалах, то ли еще какое-нибудь уравнение.
Пример 4
Найти решение ДУ 
, соответствующее начальному условию 
Корни, куда же без них.
Решение: Пожалуйста, классический вид 
уравнения Бернулли.
Сначала убираем «игрек» из правой части, для этого делим каждую часть на 
:
Теперь с помощью замены нужно избавиться от «игрека» вот в этом слагаемом:
Из вышесказанного следует замена: 
Найдем производную:
, откуда выразим: 
Таким образом:
Получено линейное неоднородное уравнение, проведем замену:
Составим и решим систему: 
.
Из первого уравнения найдем :
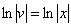
– подставим во второе уравнение:
Таким образом: 
Обратная замена: если , то 
Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:
Ответ: частное решение: 
Кстати, данное уравнение очень легко проверить.
Возможно, некоторые удивились, почему я ничего не рассказал про математика Бернулли. Забыл. Не будем нарушать традиций. Якоб Бернулли почти итальянец, жил в Швейцарии, говорил на 5-ти языках. В семье Бернулли 9 (!) математиков, одним словом – династия. Но с этой фамилией у меня стойко ассоциируются строчки гимна физмата:
Три дня в деканате покойник лежал, в штаны Пифагора одетый,
В руках Фихтенгольца он томик держал, что сжил его с белого света,
К ногам привязали тройной интеграл, и в матрицу труп обернули,
А вместо молитвы какой-то нахал прочёл теорему Бернулли.
Пример 5
Найти общее решение (или общий интеграл) дифференциального уравнения первого порядка.
Немногочисленный пример из моей выборки, когда требуется найти только общее решение. Полное решение и ответ в конце урока.
Мы рассмотрели наиболее распространенные версии уравнения Бернулли – с «игреком» во второй степени и с «игреком» под квадратным корнем. Другие варианты встречаются реже. Разберём пример, когда «игрек» находится в кубе.
Пример 6
Найти общее решение дифференциального уравнения
Решение: Данное ДУ является уравнением Бернулли. Разделим обе части на 
:
Избавляемся от «игрека» в «полюбившемся» слагаемом, для этого проведем замену:
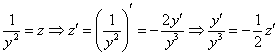
В результате:
Получено линейное уравнение, проведем замену:
Решим систему:
Из первого уравнения найдем :
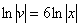
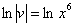
– подставим во второе уравнение:
Таким образом: 
Проведём обратную замену: если изначально 
, то обратно: 
В принципе, здесь можно выразить общее решение в виде:
, но, согласитесь, смотрится не очень…, словно Дедушка Мороз подсунул в подарок гнилую мандаринку. Эта фишка уже рассматривалась мной на уроке Однородные дифференциальные уравнения первого порядка. Нет-нет, испорченные продукты питания никому не предлагал =)
Лично я в похожей ситуации почти всегда склоняюсь к тому, чтобы оставить ответ в виде общего интеграла (заодно париться не нужно).
Ответ: общий интеграл: 
Ещё одно решение: 
Когда вам предложено найти только общее решение уравнения Бернулли, ответ полезно дополнить тривиальным решением .
Перед кремлёвским салютом рассмотрим заключительный пример с отрицательной степенью.
Пример 7
Найти частное решение дифференциального уравнения
, 
Это пример для самостоятельного решения.
Ну вот, мешок с подарками пуст, надеюсь все остались довольны. Хотя, честно, Новый Год не люблю, сегодня вычитал на Анекдоте.ру меткий афоризм: 10 дней праздников обычно проводишь либо без всякой пользы либо с большим вредом.
Удачной вам сессии!
Решения и ответы:
Пример 2: Решение: Данное ДУ является уравнением Бернулли. Найдем общее решение.
Проведем замену: 
Получено линейное неоднородное уравнение, замена: .
Составим и решим систему: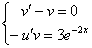 
Из первого уравнения найдем :
– подставим во второе уравнение:
Таким образом: 
Обратная замена:
Общее решение: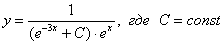 
Найдем частное решение, соответствующее заданному начальному условию:
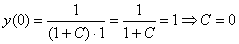
Ответ: частное решение: 
Красиво.
Пример 3: Решение:
Данное дифференциальное уравнение является уравнением Бернулли, разделим обе части на 
:
Проведем замену:
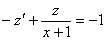
Получено линейное неоднородное уравнение, проведем замену:
Составим и решим систему:
Из первого уравнения найдем :
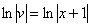
– подставим во второе уравнение:
Таким образом:
Обратная замена:
Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:
Ответ: частное решение: 
Пример 5: Решение: Данное уравнение является уравнением Бернулли
Замена: 
В полученном линейном неоднородном уравнении, проведем замену:
Решим систему: 
.
Из первого уравнения найдем :
– подставим во второе уравнение:
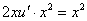
Таким образом:
Общее решение: 
Обратная замена:
Ответ: общее решение 
! Примечание: Не забывайте про тривиальное решение , его бывает не лишним включить в ответ.
Пример 7: Решение: 
Данное ДУ является уравнением Бернулли.
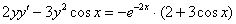
Проведем замену: 
Получено линейное неоднородное уравнение, проведем замену:
Составим и решим систему:
Из первого уравнения найдем :
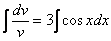
– подставим во второе уравнение:
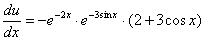
Таким образом:
Обратная замена: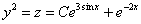 
Частное решение, соответствующее начальному условию , можно найти прямо из общего интеграла 
. Для этого вместо «икса» подставляем ноль, а вместо «игрека» – единицу:
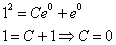
Таким образом, частное решение:
Частное решение также выясняется и более «привычным» способом через общее решение 
.
Ответ: частное решение: 
