Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
1) косвенный метод наименьших квадратов;
2) двухшаговый метод наименьших квадратов;
3) трехшаговый метод наименьших квадратов;
4) метод максимального правдоподобия с полной информацией;
5) метод максимального правдоподобия при ограниченной информации.
Рассмотрим вкратце сущность каждого из этих методов.
Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.
1. Структурная модель преобразовывается в приведенную форму модели.
2. Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты 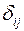 .
.
3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).
Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.
Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной  и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
1) все уравнения системы сверхидентифицируемы;
2) система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Для примера, рассмотренного в предыдущем параграфе, необходимо применить именно двухшаговый метод наименьших квадратов. Но можно сделать следующее замечание. Если из модели исключить тождество дохода, число эндогенных переменных модели снизится на единицу – переменная  станет экзогенной. А число предопределенных переменных модели не изменится, т.к. из модели будет исключена эндогенная переменная
станет экзогенной. А число предопределенных переменных модели не изменится, т.к. из модели будет исключена эндогенная переменная  , но ее место займет переменная
, но ее место займет переменная  . В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной
. В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной  от эндогенной переменной
от эндогенной переменной 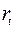 (которая зависит только от предопределенных переменных) и предопределенной переменной
(которая зависит только от предопределенных переменных) и предопределенной переменной 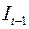 . Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования уравнения на идентификацию.
. Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования уравнения на идентификацию.
Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легко реализуемы.
Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андерсоном и Н.Рубиным.
В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.
Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.






