Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через  .
.
Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через  .
.
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия, социальное положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.
Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты 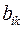 и экзогенных переменных – коэффициенты
и экзогенных переменных – коэффициенты 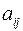 , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под
, которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под  подразумевается
подразумевается 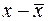 , а под
, а под  – соответственно
– соответственно 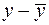 . Поэтому свободный член в каждом уравнении системы (3.3) отсутствует.
. Поэтому свободный член в каждом уравнении системы (3.3) отсутствует.
Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
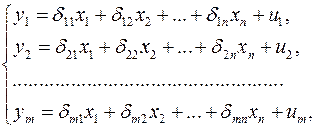 (3.4)
(3.4)
где 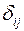 – коэффициенты приведенной формы модели,
– коэффициенты приведенной формы модели, 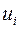 – остаточная величина для приведенной формы.
– остаточная величина для приведенной формы.
По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить 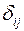 , а затем оценить значения эндогенных переменных через экзогенные.
, а затем оценить значения эндогенных переменных через экзогенные.
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели.
Для структурной модели вида
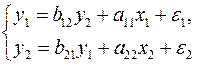 (3.5)
(3.5)
приведенная форма модели имеет вид
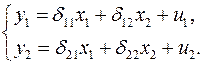 (3.6)
(3.6)
Из первого уравнения (3.5) можно выразить 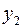 следующим образом (ради упрощения опускаем случайную величину):
следующим образом (ради упрощения опускаем случайную величину):
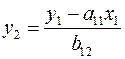 .
.
Подставляя во второе уравнение (3.5), имеем
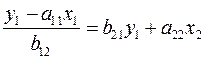 ,
,
откуда
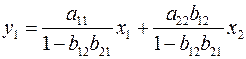 .
.
Поступая аналогично со вторым уравнением системы (3.5), получим
 ,
,
т.е. система (3.5) принимает вид
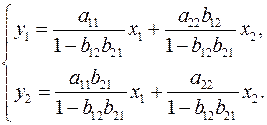
Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели будут выражаться через коэффициенты структурной формы следующим образом:
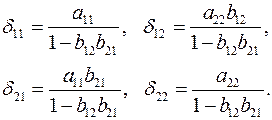
Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.






