При решении уравнений методом касательных в качестве начального приближения к корню выбирается точка 
, для которой выполняется условие 
Как правило, это правый или левый конец отрезка [a, b]. Следующее приближение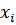 
находится по формуле Ньютона 
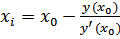. Каждое следующее приближение будет расположено все ближе и ближе к искомой точке (корню). Вычисления прекращаются тогда, когда для найденного значения 
выполняется условие 
.
Проверим выполнение условия для левого и правого конца отрезка, содержащего корень уравнения, который был отделен ранее, в методе бисекций. Как следует из листа «Отделение корней»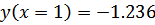 
, 
, 
, 
. Очевидно, что условие выполняется для правого конца отрезка, следовательно, в качестве начального приближения к решению выберем 
Оформите заголовок таблицы в соответствии с примером, показанным на рисунке 5.
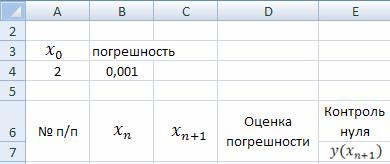
Рисунок 5 – Образец оформления таблицы решения уравнения
В ячейке В8 установите ссылку на А4. В ячейку С8 – запишите формулу вычисления 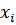. Для нашей функции формула должна выглядеть следующим образом: 
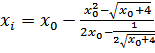. В данном случае 
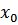берется из ячейки В8. В следующей строке 
- это 
с предыдущей строки. В столбце D укажите условие прекращения вычисленийпо формуле, как это было показано выше. При выводе значения корня уравнения, округлите его до четырех знаков после запятой с помощью функции ОКРУГЛ(). В столбце Е для подтверждения того, что в корне 
вычислим соответствующее значение функции 
.
В результате выполнения работы таблица должна приобрести вид, как показано на рисунке 6.
Рисунок 6 - Пример решения нелинейного уравнения методом касательных
Приближенное решение уравнениЙ 
КОМБИНИРОВАННЫМ методом ХОРД И КАСАТЕЛЬНЫХ
Цель работы: определить корень уравнения, приведенного в задании, используя комбинированный метод хорд и касательных, средствами MS EXCEL.
Задание: найти корень уравнения 
с точностью ε=0,001.
