Изопроцессом называется процесс, при котором один из параметров термодинамической системы остается постоянным. Связь между параметрами системы дает уравнение Менделеева – Клапейрона.
Изотермический процесс (Т = const).
В этом случае уравнение состояния имеет вид:
PV = const
Для нескольких конкретных состояний газа можно записать:
P 1 V 1 = P 2 V 3 =..., = P n V n
График изотермического процесса (изотерма) в координатах P – V изображается гиперболой (рис.2.7).
Подставляя 
из формулы (2.1) в формулу работы (2.23), получим для изотермического процесса:
. (2.38)
Работа изотермического процесса на рис.2.7 численно равна площади под кривой 1-2.
Из формулы 2.29 следует, что изменение внутренней энергии при dT = 0 в изотермическом процессе равно 0. Тогда первый закон термодинамики применительно к изотермическому процессу примет вид Q = A.
Рис.2.7
Т.е. система: либо, получая тепло от внешней среды, совершает работу, расширяясь, либо отдает тепло внешней среде вследствие того, что внешние тела совершают над ней работу, сжимая ее. Следовательно, для того, чтобы при изотермическом расширении температура не падала, к газу необходимо подводить количество теплоты, эквивалентное работе расширения. Наоборот, при сжатии система должна отдавать среде количество теплоты, эквивалентное работе сжатия.
Изобарный процесс (Р = const).
Уравнение состояния при Р = const имеет вид
= const или 
График изобарного процесса в координатах Р – V приведен на рис.2.7. Работа при изобарном процессе (см.2.23)
. (2.39)
На графике работа при Р = const численно равна площади прямоугольника под прямой 1-3.
Первый закон термодинамики для изобарного процесса
Q = ΔU + A.
Изохорный процесс ( V = const).
При изохорном процессе уравнение состояния
или 
(2.40)
Поскольку dV = 0, то работа при изохорном процессе равна нулю. Первый закон термодинамики для изохорного процесса имеет вид
Q = ΔU,
т.е. либо вся теплота, сообщаемая системе, идет на увеличение ее внутренней энергии, либо система отдает среде тепло, уменьшая свою внутреннюю энергию.
Адиабатический процесс.
Адиабатическим называется процесс, протекающий без теплообмена с внешней средой (δQ = 0). Близким к адиабатическим являются все быстропротекающие процессы, например, расширение и сжатие горючей смеси в двигателях внутреннего сгорания.
Учитывая, что δQ = 0, запишем первый закон термодинамики для адиабатического процесса:
А = -ΔU. (2.41)
Отсюда следует, что если газ совершает работу (адиабатически расширяясь), то А>0, соответственно ΔU<0 и ΔТ<0, т.е. газ охлаждается. Наоборот, при адиабатическом сжатии газа А<0, тогда ΔU >0 и ΔТ >0, т.е. газ нагревается.
Используя выражение (2.23) и учитывая, (2.20), перепишем равенство (2.41):
(2.42)
Продифференцируем уравнение Менделеева – Клапейрона (2.1):
. (2.43)
Исключив из уравнений (2.42) и (2.43) температуру Т, получим
или
.
Разделив переменные и учитывая равенство (2.35), найдем
.
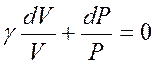Интегрируя это равенство, получим
γlnV + lnP = const.
Или, в окончательном виде, связь между давлением и объемом газа в адиабатическом процессе:
PV γ = const (2.44)
Это отношение называется уравнением адиабаты или уравнением Пуассона. Кривая адиабаты представлена на рис.2.7, которая падает с ростом объема круче, чем изотерма. Это непосредственно следует из того, что γ >1 (см. также формулу 2.35).
Уравнение Пуассона можно выразить и через другие параметры с помощью уравнения Менделеева – Клапейрона
TV γ-1 = const,
T γ P 1-γ = const.
Вычислим работу расширения газа в адиабатическом процессе. Учитывая равенство (2.42), получим
(2.45)
