Уравнение (2.8) имеет универсальный характер, так как в него не входят величины, зависящие от природы газа, и называется основным уравнением молекулярно – кинетической теории.
Воспользуемся формулой (2.4) и определим среднюю квадратичную скорость. Так как
,
то
(2.9)
Статистические закономерности не определяются начальными условиями. Они не дают возможности определить скорость «меченой» молекулы в данный момент времени, но позволяют вычислить долю молекул газа при данной температуре, имеющих скорости, лежащие в интервале значений от V до (V + dV).
На основании теории вероятности Максвелл получил закономерность, по которой можно определить число молекул газа dN, скорости которых при данной температуре заключены в некотором интервале скоростей от V до (V + dV).
dN = F(v,T,m)dV,
где F(v,T,m)– называется функцией распределения.
Максвелл вывел аналитическое выражение функции F(v,T,m):
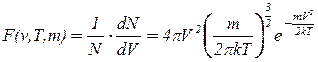, (2.10)
где N – общее число молекул газа;
Т – абсолютная температура;
V – скорость молекулы;
k – постоянная Больцмана;
m – её масса.
Кривая Максвелла имеет максимум, которому соответствует скорость, называемая наиболее вероятной скоростью Vв. Чтобы получить выражение Vв, надо взять первую производную от F(v,T,m) по V и приравнять её к нулю, тогда получим:
=0
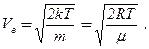(2.11)
Как видно из уравнений, конкретный вид кривой и величина Vв зависит лишь от массы молекулы m и температуры Т. На Рис.2.2 приведены расчётные зависимости плотностей вероятностей обнаружения молекул кислорода (слева) и атомов гелия (справа) для температуры 300К.
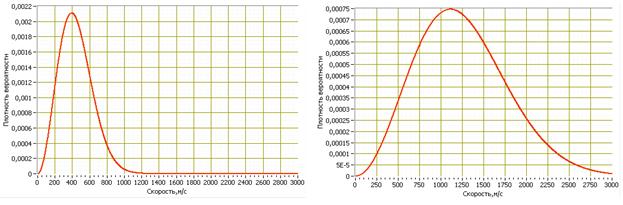
Рис.2.2
Экспериментальная проверка распределения Максвелла была выполнена Штерном.
В молекулярно – кинетической теории есть понятие средней арифметическая скорость поступательного движения молекулы:
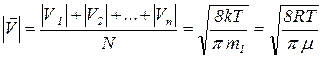(2.12)
где | V1 |, | V2 |, …, | Vn | – скорости отдельных молекул, N – их число; m1 -масса одной молекулы;
С позиций молекулярно – кинетической теории абсолютный нуль температуры по шкале Кельвина соответствует такому состоянию идеального газа, когда движение молекул прекращается и давление Р = 0. Молекулы обладают массой и поэтому должны испытывать гравитационное взаимодействие, как между собой, так и со стороны тяготеющих масс.
Наличие у Земли атмосферы обусловлено как действием на молекулы сил тяготения, так и их тепловым движением. Действие этих факторов приводит к неравномерному распределению молекул в атмосферном слое Земли, при котором давление и концентрация молекул с высотой h над поверхностью Земли убывает.
Пусть давление слоя газа толщиной dh
.
Плотность газа ρ выразим из уравнения Менделеева – Клапейрона (см. раздел 2.1)
.
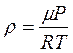Тогда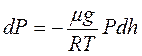 
или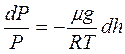 
. Высотам h0 и h соответствуют давления Р0 и Р, т.е.
, 
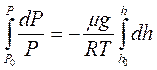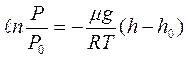
или 
- барометрическая формула.
Давление Р0 на уровне моря считается нормальным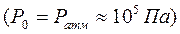 
.
Учитывая, что Р=nkT, можно получить закон зависимости концентрации молекул от высоты h в поле тяготения Земли (распределение Больцмана)
,
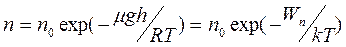где Wn=mgh – потенциальная энергия молекул в поле тяготения (m - масса молекулы).
Таким образом, концентрация молекул в атмосфере Земли убывает (как и давление) с высотой и зависит также от массы молекул (их потенциальной энергии).
