Для однородных дискретных цепей Маркова с непрерывным временем переходные вероятности задаются матрицей P(t):
P(t, i, {j}) = Pij(t)
Введем понятие плотности вероятности перехода lij.

- если существует этот предел, то отсюда следует, что за малое время Dt вероятность Pij(Dt)=lijDt+o(Dt) - бесконечно малая величина более высокого порядка

Предположим, что мы знаем плотности вероятностей перехода lij для всех пар состояний Si, Sj.
Пример.
Построим граф состояний системы S и против каждой стрелки проставим сооответствующую плотность вероятностей перехода. Такой граф с проставленными у стрелок плотностями вероятностей перехода, будем называть размеченным графом состояний.
Оказывается, зная размеченный граф состояний, можно определить вероятности состояний:
p1(t), p2(t),..., pn(t)
как функции времени. Например, найдем вероятность события p1(t). Дадим малое временное приращение Dt и посмотрим, как система попадет в состояние S1.
1) В момент времени t система была в состоянии S1 и осталась в нем. Вероятность этого p1(t)(1-l12Dt)+o(Dt).
2) Система была в состоянии S3 и за время Dt перешла в состояние S1 - вероятность этого события есть p3(t)l31Dt+o(Dt).
3) Вероятность других событий - любых двух и более переходов за время Dt имеют вероятность o(Dt).
В итоге получаем:
p1(t+Dt)= p1(t)(1-l12Dt)+p3(t)l31Dt+o(Dt).
отсюда имеем

Переходя к пределу, имеем
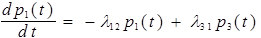
В результате имеем правило:
В левой части каждого уравнения стоит производная вероятностей состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак "минус"; если в состояние - "плюс". Каждый член равен произведению плотности вероятностей перехода, соответствующей данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Пример. В начальный момент времени система находится в состоянии S0.
Пользуясь правилом, получаем следующую систему обыкновенных дифференциальных уравнений:

Имеем условие нормировки p1(t)+p2(t)+p3(t)+p4(t)+p5(t)=1
При t=0 p1=1, p2=p3=p4=p5=0.






