Моделирование операций по схеме марковских процессов
Определение неоднородного марковского процесса.
Пусть имеется фазовое пространство Х. (Для любителей строгости - фазовое пространство - это измеримое пространство (Х, В), в котором все одноточечные множества измеримы). Точки фазового пространства будем называть состояниями.
Пусть имеется случайный процесс xt, tÎTÍR1, со значениями в фазовом пространстве Х.
Случайный процесс xt называется марковским, если
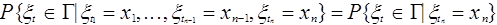
Здесь Г - измеримое множество из Х (т.е. событие), t1<t2<... <tn<t - моменты времени из Т.
Одна из формулировок.
При известном настоящем будущее марковского процесса не зависит от прошлого.
Другая формулировка.
Поведение марковского процесса зависит от последнего состояния, в которое он попал, и не зависит от того, каким способом марковский процесс попал в это состояние.
Определение.
Переходной функцией марковского процесса называется функция Р(s, x, t, Г), удовлетворяющая условию
P{xtÎG|xs}=P(s, xs, t, G)
Это распределение вероятностей на фазовом пространстве, обладающее следующими свойствами:
P(s, x, s, G)=dx(G); здесь dx(G)=1, если xÎG и dx(G)=0 в противном случае;
P(s, X, t, X)=1.
Пусть Р0 - начальное распределение (вероятностная мера) на фазовом пространстве Х, т.е. в начальный момент времени
P{xsÎG}=P0(G)
Тогда, зная переходную функцию, мы можем вычислить любые конечномерные распределения марковского процесса. Действительно:
Если в начальный момент времени s процесс xs исходит из состояния x, то сооответствующее начальное распределение будем обозначать Ps,x и получим
Ps,x(xtÎG)= P(s, x, t, G)
Общая формула
Как частный случай, получаем уравнение Чепмена-Колмогорова. Пусть s£t£u. С одной стороны
Ps,x(xuÎG)= P(s, x, u, G)
с другой стороны
В результате имеем
(ЧК)
Для марковских процессов на несчетном фазовом пространстве (например X=R) иногда имеет смысл говорить о плотности вероятности перехода или переходной плотности p(s, x, t, y), такой, что
Уравнение Чепмена-Колмогорова для переходных плотностей выглядит следующим образом:
(ЧК-2)
