1. Найти линейную комбинацию векторов 
 :
:
а)  ;
;
б)  .
.
Решение:
а) 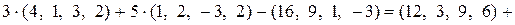
 .
.
2. Найтивектор 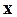 , для которого выполняются условия:
, для которого выполняются условия:
а)  где
где 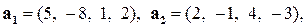

б)  где
где 
 .
.
Решение:
а) Подставим в выражение координаты данных векторов:  .
.
Выполним скалярное умножение и представим  как вектор с координатами
как вектор с координатами  :
:



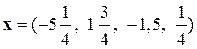 .
.
б) Пусть  . Подставим в выражение координаты данных векторов:
. Подставим в выражение координаты данных векторов: 

Выполнив скалярное умножение, получим систему уравнений:
 .
.
Следовательно,  .
.
3. Описать линейные оболочки системы векторов:
а)  ; б)
; б)  ;
;
в) 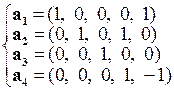 ; г)
; г)  .
.
Решение:
а) 
 – система векторов, у которой вторая и четвертая координаты равны 0.
– система векторов, у которой вторая и четвертая координаты равны 0.
в) 
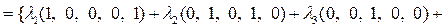
 – система векторов, у которой четвертая координата зависит от второй, пятая – от первой и четвертой.
– система векторов, у которой четвертая координата зависит от второй, пятая – от первой и четвертой.
4. а)Доказать, что система векторов, содержащая два одинаковых вектора, линейно зависима.
б) Доказать, что система векторов, содержащая два пропорциональных вектора, линейно зависима.
Решение:
а) Пусть  – система векторов. Учитывая условие задачи, рассмотрим
– система векторов. Учитывая условие задачи, рассмотрим  . Составим линейную комбинацию этой системы:
. Составим линейную комбинацию этой системы: 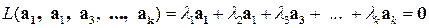 , где
, где  и не все
и не все  равны 0.
равны 0.
Например,  , то есть
, то есть  , значит, система векторов
, значит, система векторов  линейно независима.
линейно независима.
5. 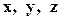 -линейно независимая система векторов. Определить будут ли линейно зависимыми или линейно независимыми следующие системы:
-линейно независимая система векторов. Определить будут ли линейно зависимыми или линейно независимыми следующие системы:
а)  ;
;
б)  .
.
Решение:
а) Составим линейную комбинацию системы векторов  и выясним, при каких
и выясним, при каких  она обращается в
она обращается в  :
: 


Таким образом, получили, что  – линейно независимая система векторов.
– линейно независимая система векторов.
6. Будет ли система векторов  из
из  , где
, где  , линейно зависимой или линейно независимой?
, линейно зависимой или линейно независимой?
Решение:
Составим линейную комбинацию системы векторов  и выясним, при каких
и выясним, при каких  она обращается в
она обращается в  :
:
 .
.
Решим систему уравнений:
 .
.
Значит,  – линейно независимая система векторов.
– линейно независимая система векторов.
7. Проверить будет ли система векторов  , где
, где 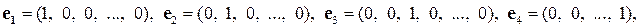 линейно независимой или линейно зависимой.
линейно независимой или линейно зависимой.
Решение:
Данная система векторов называется системой единичных векторов n-мерного векторного пространства. Составим линейную комбинацию системы векторов  и выясним, при каких
и выясним, при каких  она обращается в
она обращается в  :
: 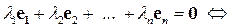

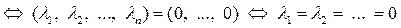 .
.
Следовательно,  – линейно независимая система векторов.
– линейно независимая система векторов.






