1) Система векторов, содержащая нулевой вектор, линейно зависима.
Доказательство.
. Выбираем 
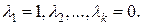
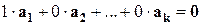
Не все скаляры нулевые, и линейная комбинация равна нулевому вектору, значит система линейно зависима.
■
2) Если какая-нибудь подсистема системы векторов линейно зависима, то и сама система линейно зависима.
Доказательство.
Пусть 
-система векторов. Возьмем подсистему: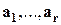 
; 
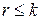. Пусть она линейно зависима, т.е. существуют 
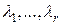, не все равные нулю, и 
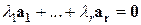. Отсюда следует, что 
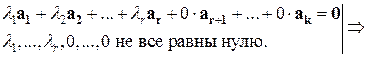система векторов линейно зависима.
■
3) Любая подсистема линейно независимой системы линейно независима.
Доказательство.
Предположим противное, что в системе векторов существует линейно зависимая подсистема. Тогда по свойству 2 - линейно зависимая система. Получили противоречие, которое доказывает свойство 3.
■
4) Система векторов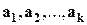 
, где 
, линейно зависима тогда и только тогда, когда один из векторов этой системы является линейной комбинацией предшествующих векторов.
Доказательство.
Необходимость. Пусть линейно зависимая система векторов, тогда существуют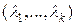 
, такие, что 
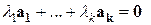и не все 
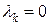. Пусть 
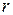- наибольший индекс, такой, что скаляр 
. Тогда из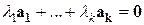 
следует, что 
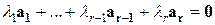значит 
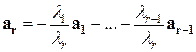. Получили, что 
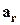- линейная комбинация предшествующих векторов.
Достаточность. Пусть 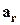- линейная комбинация векторов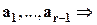 
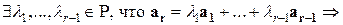
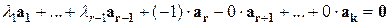. Выпишем коэффициенты: 
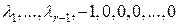- не все 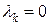, поэтому система векторов линейно зависима.
■
5) Если система векторов - линейно независима, а система векторов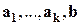 
- линейно зависима, то вектор 
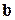- линейная комбинация векторов .
Доказательство.
Рассмотрим линейно зависимую систему векторов 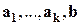. По свойству 1) один из векторов этой системы является линейной комбинацией предшествующих. Никакой из векторов , 
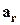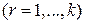, не может быть линейной комбинацией, так как - линейно независимая система по условию. Значит, 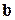является линейной комбинацией предшествующих векторов, т.е. векторов .
■
