; 
, (1.6)
Роторно-опорные узлы представляют собой единую колебательную систему, резонансные явления в которой зависят от жесткости валов и опор. В инженерных расчетах податливостью подшипников качения часто пренебрегают, поэтому динамический анализ сводится к определению критических частот валов. В реальности любой ротор представляет собой систему с распределенной массой и переменной жесткостью, для расчета критических частот nкр которой применяются специальные методы. В первом приближении значения первой критической частоты предположим, что масса вала и присоединенных масс условно сосредоточена в точке, тогда
, (1.7)
где m – приведенная масса вала, которую можно найти с использованием значений масс дисков 
и массы вала 
, например по методу Релея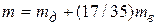 
; С – изгибная жесткость вала.
Применительно к данной работе можно переписать формулу 1.7 в виде
. (1.8)
В действительности ротор имеет бесконечное число критических частот и соответствующих им форм колебаний (рис. 1.2). На практике наибольшее значение имеют первые три частоты. Валы разделяют на жесткие (докритические) и гибкие (закритические). В общем виде условие виброустойчивости можно записать
, (1.9)
где 
- коэффициенты запаса, которые могут принимать значения в диапазоне 
; 
в зависимости от вида роторной машины.
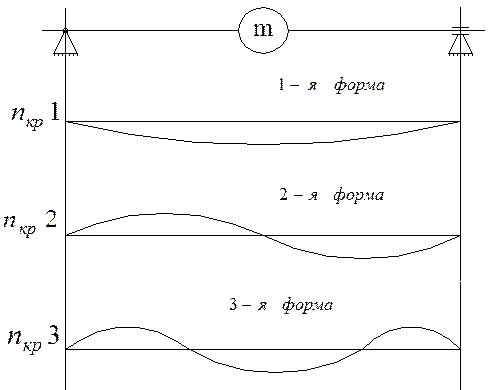
Рис 1.2. Формы колебаний
Физический смысл выполнения критерия виброустойчивости заключается в том, что рабочие частоты не должны находиться в зоне резонанса (рис. 1.3), так как в этом случае возможно разрушение ротора. Материал валов обладает демпфирующей способностью, что позволяет при определенных условиях переходить в зарезонансную зону.
Центр масс ротора всегда смещен относительно оси вращения на величину эксцентриситета e (OO1 на рисунке 1.4), т.е. имеет место дисбаланс. При вращении вследствие неуравновешенности появляется центробежная сила 
, вызывающая прогиб вала. Вращение изогнутой оси вала называется прецессией, которая в зависимости от величины собственной угловой скорости может быть синхронной и несинхронной, прямой и обратной. В зависимости от расположения масс вдоль оси различают дисбаланс силовой и моментный. Для уменьшения дисбаланса проводят балансировку высокоскоростных роторов на специальных станках. Причем точная балансировка проводится для роторов совместно с подшипниками.
Рис. 1.3. Амплитудно-частотная характеристика
Величину динамического прогиба (рис. 1.4) можно определить из условия равенства сил инерции и упругости
, (1.10)
которое с учетом выражения (1.7) принимает вид
. (1.11)
При n < nкр. с увеличением скорости вращения происходит рост динамического прогиба. При резонансе (n = nкр.) наблюдается резкий рост амплитуд и формально 
(рис. 1.3).В закритической зоне (n > nкр.) происходит уменьшение прогиба. Это явление называется самоцентрированием вала. В этом случае nкр. /n становится меньше 1, и значение динамического прогиба 
меняет знак на противоположный, что означает его уменьшение.
| 
|
Рис. 1.4. Схема ротора
