x y
3.00 4.00
7.00 10.00
11.00 22.00
15.00 26.00
19.00 33.00
Точка iнтерполяцii 13.000
Многочлен Ньютона
0.004x^ 4-0.183x^ 3+2.768x^ 2-14.087x+25.958
Значення в точцi iнтерполяцii=24.898
Виконання інтерполяції за допомогою пакету MathCad
ЧИСЕЛЬНЕ ІНТЕГРУВАННЯ ФУНКЦІЙ
Якщо функція f неперервна на відрізку [a;b] і відома її первісна F (F’(x)=f(x)), то справедлива формула Ньютона-Лейбніца:
.
Проте цією формулою важко і навіть практично неможливо скористатися тоді, коли первісну F не можна виразити в елементарних функціях або коли підінтегральну функцію задано графічним чи табличним способом.
У цих випадках треба будувати формули для наближеного обчислення визначених інтегралів. Особливо важливе значення мають методи чисельного інтегрування функцій, в яких для знаходження наближеного значення визначеного інтегралу використовуються значення підінтегральної функції та її похідних у скінченній кількості точок, що належать переважно проміжку інтегрування. Такі формули обчислення наближеного значення визначених інтегралів називають формулами механічних квадратур або квадратурними формулами.
В даному розділі розглянуті три методи чисельного інтегрування: метод прямокутників, метод трапецій, метод Сімпсона. Обчислено один визначений інтеграл всіма трьома методами. Для порівняння, те ж завдання виконане засобами пакету MathCad.
Метод прямокутників
Нехай потрібно обчислити інтеграл 
. Розіб’ємо ділянку інтегрування [a;b] на n рівних частин і помістимо точки, значення функції в яких входять до інтегральної суми, в лівих кінцях одержаних ділянок. Якщо вважати, що n достатньо велике, тобто довжина ділянок розбиття h= 
достатньо мала, то інтегральна сума повинна вже мало відрізнятися від величини інтегралу. Таким чином, ми одержимо наближену рівність:
» h( 
Ця формула називається формулою прямокутників (точніше, формулою лівих прямокутників). Якщо помістити точки, значення функції в яких входять до інтегральної суми, в правих кінцях одержаних ділянок, одержимо формулу правих прямокутників
» h( 
Якщо помістити точки, значення функції в яких входять до інтегральної суми, в серединах одержаних ділянок, одержимо формулу середніх прямокутників
» h(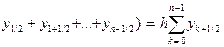 
Програмна реалізація всіх трьох модифікацій методу практично однакова.
Завдання. Методом прямокутників знайти 
Програмна реалізація
Здійснена на мові С.
