r[0]=0.000
r[1]=0.000
r[2]=0.000
ІНТЕРПОЛЮВАННЯ ФУНКЦІЙ
Нехай на відрізку [a;b] визначено певний клас функцій {P(x)}, наприклад, клас алгебраїчних многочленiв, а в точках x0,x1,...,xn цього проміжку задано значення деякої функції y=f(x): y0=f(x0), y1=f(x1),..., yn=f(xn). Наближену заміну функції f на відрізку [a;b] однією з функцій P(x) цього класу так, щоб функція P(x) в точках x0,x1,...,xn набувала тих самих значень, що й функція f, називають інтерполюванням або інтерполяцією. Точки x0, x1,...,xn називають вузлами інтерполювання, функцію P(x) - інтерполюючою функцією, а формулу f(x)»P(x), за допомогою якої обчислюють значення функції f у проміжку [a;b], - інтерполяційною формулою.
Якщо функція P(x) належить до класу алгебраїчних многочленiв, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати та інтегрувати.
Сформулюємо задачу параболічного інтерполювання: в n+1 різних точках x0, x1,...,xn задано значення функції f: y0=f(x0), y1=f(x1),..., yn=f(xn) і треба побудувати многочлен
Pn(x)=a0xn+a1xn-1+...+an-1x+an
степеня n, який задовольняв би умови:
Pn(xi)=yi (i=0,1,..., n).
Задача має єдиний розв’язок. Многочлен Pn(x) називають інтерполяційним многочленом. Інтерполяційний многочлен єдиний, проте можливі різні форми його запису.
Інтерполяційний многочлен будують тоді, коли:
функцію задано таблично для деяких значень аргументу, а треба знайти її значення для значень аргументу, яких в таблиці нема.
функцію задано графічно, а треба знайти її наближений аналітичний вираз.
функцію задано аналітично, але її вираз досить складний і незручний для виконання різних математичних операцій.
При написанні даної роботи розглядалася перша задача - чисельної інтерполяції.
Інтерполяційний многочлен Лагранжа
Інтерполяційний многочлен Лагранжа має такий вираз:
Ln(x)= 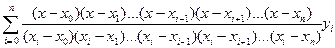
Многочлен Лагранжа зручно будувати у випадку рівновіддалених вузлів.
Завдання. Задане табличне представлення функції:
| x | |||||
| y |
Методом інтерполяції Лагранжа знайти значення функції при x=13.
Програмна реалізація
Здійснена на мові С.






