Каждой квадратной матрице по определенному правилу можно поставить в соответствие единственное число – определитель (determinant).
Если А – матрица, то определитель обозначают:
или 
или 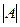буквой 
(дельта).
Если задана матрица 1-го порядка 
. Для нее определитель 
.
Если задана матрица 2-го порядка 
, то определителем второго порядка числовой матрицы А называется число
.
Если задана матрица 3-го порядка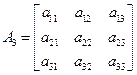 
, то определителем третьего порядка числовой матрицы А называется число
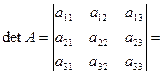
Такой метод вычисления определителя 3-го порядка называется правилом треугольников (или правилом Саррюса). Схематическая запись этого правила имеет вид:
+ –
.
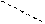
Свойства определителей:
1) 
;
2) если поменять местами две строки (два столбца) определителя, то его знак измениться на противоположный;
3) если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю;
4) определитель с двумя пропорциональными (в частности равными) строками (столбцами) равен нулю;
5) общий множитель всех элементов строки (столбца) можно выносить за знак определителя;
6) определитель не изменится, если к элементам одной строки прибавить элементы другой строки, умноженные на любое ненулевое действительное число.
7) определитель произведения матриц А, В равен произведению определителей этих матриц, т.е.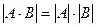 
.
Следствие: 
.
Определитель называется треугольным (диагональным), если он записан для треугольной (диагональной) матрицы. Он равен произведению элементов главной диагонали.
Используя свойства определителей, получаем другие способы их вычисления:
1) зануление всех элементов определителя в строке (столбце), кроме одного;
2) приведение определителя к треугольному виду.
