Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной; обозначается 
. 
.
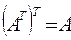Операция умножения матриц определена только для согласованных матриц.
Матрицы А и В называют согласованными, если число столбцов матрицы А равно числу строк матрицы В, например 
и 
.
Произведением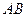 
согласованных матриц
и 
называется матрица С
.
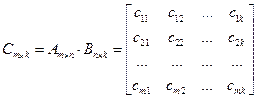Чтобы вычислить элемент 
матрицы С нужно перемножить попарно и последовательно перемножить все элементы 
й строки матрицы А и 
го столбца матрицы В и сложить их, т.е.
,
,
……………………………………..,
,
,
……………………………………,
,
,
……………………………………….,
.
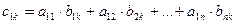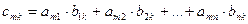Произведение матриц в общем случае не обладает свойством коммутативности, т.е. не всегда 
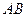. Если определено , это еще не означает, что определено 
.
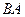Если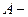 
квадратная матрица, то 
й степенью матрицы А (обозначается 
) называется произведение 
.
При 
полагают 
.
Если 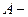квадратная матрица порядк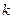а 
, а 
– многочлен степени 
, то многочленом 
й степени от матрицы А называется матрица
.