1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряжённостью 
. Со стороны поля заряд 
испытывает действие силы 
и приобретает ускорение 
. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
где 
- среднее время между двумя последовательными соударениями электрона с ионами решётки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решётки, отдаёт им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно средняя скорость направленного движения электрона
. (1)
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время свободного пробега определяется средней длиной свободного пробега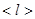 
и средней скоростью движения электронов относительно кристаллической решётки проводника, равной 
(
- средняя скорость теплового движения электронов). Ранее было доказано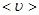 
<< , поэтому
.
Подставив значение в (1), получим:
Плотность тока в металлическом проводнике
, (2)
откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получили закон Ома в дифференциальной форме. Коэффициент пропорциональности между 
и 
есть не что иное, как удельная проводимость материала
, (3)
которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.
2. Закон Джоуля – Ленца. К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию
(4)
При соударении электрона с ионом эта энергия полностью передаётся решётке и идёт на увеличение внутренней энергии металла, т. е. на его нагревание.
За единицу времени электрон испытывает с узлами решётки в среднем 
столкновений:
(5)
Если n – концентрация электронов, то в единицу времени происходит 
столкновений и решётке передаётся энергия
, (6)
которая идёт на нагревание проводника. Подставив (4), (5) в (6) получим таким образом энергию, передаваемую решётке в единице объёма проводника за единицу времени,
. (7)
Величина 
является удельной тепловой мощностью тока. Коэффициент пропорциональности между и 
по (3) есть удельная проводимость 
; следовательно, выражение (7) – закон Джоуля –Ленца в дифференциальной форме.
3. Закон Видемана-Франца. Видеманом и Францем экспериментальноустановлен закон, согласно которому отношение теплопроводности 
к удельной проводимости 
для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре:
,
где 
- постоянная, не зависящая от рода металла.
Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля – Ленца, а также дала качественное объяснение закона Видемана – Франца.
