Ток, который меняется со временем по величине и по направлению, называется переменным.
Примеры:
Синусоидальные токи получили распространение, так как они выгодны при передаче и трансформации. Они меньше всего меняют свою форму. Способ получения основан на законе Фарадея. Рамка (см. рис) вращается с постоянной угловой скоростью 
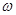, т. е. 
, 
. Поток магнитной индукции будет меняться по закону: 
. В рамке возникает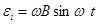 
, где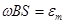 
или амплитуда, 
- фаза.
Если посредством скользящих контактов подсоединим замкнутую цепь, то:
.
На этом принципе основано действие генератора, синхронного двигателя.
Действующее значение переменного синусоидального тока – это такое значение постоянного тока, при прохождении которого в одном и том же резисторе за время одного периода 
выделяется столько же теплоты, как и при синусоидальном токе.
, 
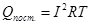
- действующее или эффективное значение тока. Действующее значение является среднеквадратичным значением.
.
Среднее значение – значение постоянного тока, при котором за пол периода переносится такой же заряд, как и при синусоидальном токе.
,
.
Коэффициент формы периодической кривой – это отношение к действующего значения тока к значению среднего тока.
.
Для синусоидального тока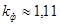 
.
Способы представления синусоидальных токов.
,
,
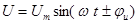
- в электротехнике. Здесь 
- начальная фаза, характеризует момент времени, прошедший от начала колебаний.
Пусть 
, 
, т. е. 
от 
отличается по фазе на . 
- ток и напряжение совпадают по фазе.
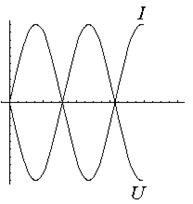
ток и напряжение в противофазе –
- сдвиг фаз между током и напряжением ( отстаёт от ).
Отстаёт по фазе та из двух величин, которая при переходе от отрицательного значения к положительному позже (правее) пересекает ось абсцисс.
Положение точки на плоскости можно охарактеризовать вектором и углом, т. е. можно представить векторно. Взаимное расположение точек не меняется и взаимная ориентация векторов не меняется сдвиг по фазе остаётся неизменным. Отсюда вытекает метод векторных диаграмм:
Задаётся один из векторов, например ток. В зависимости от схемы может получиться опережение или отставание. Принято опережение считать против часовой стрелки (см. рис.).
Если есть несколько токов или напряжений, то напряжения и токи складываются отдельно по правилу сложения векторов. Это метод анализа.
Комплексный метод.
,
где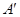 
- действительная и 
- мнимая части, 
.
,
,
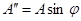
где - аргумент комплексного числа, 
- его модуль.
Используя формулу Эйлера:
.
Здесь 
- поворотный множитель.
, 
, 
.
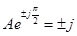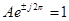Поворот вектора OA на угол 
эквивалентен умножению его на 
. Поворот на угол заменяется умножением. При дифференцировании синусоидальной функции, изображение в комплексном виде превращается в умножение.
Комплексное число, изображающее производную синусоидальной функции, равно комплексному числу, изображающему саму функцию, умноженную на 
.
к.ч.,
к.ч. 
.
Интегрирование сводится к делению на .
,
.
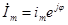Рассмотрим отдельно каждый из элементов R, L, C.
 | |||
 | |||
1) Активное сопротивление не оказывает влияния на входные характеристики входного сигнала (рисунок справа).
.
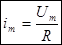
т. е. сдвиг фаз между током и напряжением равен нулю.
2) 
.
.
Согласно закону Кирхгофа:
.
Разделяя переменные, получим:
,
.
 |
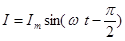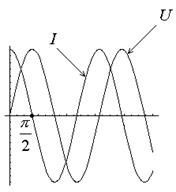Векторная диаграмма для этого случая:
Здесь ток отстаёт от напряжения по фазе на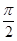 
из-за явления самоиндукции.
