Блок-схема экспериментальной установки представлена на рис. 2. Она состоит из: генератора G симметричных импульсов напряжения треугольной формы; образцового сопротивления R; двух исследуемых соленоидов L 1и L 2, включаемых по выбору переключателем SA 2и электронного осциллографа ЭО.
Генератор G задает симметричные импульсы напряжения треугольной формы (рис. 3а), имеющие различную частоту (для задания частоты служит переключатель SA 1).
 Электронный осциллограф служит для наблюдения формы и измерения величины сигналов напряжения на образцовом сопротивлении и на соленоиде, подключаемых по выбору переключателем SA3. Треугольным импульсам напряжения на R соответствуют такие же импульсы первичного тока на соленоиде L.
Электронный осциллограф служит для наблюдения формы и измерения величины сигналов напряжения на образцовом сопротивлении и на соленоиде, подключаемых по выбору переключателем SA3. Треугольным импульсам напряжения на R соответствуют такие же импульсы первичного тока на соленоиде L.
Импульсы тока треугольной формы характерны тем, что на участках нарастания и убывания тока (рис. 3 а) скорости изменения силы тока постоянны, одинаковы по величине, но имеют разные знаки. Поэтому ЭДС самоиндукции приобретает значения то 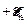 , то
, то  ,т.е. теоретически образует импульсы прямоугольной формы (рис. 3 б). Для вычисления индуктивности L из формулы для самоиндукции надо знать ЭДС
,т.е. теоретически образует импульсы прямоугольной формы (рис. 3 б). Для вычисления индуктивности L из формулы для самоиндукции надо знать ЭДС  и скорость
и скорость  .
.
 Значение
Значение  определяют по вертикальной шкале на экране осциллографа с учетом цены деления шкалы, заданной при настройке осциллографа. Для измерения
определяют по вертикальной шкале на экране осциллографа с учетом цены деления шкалы, заданной при настройке осциллографа. Для измерения  осциллограф подключают к соленоиду переключателем SA3.
осциллограф подключают к соленоиду переключателем SA3.
Скорость изменения силы тока в треугольном импульсе находят, измерив осциллографом максимальное изменение напряжения U на образцовом сопротивлении R и зная заданную частоту ν следования импульсов (рис. 3 а):
 ,
,
выразив период как 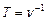 . Значение R указано на установке.
. Значение R указано на установке.
Задавая переключателем SA1 различную частоту следования треугольных импульсов, можно убедиться в справедливости закона электромагнитной индукции в широком диапазоне скоростей изменения первичного тока, а также более точно вычислить индуктивность L соленоида.
Поскольку амплитуда треугольных импульсов тока в установке автоматически поддерживается постоянной на всех частотах, ЭДС самоиндукции прямо пропорциональна частоте  . Коэффициент пропорциональности k определяется статистическим методом наименьших квадратов. Далее вычисляется индуктивность соленоида по формуле
. Коэффициент пропорциональности k определяется статистическим методом наименьших квадратов. Далее вычисляется индуктивность соленоида по формуле  . Цель метода наименьших квадратов найти такое значение коэффициента k в уравнении прямой
. Цель метода наименьших квадратов найти такое значение коэффициента k в уравнении прямой 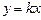 , построенной на основе n экспериментальных точек, чтобы сумма ординатных отклонений экспериментальных точек от расчетной прямой была минимальной:
, построенной на основе n экспериментальных точек, чтобы сумма ординатных отклонений экспериментальных точек от расчетной прямой была минимальной:  . Из условия минимума
. Из условия минимума  получаем расчетную формулу
получаем расчетную формулу  .
.






