Обработка результатов. Точность графического определения ЭДС (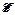 ) и внутренне­го сопротивления ( ) низка, поэтому для получения более точных результатов применяют математический

Точность графического определения ЭДС () и внутренне­го сопротивления () низка, поэтому для получения более точных результатов применяют математический метод наименьших квадратов. Этот метод позволяет подобрать такие значения пара­метров а и b прямой, проходящей через n экспериментальных то­чек, чтобы сумма квадратов ординатных отклонений этих точек от расчетной была минимальной:

.

Из условий минимума функции двух переменных

, ,

получаются формулы, для расчета величин a и b:

,

.

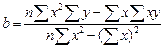По этим формулам находят ЭДС E = а и внутреннее сопротивление r = - b.

Для расчетов составляют таблицу:

Номер опыта	I, A	, Ом	, А-1
...
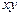
n =

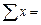
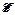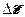Исходные величины и определены с достаточно высо­кой точностью. Класс точности магазина сопротивлений равен 0,2. Это значит, что любое сопротивление, установленное на ма­газине, выдается с погрешностью не более 0,2 %. Существует разброс экспериментальных точек и поэтому существуют вариации в значениях и . Расчет и 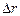, согласно теории метода наименьших квадратов, ведется по форму­лам:

, , ,

, ,

, .

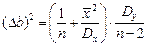Окончательный результат работы представляют в виде: 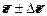, ,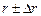а также указывают относительные погрешности (выра­женные в %). По указанию преподавателя некоторые студенты могут не выполнять расчета и 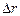.