Наиболее выгодными условиями для проведения измерений физической величины являются такие, при которых получается минимальная погрешность.
При использовании электроизмерительных приборов наименьшая ошибка будет в случае использования последней четверти шкалы; в этом случае она приближается к приведенной ошибке (для погрешности).
В случае косвенных измерений можно определить интервалы значений величин, подлежащих непосредственному измерению, при которых данный метод измерений дает наибольшую точность, т. е. наименьшие ошибки измерений величины
.
Для этого записывается выражение для относительной ошибки
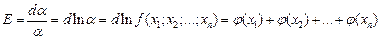
Это выражение, как мы уже видели выше, является суммой частных производных (или как их иногда называют, частных ошибок), являющихся некоторыми функциями измеряемых величин 
.
Определяем, при каких значениях каждая из этих частных производных является минимальной, т. е. дает наименьший вклад в общую ошибку. Для этого берем первую и вторую производную от 
.
Приравнивая к нулю 
находим значения 
.
Если при этом выполняется условие, что
,
то наиболее выгодными условиями для измерения величины α будут такие, когда значения величин 
будут приближаться к 
.
Непосредственный анализ выражения для относительной ошибки позволяет оценить минимальную погрешность.
Например, в гальванометре с магнитной стрелкой сила тока I и угол отклонения магнитной стрелки φ связаны соотношением
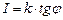, где k - константа
В этом случае видно, что минимальная ошибка будет при максимальном значении знаменателя, при значении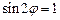 
или при 
=45°.
Значит, наибольшей чувствительностью прибор обладает при углах отклонения порядка 45°.
В других случаях приходится учитывать некоторые зависимости между непосредственно измеряемыми величинами.
Например, при измерении удельного сопротивления материала образца компенсационным методом. Для значения относительной ошибки было получено следующее значение
.
Частная ошибка 
определяется погрешностью эталонного сопротивления и обычно бывает невелика. Ошибки 
и 
связаны с геометрическими размерами образца, с точностью их измерения и не меняются в условиях опыта. Остаются ошибки 
и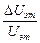 
. Абсолютные ошибки 
и 
определяются точностью потенциометрического мостика. Таким образом, на первый взгляд кажется, что для получения наиболее выгодных условий измерения (для получения наименьших ошибок) необходимо брать наибольшие значения 
и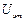 
. Этого можно достичь при увеличении рабочего тока (см. рис. 9), протекающего через образец и эталонное сопротивление.
В целом ряде случаев необходимо, чтобы при измерениях через образец пропускался минимальный ток. Задача решается, если обратить внимание на связь , 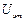ивеличины проходящего тока 
.
Если в цепи поддерживать постоянным ток , то будет постоянным и внешнее падение напряжения, равное сумме и 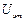(пренебрегая падением напряжения на соединительных проводах):
.
Тогда относительная ошибка, связанная с измерением напряжений:
.
Так как измерения и 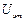производятся на одном приборе, то
и 
.
Обозначим 
и найдём первую и вторую производные
.
Условие 
удовлетворяется при всех значениях так как 
и 
(рассматривается абсолютное значение).
Решая уравнение 
, получим 
, а поскольку , то 
.
Таким образом, для получения наименьших ошибок при измерении удельного сопротивления компенсационным методом, необходимо эталонное сопротивление подбирать того же порядка, что и измеряемое сопротивление.
