Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения на проводнике:
 .
| (3.1) |
Под однородностью понимается отсутствие сторонних сил. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении в 
течет ток силой в 
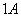. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
 ,
| (3.2) |
где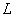 
– длина проводника, 
– площадь поперечного сечения, 
– зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. Удельное сопротивление численно равно сопротивлению единицы длины проводника, имеющего площадь поперечного сечения, равную единице.
Рис. 3.2
|
В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора напряженности электрического поля 
. Поэтому направления векторов 
и совпадают. Найдем связь между и в одной и той же точке проводника. Для этого выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам и (рис. 3.2). Через поперечное сечение цилиндра течет ток силой 
. Так как поле внутри выделенного объема можно считать однородным, то напряжение, приложенное к цилиндру, равно 
, где 
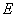– напряженность поля в данном месте. Сопротивление цилиндра, согласно (3.2), равно 
. Подставив эти значения в формулу (3.1), придем к соотношению:
,
откуда
.
Воспользовавшись тем, что векторы и имеют одинаковое направление, можно написать
 .
| (3.3) |
Величина 
называетсяудельной электрической проводимостью материала. Единицей измерения является сименс. Формула (3.3) дает выражение закона Ома в дифференциальной форме, это означает, что она связывает величины, относящиеся к одной точке пространства.
Для участка цепи, на котором действуют сторонние силы, закон Ома запишется в следующей форме:
 .
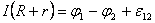| (3.4) |
Перепишем (3.4) в виде
.
Рис. 3.3
|
Эта формула выражает закон Ома для неоднородного участка цепи.
Рассмотрим простейшую замкнутую цепь, содержащую источник тока и нагрузку с сопротивлением R (рис. 3.3). Сопротивлением подводящих проводов пренебрегаем. Положив 
, получим выражение закона Ома для замкнутой цепи:
.
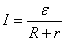Идеальный вольтметр, подключенный к зажимам работающего источника тока, показывает напряжени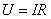е 
, как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. Подставляя силу тока из этого выражения в закон Ома для замкнутой цепи, получаем:
.
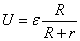Отсюда видно, что напряжение U на зажимах работающего источника всегда меньше его ЭДС. Оно тем ближе к 
, чем больше сопротивление нагрузки R. В пределе при 
напряжение на зажимах разомкнутого источника равно его ЭДС. В противоположном случае, когда R=0, что соответствует короткому замыканию источника тока, U=0, а ток при коротком замыкании максимален: 
.
Закон Ома позволяет рассчитать любую сложную цепь. Разветвленная цепь характеризуется силой токов, идущих по ее участкам, сопротивлениями участков и ЭДС, включенными в эти участки. Сила тока и ЭДС являются величинами алгебраическими, то есть считаются положительными, если электродвижущая сила способствует движению положительных зарядов в выбранном направлении, а ток течет в этом направлении, и отрицательными в противоположном случае. Однако непосредственный расчет разветвленных цепей бывает сложным. Этот расчет значительно упрощается при использовании правил, предложенных Кирхгофом.
