Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.
Следовательно, работа (9.1) равна разности значений потенциальной энергии, которыми обладал заряд q ' в точках 1 и 2 поля заряда q:
Отсюда выражение для потенциальной энергии заряда q ' в поле заряда q
Значение постоянной С выбирается таким, чтобы при удалении заряда на бесконечность (r = ¥) потенциальная энергия обращалась в нуль. При этом условии
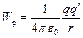(28)
Пусть заряд q ' – пробный заряд. Его потенциальная энергия зависит не только от величины q ', но и от величин q и r, определяющих поле.
Разные пробные заряды 
и т. д. обладают в одной и той же точке поля различной энергией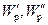 
и т. д. Однако, для данного источника поля q отношение 
будет для всех зарядов одинаковым. Величина
(29)
называется потенциалом поля в данной точке и является энергетической характеристикой электрического поля.
Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Следовательно потенциал поля точечного заряда равен:
Пусть поле создается системой точечных зарядов q 1, q 2... Расстояния от каждого из зарядов до данной точки поля r 1, r 2... Работа, совершаемая силами этого поля над зарядом q ’ равна сумме работ сил, обусловленных каждым из зарядов:
Но каждая из работ А i равна
(30)
где r i1 – расстояние от заряда q i до начального положения заряда q ', r i2 – расстояние от q i до конечного положения заряда q '. Следовательно,
Из сопоставления этого выражения с соотношением
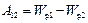
получается выражение для потенциальной энергии заряда q ' в поле системы зарядов
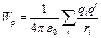
откуда
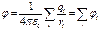
Потенциал поля, создаваемого системой зарядов, равен сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Напряженности поля складываются при наложении полей векторно, потенциалы –алгебраически. Поэтому вычисление потенциалов обычно гораздо проще, чем вычисление напряженностей электрического поля.
Из (29) определяется потенциальная энергия заряда q, находящегося в точке поля с потенциалом j
(30)
Работа сил поля над зарядом q может быть выражена через разность потенциалов:
(31)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.
Если заряд q из точки с потенциалом j удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
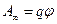(32)
Отсюда: потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Такую же работу необходимо совершить против сил электрического поля, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
За единицу потенциала, называемую вольтом (сокращенное обозначение B), принимается потенциал в такой точке поля, для перемещения в которую из бесконечности положительного заряда 1Кл необходимо совершить работу, равную 1 Дж:
1 дж = 1 к×1 в, отсюда
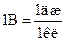(33)
В физике часто пользуются единицей работы и энергии, называемой электронвольтом (эв). Под электронвольтом подразумевается работа, совершаемая силами поля над зарядом электрона при прохождении им разности потенциалов в 1 В:
1 эв=1,6 10-19кл 1 в = 1,6 10-19дж.
Используются также кратные электронвольту единицы:
1 кэв (килоэлектронвольт) = 103 эв,
1 Мэв (мегаэлектронвольт) = 106 эв,
1 Гэв (гигаэлектронвольт) = 109 эв.
Полезно помнить, что величина kT, характеризующая среднюю энергию теплового движения молекул при комнатной температуре, равна
Вопрос 10. Связь между напряженностью электрического поля и потенциалом
Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины j. Между этими величинами должна существовать связь. Так как Е пропорциональна силе, действующей на заряд, а j – потенциальной энергии заряда, понятно, что эта связь должна быть аналогична связи между потенциальной энергией и силой. Работа сил поля над зарядом q на отрезке пути d l представима, с одной стороны, как qEl d l, с другой стороны – как убыль потенциальной энергии заряда 
. Тогда
откуда
ИЛ)
где через l обозначено произвольно выбранное направление в пространстве. В частности,
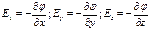Щ-4
откуда
Выражение в скобках называется градиентом скаляра j (см. лекции по механике – связь силы и потенциальной энергии). Обозначается как grad j или с использованием оператора набла: Ñ j. Используя обозначение градиента, можно написать:
E = – grad j AL3)
Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком. Градиент некоторой скалярной функции j (х, у, z) есть векторная величина, обладающая следующими свойствами.
Направление градиента совпадает с направлением n, в котором при смещении из данной точки функция j, возрастая по величине, изменяется с наибольшей скоростью. Величина производной 
по этому направлению дает модуль градиента. Частные производные - 
представляют собой проекции градиента на координатные оси х, у, z. Аналогично производная 
, взятая по произвольному направлению l, есть проекция градиента на это направление. Проекция градиента на перпендикулярное к n направление t, очевидно, равна нулю: 
.
Соотношение между напряженностью поля и потенциалом точечного заряда. Потенциал этого поля равен
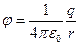
Положение точки поля 1 определяется радиусом - вектором r (рис. 20 выполнен в предположении, что q положителен). При смещении точки из положения1 в разных направлениях на одинаковый по величине малый отрезок d l наибольшее положительное приращение j получается для направления от точки 1 к заряду q, если заряд положителен, и для направления от заряда q к точке 1, если заряд отрицателен. Следовательно, направление градиента n может быть представлено в виде
A1.4)
где знак «–» соответствует случаю положительного заряда, знак «+»– отрицательного. Проекция grad j на направление r равна
Ъ\
Знак «–» в этом выражении указывает на то, что grad j в случае положительного заряда имеет направление, противоположное r, а в случае отрицательного заряда – совпадающее с r. Модуль grad j, очевидно, равен модулю выражения (П.5). Поэтому, с учетом A1.4):
Можно рассмотреть обратную задачу, т. е. по заданным в каждой точке значениям 
найти разность потенциалов между двумя произвольными точками поля. Работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, равна
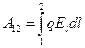
Та же работа может быть представлена в виде
Отсюда
A1.7)
Интеграл в правой части можно брать по любой линии, соединяющей точки 1 и 2, так как работа сил поля не зависит от пути. Для обхода по замкнутому контуру j 1 = j 2 и формула A1.7) переходит в соотношение (9.2).
Разность потенциалов между двумя бесконечными разноименно заряженными плоскостями (однородное поле).
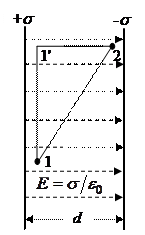
Напряженность поля между ними равна s/e0 и направлена перпендикулярно к плоскостям. Для простоты расчета разности потенциалов между точками 1 и 2, взятыми произвольным образом на разных плоскостях, можно ввести линию 1 – 1'– 2, как показано на рис. 21. Тогда
На участке 1 – 1' El = 0, поэтому первое слагаемое в правой части равно нулю (отсюда следует равенство потенциалов в точках 1 и 1'). На участке 1' – 2 El = Е = const, следовательно,
где d – проекция расстояния между точками 1 и 2 на направление вектора . Таким образом, в однородном поле
A1.8)
В частности, это выражение определяет связь разности потенциалов между пластинами конденсатора с напряженностью поля в конденсаторе. Расстояние между пластинами равно d.
