
где  - напряжение на контуре при частоте w;
- напряжение на контуре при частоте w;
 - напряжение на контуре при резонансе.
- напряжение на контуре при резонансе.
Фазочастотная характеристика:


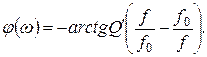
Определив полосу пропускания Sa как ширину резонансной кривой напряжения на уровне  и резонансную частоту
и резонансную частоту  можем найти добротность Q' по соотношению
можем найти добротность Q' по соотношению

Таблица 4.2
| №ВАРИАНТА | 
| 
| 
| 
|
| мкФ | В | к0м | к0м | |
| I | 4.5 | 5.6 | ||
| 5.5 | 5.6 | |||
| 6.5 | 5.6 | |||
| 7.5 | 5.6 | |||
| 8.5 | 5.6 | |||
| 3.5 | 5.6 | 9 |
Домашнее задание
1. Изучить раздел «Резонанс в параллельном контуре».
2. Рассчитать параметры контура 
3. Рассчитать и построить амплитудно-частотную и фазочастотную  характеристики контура для заданного варианта при двух значениях добавочного сопротивления
характеристики контура для заданного варианта при двух значениях добавочного сопротивления  (табл. 4.2).
(табл. 4.2).
Катушка индуктивности, включенная в контур, для всех вариантов имеет параметры  Гн,
Гн,  Ом и содержит 3600 витков. Входное сопротивление генератора синусоидального напряжения мало, и им можно пренебречь. Добавочное сопротивление
Ом и содержит 3600 витков. Входное сопротивление генератора синусоидального напряжения мало, и им можно пренебречь. Добавочное сопротивление 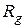 играет роль внутреннего сопротивления эквивалентного источника тока, т.е
играет роль внутреннего сопротивления эквивалентного источника тока, т.е 
Последовательность выполнения работы
1. Собрать схему, представленную на рис.4.13.
2. Снять амплитудно – частотную характеристику контура при 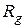 = 5,6 кОм и
= 5,6 кОм и 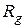 = 9 кОм Для этого, изменяя частоту генератора, по максимуму показаний вольтметра определить резонансную частоту
= 9 кОм Для этого, изменяя частоту генератора, по максимуму показаний вольтметра определить резонансную частоту  контура. Затем, изменяя частоту генератора в обе стороны (больше и меньше) от резонансной, снять показания вольтметра. Причем вблизи
контура. Затем, изменяя частоту генератора в обе стороны (больше и меньше) от резонансной, снять показания вольтметра. Причем вблизи  частоту изменять с небольшим интервалом, затем интервал частот увеличивать. Напряжение генератора U поддерживать постоянным, равным заданному. В процессе эксперимента напряжения
частоту изменять с небольшим интервалом, затем интервал частот увеличивать. Напряжение генератора U поддерживать постоянным, равным заданному. В процессе эксперимента напряжения  и
и  измеряются электронным вольтметром со свободными концами.
измеряются электронным вольтметром со свободными концами.

Рис.4.13
3. Собрать схему (рис.4.14) и снять фазочастотную характеристику параллельного колебательного контура.

Рис.4.14
4. Построить характеристики и сравнить их с расчетными.
5. Вычислить: а) характеристическое сопротивление контура; б) сопротивление контура  при резонансе; в) добротность контура по резонансной характеристике при двух значениях
при резонансе; в) добротность контура по резонансной характеристике при двух значениях  .
.
Основные вопросы к работе
1. Почему резонанс в параллельном колебательном контуре называют резонансом токов? Каково условие резонансов токов?
2. Как определяется волновое сопротивление, резонансная частота и добротность простого параллельного контура (см. рис.4.10)?
3. Построить векторные диаграммы параллельного контура при частотах 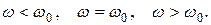
4. Что такое безразличный резонанс, условия его получения?
5. При каких условиях параллельный контур считают контуром с малыми потерями?
6. Как определяется входное сопротивление параллельного контура с малыми потерями?
7. Как зависит добротность параллельного контура от величины внутреннего сопротивления источника?
8. Как зависит полоса пропускания простого параллельного контура от добротности?
Литература
[3], с. 131-138; [6], с. 131-142; [7], с.152-162.
Лабораторная работа №6
ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
Цель работы
Изучение свойств, методов расчета и определение параметров цепи переменного тока при наличии индуктивной связи между элементами цепи.
Основные теоретические положения
Два или более элементов электрической цепи индуктивно связаны, если изменение тока в одном элементе создает ЭДС в другом. Это явление называется взаимоиндукцией, а возникающая при этом электродвижущая сила — ЭДС взаимоиндукции. Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи:
 (6.1)
(6.1)
где М – взаимная индуктивность элементов цепи;
 - индуктивность элементов цепи.
- индуктивность элементов цепи.
Взаимная индуктивность, а следовательно, и коэффициент связи зависят от магнитной проницаемости среды, в которой находятся катушки, от расстояния между катушками и их взаимной ориентации.
В виде примера ниже рассматривается цепь из двух индуктивно связанных катушек, соединенных последовательно с синусоидальным источником ЭДС (рис.6.1, а). Эта цепь описывается уравнением
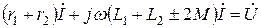 . (6.2)
. (6.2)
Здесь верхний знак (плюс) соответствует согласному, а нижний знак (минус) встречному включению. Отсюда получаем эквивалентные параметры двух индуктивно связанных катушек при последовательном соединении для согласного и встречного включения.
 – эквивалентное активное сопротивление цепи,
– эквивалентное активное сопротивление цепи,
 – эквивалентная индуктивность цепи при согласном включении;
– эквивалентная индуктивность цепи при согласном включении;
 — эквивалентная индуктивность цепи при встречном включении.
— эквивалентная индуктивность цепи при встречном включении.
Вычитая 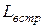 из
из  , можно получить выражение для определения взаимной индуктивности:
, можно получить выражение для определения взаимной индуктивности:
 . (6.3)
. (6.3)
Соотношение (6.3) положено в основу одного из методов экспериментального определения взаимной индуктивности. Используя схему на рис. 6.1,а, измеряют напряжение, приложенное к цепи, и токи при согласном и встречном включениях катушек. Так как  , сопротивление цепи при согласном включении больше, чем при встречном. Поэтому согласное включение катушек соответствует меньшему току, а встречное – большему.
, сопротивление цепи при согласном включении больше, чем при встречном. Поэтому согласное включение катушек соответствует меньшему току, а встречное – большему.
По измеренным величинам вычисляют полные сопротивления цепи при согласном и встречном соединениях:
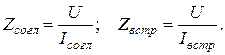
Затем с помощью омметра измеряют активные сопротивления каждой катушки, находят эквивалентное активное сопротивление всей цепи и вычисляют реактивные сопротивления цепи при согласном и встречном включениях:

 (6.4)
(6.4)
По известной частоте источника синусоидального напряжения и реактивным сопротивлениям определяют соответствующие эквивалентные индуктивности
 (6.5)
(6.5)
и по формуле (6.3) вычисляют взаимную индуктивность М.

Рис.6.1

Рис.6.2
Векторные диаграммы для последовательной цепи при согласном (рис.6.2,а) и встречном (рис.6.2,б) включении строятся на основании уравнения (6.2).
В основе другого метода определения взаимной индуктивности лежит использование индуктивно связанных катушек в качестве воздушного трансформатора (рис. 6.1, б) в режиме холостого хода 
Для определения М по схеме, приведенной на схеме (рис.6.1,б) достаточно показаний вольтметра и амперметра, что вытекает из уравнения связи между напряжением на входе второй разомкнутой катушки и током первой:

Взаимная индуктивность вычисляется по модулям действующих значений тока и напряжения:
 . (6.6)
. (6.6)
Если к катушке  подключить сопротивление нагрузки (рис 6.3), то во вторичной цепи появится ток
подключить сопротивление нагрузки (рис 6.3), то во вторичной цепи появится ток  . Так как воздушный трансформатор не содержит ферромагнитного сердечника, являющегося нелинейным элементом, ток
. Так как воздушный трансформатор не содержит ферромагнитного сердечника, являющегося нелинейным элементом, ток  и напряжение на нагрузке
и напряжение на нагрузке  пропорциональны входному напряжению
пропорциональны входному напряжению  Линейность — важнейшее свойство воздушного трансформатора.
Линейность — важнейшее свойство воздушного трансформатора.

Рис.6.3
Уравнения, составленные по законам Кирхгофа для первичной и вторичной цепей трансформатора, записываются в соответствии с выбранными положительными направлениями токов и напряжений:
 (6.7)
(6.7)
На основе уравнений (6.7) может быть построена векторная диаграмма токов и напряжений первичной и вторичной цепей трансформатора. На рис. 6.4 показано построение для случая активно-индуктивной нагрузки. Исходными данными является величина тока во вторичной цепи  а также параметры нагрузки самого трансформатора. Порядок построения следующий: выбираем масштаб токов и напряжений, затем в произвольном направлении строим вектор
а также параметры нагрузки самого трансформатора. Порядок построения следующий: выбираем масштаб токов и напряжений, затем в произвольном направлении строим вектор  . Векторы активных напряжении
. Векторы активных напряжении  и
и  совпадают с
совпадают с  , векторы
, векторы  и
и  опережают
опережают  на 90°. В соответствии с уравнением для вторичной цепи вектор
на 90°. В соответствии с уравнением для вторичной цепи вектор  строим как сумму напряжений вторичной цепи:
строим как сумму напряжений вторичной цепи:

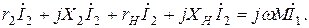
По величине и направлению вектора  определяем величину и направление вектора тока
определяем величину и направление вектора тока  . После построения вектора тока
. После построения вектора тока  строим векторы напряжений первичной цепи.
строим векторы напряжений первичной цепи.

Рис.6.4
Домашнее задание
1. Изучить раздел «Цепи с индуктивно связанными элементами».
2. Определить комплексы тока, напряжений само- и взаимоиндукции катушек, напряжений на их активных сопротивлениях и комплексы полных напряжений обеих катушек (см. рис. 6.1,а). Построить полную векторную диаграмму цепи, указывая напряжения само- и взаимоиндукции обеих катушек.
3. Определить токи  и напряжение на нагрузке
и напряжение на нагрузке  в схеме воздушного трансформатора (см. рис.6.3).
в схеме воздушного трансформатора (см. рис.6.3).
Примечание. Параметры электрических цепей приведены в табл. 6.1.
Таблица 6.1
| № варианта | Соединение катушек | Вх.
напр. 
| Частота

| Параметры катушек | Сопр нaгp. | ||||

| 
| 
| 
| 
| |||||
| В | Гц | Ом | Ом | мГн | мГн | мГн | Ом | ||
| Согласное | 20.5 | ||||||||
| Встречное | 18,5 | ||||||||
| Согласное | 18,3 | 18,9 | 38,5 | 43,4 | |||||
| Встречное | |||||||||
| Встречное | 15,5 | 14,5 | |||||||
| Согласное |
Последовательность выполнения работы
1. Определить индуктивность каждой катушки, считая их активные сопротивления  и
и  , известными из табл. 6.1. Для этого собрать схему в соответствии с рис. 6.5, установить с помощью генератора напряжение заданной частоты на зажимах катушки и измерить ток.
, известными из табл. 6.1. Для этого собрать схему в соответствии с рис. 6.5, установить с помощью генератора напряжение заданной частоты на зажимах катушки и измерить ток.
Результаты измерений позволяют определить полное сопротивление первой катушки:

С другой стороны,
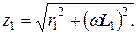
Отсюда

Рис.6.5
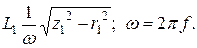
По такой же методике определить индуктивность  второй катушки.
второй катушки.
Найденные значения индуктивностей сравнить с заданными и занести в табл.6.2.
Таблица 6.2
| Первая катушка | Вторая катушка | ||||||

| 
| 
| 
| 
| 
| 
| 
|
| В | мА | Ом | мГн | В | мА | Ом | мГн |
2. Определить взаимную индуктивность М на основе соотношения (6.3) и первой методики, описанной в разделе «Основные теоретические положения». Собрать схему согласно рис.6.1, а. Внутреннюю катушку при этом установить параллельно наружной так, чтобы индуктивная связь была максимальной. Для перехода от согласного включения к встречному (или от встречного к согласному) изменить направление тока в одной из катушек путем переключения проводников на ее зажимах. При вычислении реактивных сопротивлений по формулам (6.4) воспользоваться активными сопротивлениями катушек из табл. 6.1. Результаты измерений и вычислений занести в табл.6.3.
Таблица 6.3
| Тип включения |  ,
В ,
В
|  ,
мА ,
мА
|  ,
Гц ,
Гц
|  ,
ОМ ,
ОМ
| 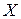 ,
Ом ,
Ом
|  ,
мГн ,
мГн
|  ,
мГн ,
мГн
|
| Согласное | |||||||
| Встречное |
Определить одноименные зажимы катушек. Нарисовать чертеж расположения зажимов и отметить на нем одноименные.
3. Исследовать влияние угла  между плоскостями катушек на взаимную индуктивность и коэффициент связи. Катушки соединить последовательно, подать на них напряжение и частоту те же, что и в предыдущих опытах.
между плоскостями катушек на взаимную индуктивность и коэффициент связи. Катушки соединить последовательно, подать на них напряжение и частоту те же, что и в предыдущих опытах.
Изменяя угол  , произвести измерение тока цепи. Полное сопротивление цепи z, реактивное сопротивление цепи Х и эквивалентную индуктивность цепи L рассчитать, как в п.2. Взаимную индуктивность определить по соотношению
, произвести измерение тока цепи. Полное сопротивление цепи z, реактивное сопротивление цепи Х и эквивалентную индуктивность цепи L рассчитать, как в п.2. Взаимную индуктивность определить по соотношению
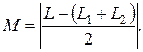
Таблица 6.4
| № П/П | Опытные данные | Расчетные данные | ||||||
 , ,
|  , ,
|  , ,
|  , ,
| 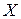 , ,
|  , ,
|  , ,
|  , ,
| |
| град | В | мА | Ом | Ом | мГн | мГн | ||
Значения индуктивностей катушек  и
и  взять из п.1. Коэффициент связи К вычислить по формуле 6.1. Опытные и расчетные данные свести в табл.6.4.
взять из п.1. Коэффициент связи К вычислить по формуле 6.1. Опытные и расчетные данные свести в табл.6.4.
Построить графики зависимостей  , по графику
, по графику  определить области (углы) согласного и встречного включений.
определить области (углы) согласного и встречного включений.
4. Определить взаимную индуктивность М обмоток трансформатора методом холостого хода. Для этого собрать схему (рис. 6.1, б) (плоскости катушек совместить), установить напряжение и частоту согласно п.2. Измерить первичный ток и вторичное напряжение и по соотношению (6.6) определить М. Сравнить с  из п.2.
из п.2.
5. Исследовать трансформатор в нагрузочном режиме. Собрать схему трансформатора с нагрузкой (см. рис.6.3). Для получения максимальной связи внутреннюю катушку установить параллельно наружной. При заданном входном напряжении, частоте и сопротивлении нагрузки (см. табл.6.1) измерить первичный и вторичный токи и напряжение на нагрузке. Сравнить с результатами расчета.
На основании измеренных токов, известных параметров катушек и сопротивлений нагрузки построить векторную диаграмму трансформатора.
Основные вопросы к работе
1. Какие способы применяются для экспериментального определения взаимной индуктивности?
2. Как определить одноименные зажимы индуктивно связанных катушек?
3. Почему при повороте внутренней катушки, включенной последовательно с наружной, изменяется ток в цепи?
4. Как построить векторную диаграмму воздушного трансформатора?
Литература






