а) измерить вольтметром и занести в табл.3.2 в графу «Опыт» напряжения  Пересчитать по закону Ома напряжения
Пересчитать по закону Ома напряжения  ;
;
б) измерить фазометром начальную фазу у тока I. (В качестве «Опорного» взять входное напряжение U, а в качестве «Сигнала» взять напряжение  т.е. клемму «Земля» подключить к общему узлу 4, клемму «Сигнал» - к узлу 3, а клемму «Опорное» - к узлу 1. Обратить внимание, что напряжения
т.е. клемму «Земля» подключить к общему узлу 4, клемму «Сигнал» - к узлу 3, а клемму «Опорное» - к узлу 1. Обратить внимание, что напряжения  и
и  согласованы;
согласованы;
в) прямое измерение начальной фазы  напряжения
напряжения  в цепи на рис. 3.5 невозможно, так как
в цепи на рис. 3.5 невозможно, так как  и
и  не имеют общего узла. Прямое измерение станет возможным, если на время измерения фазы поменять местами резистор
не имеют общего узла. Прямое измерение станет возможным, если на время измерения фазы поменять местами резистор  и С. Тогда фазометр подключается к тем же узлам, что и в пункте “б”. Выполнить это измерение. Результат занести в графу
и С. Тогда фазометр подключается к тем же узлам, что и в пункте “б”. Выполнить это измерение. Результат занести в графу  - прям.;
- прям.;
г) в реальных цепях перемена элементов местами не всегда возможна. По этой причине выполнить измерение начальной фазы  косвенным методом (без перемены местами R и С). Для этой цели зажим «Земля» фазометра подключить к узлу 3, зажим «Сигнал» - к узлу 2, а зажим «Опорное» - к узлу 4. Записать показания
косвенным методом (без перемены местами R и С). Для этой цели зажим «Земля» фазометра подключить к узлу 3, зажим «Сигнал» - к узлу 2, а зажим «Опорное» - к узлу 4. Записать показания  фазометра. Поскольку
фазометра. Поскольку  и
и  не согласованы, то угол
не согласованы, то угол  между
между  определим согласно (3.12), вычитая из показания
определим согласно (3.12), вычитая из показания  угол 180°. Если к результату прибавить измеренную раннее начальную фазу
угол 180°. Если к результату прибавить измеренную раннее начальную фазу  тока (совпадающую с начальной фазой для
тока (совпадающую с начальной фазой для  ), то получим начальную фазу для
), то получим начальную фазу для  т.е.
т.е.  . Результат занести в графу
. Результат занести в графу  – косв. Сопоставить результаты прямого и косвенного измерений
– косв. Сопоставить результаты прямого и косвенного измерений  ;
;
д) начальная фаза  для
для  измеряется непосредственно (зажим «Земля» подключить к узлу 1, зажим «Сигнал» - к узлу 2, зажим «Опорное» - к узлу 4). Напряжения
измеряется непосредственно (зажим «Земля» подключить к узлу 1, зажим «Сигнал» - к узлу 2, зажим «Опорное» - к узлу 4). Напряжения  и
и  согласованы;
согласованы;
е) начальные фазы, измеренные в пп. б, в, г, занести в табл. 3.2 в графу «Опыт».
2. Собрать параллельную цепь на рис. 3.9 с добавочным резистором  и выставить с помощью вольтметра напряжение U=10 B не на входе цепи, а на сопротивлении
и выставить с помощью вольтметра напряжение U=10 B не на входе цепи, а на сопротивлении  . В этом случае комплексные токи параллельных ветвей на рис.3.7 и 3.6 будут одинаковы. Наличие резистора
. В этом случае комплексные токи параллельных ветвей на рис.3.7 и 3.6 будут одинаковы. Наличие резистора  позволяет измерить входной ток
позволяет измерить входной ток  ;
;
а) измерить напряжение на  и пересчитать в ток
и пересчитать в ток  ;
;
б) при измерении фазы  , входного тока в качестве опорного следует взять напряжение
, входного тока в качестве опорного следует взять напряжение  на резисторе
на резисторе  . Тогда клемму «Земля» нужно подключить к общему узлу 2, клемму «Сигнал» – к узлу 1, клемму «Опорное» – к узлу 3.
. Тогда клемму «Земля» нужно подключить к общему узлу 2, клемму «Сигнал» – к узлу 1, клемму «Опорное» – к узлу 3.
Внимание! Напряжения  2 и U не согласованы. Измеренный комплексный ток
2 и U не согласованы. Измеренный комплексный ток  занести в табл.3.3. Токи параллельных ветвей не измеряются.
занести в табл.3.3. Токи параллельных ветвей не измеряются.
3. Собрать разветвленную цепь согласно варианту (рис.3.10 – 3.12). Подключить к цепи генератор заданной частоты с напряжением U =10 В:
а) измерить вольтметром напряжения на резисторах  и напряжения
и напряжения  Пересчитать напряжения резисторов в токи
Пересчитать напряжения резисторов в токи 
б) измерить фазометром начальные фазы токов  Занести в табл.3.4 в графу «Опыт» комплексные токи
Занести в табл.3.4 в графу «Опыт» комплексные токи  и модули напряжений
и модули напряжений 
4.Сделать заключение о соответствии расчетных и опытных данных по всем выполненным пунктам работы.
Основные вопросы к работе
1.Основные величины, характеризующие синусоидальный ток и напряжение (период, частота, угловая частота, начальная фаза, амплитуда, действующее значение).
2.С какой целью введено понятие действующего значения гармонического сигнала? Может быть, достаточно понятия амплитуды сигнала?
3.Какой смысл содержится в понятии положительного направления синусоидального напряжения и тока?
4.Что такое комплексный ток, напряжение? Что понимают под комплексной амплитудой тока, напряжения?
5.Как вычисляются комплексные сопротивления элементов цепи?
6.Каковы фазовые сдвиги между напряжениеми током в индуктивности, емкости?
7.Для какого класса цепей (R -цепи, RL -цепи, RC -цепи, LC -цепи, RLC -цепи) угол  сдвига фаз между входными напряжением и током может равняться: а) нулю, б) ±90°?
сдвига фаз между входными напряжением и током может равняться: а) нулю, б) ±90°?
8. Что характеризуют активная, реактивная и полная мощности? Единицы их измерения.
9.Что такое коэффициент мощности?
10.На каком важном свойстве линейных цепей основан метод пропорционального пересчета?
11.Как строится топографическая диаграмманапряжений цепи?В чем ееотличие от векторной диаграммы напряжений?
12. Опишите особенности использования фазометра.
Лабораторная работа №3Б
ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Цель работы
Определение параметров простейших эквивалентных схем замещения двухполюсника. Экспериментальная проверка законов распределения тока и напряжения в линейной разветвленной цепи гармонического тока, проверка балансов активных и реактивных мощностей, приобретение навыков работы с вольтметром, фазометром и генератором.
Основные теоретические положения
Лабораторная работа №3Б является углубленным вариантом предыдущей работы №3А. Поскольку ниже изложены только дополнительные теоретические сведения, следует предварительно ознакомиться с теоретическим материалом к работе №3А.
Рассмотрим схему включения фазометра и расчетные формулы для экспериментального определения параметров схемы замещения таких реальных элементов, как катушка индуктивности и конденсатор (рис. 3.13).

Рис.3.13
1. Катушка индуктивности. Если катушку индуктивности представить последовательной схемой замещения, то цепь на рис.3.14, а и соответствующая ей векторная диаграмма напряжений примут вид, приведенный на рис. 3.14, б.
Обратим внимание, что напряжение сигнала  и опорное напряжение
и опорное напряжение  на рис.3.14,а не согласованы, поэтому угол а сдвиги фаз между ними (рис.3.14, б) вычисляется согласно формуле (3.12) в работе №3А путем добавления к показанию
на рис.3.14,а не согласованы, поэтому угол а сдвиги фаз между ними (рис.3.14, б) вычисляется согласно формуле (3.12) в работе №3А путем добавления к показанию  фазометра угла ±180°.
фазометра угла ±180°.
Из рис. 3.14, б находим


Рис.3.14
Учитывая, что

для параметров последовательной схемы замещения катушки получим

 (3.13)
(3.13)
Для параллельной схемы замещения индуктивной катушки цепь на рис. 3.13 и векторная диаграмма примут вид, показанный на рис. 3.15.

Рис.3.15
Из рис. 3.15, а следует:

Поскольку из диаграммы на рис. 3.15, б видно, что


то для проводимостей параллельной схемы замещения катушки получим формулы
 (3.14)
(3.14)
Формулы (3.14) можно получить и без анализа векторной диаграммы, если подставить выражения (3.13) в переходные формулы (3.6) из работы №ЗА.
2. Конденсатор. Методика вывода формул для параметров схем замещения конденсатора такая же, как и для катушки. Поэтому приведем только окончательные формулы.
 Рис.3.16
Рис.3.16
|
Для последовательной схемы замещения рис.3.16, а
 (3.15)
(3.15)
 (3.16)
(3.16)
Для параллельной схемы замещения рис.3.16, б
 (3.17)
(3.17)
 (3.18)
(3.18)
В радиотехнике и электросвязи качество реальных катушек и конденсаторов оценивают с помощью их добротности Q на заданной частоте, которая характеризует степень приближения катушки к идеальной индуктивности и конденсатора – к идеальной емкости.
Добротность катушки
 (3.19)
(3.19)
Добротность конденсатора
 (3.20)
(3.20)
В формулах (3.19), (3.20) α – угол фазового сдвига между напряжением и током катушки и конденсатора (см. рис. 3.14,б). На практике добротность элементов измеряют с помощью специальных измерительных приборов – Q - метров, а формулы (3,19), (3,20) используют для расчета сопротивления потерь  Отметим, что при использовании реальных элементов на фиксированной частоте в равной мере могут применяться как последовательная, так и параллельная схемы замещения катушки и конденсатора. Если же эксплуатация элементов осуществляется в некотором диапазоне частот, то для катушки предпочтительнее последовательная схема замещения, а для конденсатора - параллельная. Отмеченный приоритет схем замещения обусловлен тем, что параметры этих схем слабее зависят от частоты.
Отметим, что при использовании реальных элементов на фиксированной частоте в равной мере могут применяться как последовательная, так и параллельная схемы замещения катушки и конденсатора. Если же эксплуатация элементов осуществляется в некотором диапазоне частот, то для катушки предпочтительнее последовательная схема замещения, а для конденсатора - параллельная. Отмеченный приоритет схем замещения обусловлен тем, что параметры этих схем слабее зависят от частоты.
Описание лабораторной установки
Используемые в настоящей работе приборы (перестраиваемый генератор синусоидального напряжения, вольтметр, фазометр) и лабораторный макет такие же, как и в лабораторной работе №3А. Поэтому следует внимательно ознакомиться с описанием установки в работе №3А.
Особое внимание обратить на особенности использования фазометра. В табл. 3.5 заданы для шести вариантов параметры генератора  и номиналы элементов. Величины
и номиналы элементов. Величины  и
и  являются резистивным сопротивлением и индуктивностью последовательной схемы замещения катушки. При расчете домашнего задания конденсатор замещается идеальной емкостью С.
являются резистивным сопротивлением и индуктивностью последовательной схемы замещения катушки. При расчете домашнего задания конденсатор замещается идеальной емкостью С.
Таблица 3.5
| Вариант | Схема на рис. |  ,
В ,
В
|  ,
Гн ,
Гн
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
мГн ,
мГн
|  ,
Ом ,
Ом
|  ,
мкФ ,
мкФ
|
| 3.17 | 0.93 | ||||||||
| 3.17 | 0.93 | ||||||||
| 3.18 | 0.95 | ||||||||
| 3.18 | 42.5 | 0.99 | |||||||
| 3.19 | 0.96 | ||||||||
| 3.19 | 1.0 |
Домашнее задание
Домашнее задание выполняется каждым студентом и включает следующие пункты:
1. Для последовательной цепи на рис. 3.5 (работа №3А):
а) рассчитать согласно варианту сопротивления  реактивных элементов комплексное входное сопротивление цепи, комплексный ток
реактивных элементов комплексное входное сопротивление цепи, комплексный ток  и комплексные напряжения элементов
и комплексные напряжения элементов  Параметры цепи и генератора заданы в табл.3.5. Потерями в конденсаторе пренебречь. Начальную фазу напряжения генератора принять равной нулю. Все расчетные величины занести в графу «расчет» табл. 3.6;
Параметры цепи и генератора заданы в табл.3.5. Потерями в конденсаторе пренебречь. Начальную фазу напряжения генератора принять равной нулю. Все расчетные величины занести в графу «расчет» табл. 3.6;
б) по результатам расчетов построить топографическую диаграмму напряжений всех элементов цепи.
Таблица 3.6
| Цепь на рис. 3.5 | 
| 
| 
| 
| 
| 
| 
| ||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||||
| прям. | косв. | ||||||||||||
| Ом | Ом | Ом | град | мА | град | В | град | В | град | град | В | град | |
| Расч. | |||||||||||||
| Опыт | — | — |
2. Рассчитать на заданной частоте добротность  катушки (3.19) и проводимости
катушки (3.19) и проводимости  параллельной схемы замещения катушки (работа №3А, формула 3.6). Результаты занести в табл. 3.7.
параллельной схемы замещения катушки (работа №3А, формула 3.6). Результаты занести в табл. 3.7.
3. Для заданной в табл. 3.5 цепи (рис.3.17 - 3.19) рассчитать двумя методами (первый студент бригады — методом эквивалентных преобразований, второй студент бригады – методом пропорционального пересчета) комплексные токи 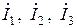 всех ветвей цепи, а также комплексные напряжения
всех ветвей цепи, а также комплексные напряжения  последовательной и
последовательной и  параллельных ветвей цепи (начальную фазу питающего напряжения принять равной нулю).
параллельных ветвей цепи (начальную фазу питающего напряжения принять равной нулю).

Рис.3.17 Рис.3.18
4. По расчетным данным п. 3 построить в единой системе координат векторную диаграмму токов и топографическую диаграмму напряжений. Масштабы  и
и  взять достаточно крупными и разными.
взять достаточно крупными и разными.

Рис.3.19 Рис.3.20
Таблица 3.7
| Расчет | ||||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 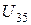
| 
| 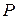
| 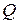
|
| См | См | мА | град | мА | град | мА | град | В | град | В | град | Вт | вар | |
Таблица 3.8
| Опыт | |||||||||||||||
| Катушка индуктивности | Конденсатор | ||||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| В | В | град | град | мГн | Ом | См | См | В | В | град | град | мкФ | Ом | ||
Таблица 3.9
| Опыт | |||||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 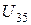
| 
| 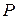
| 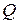
| |
| В | мА | град | В | мА | град | В | мА | град | В | град | В | град | Вт | вар | |
5. Вычислить активные и реактивные мощности источника и потребителей. Проверить баланс активных и реактивных мощностей.






