Краткая теория исследуемого явления. Рассчитать магнитное поле – это значит найти в каждой точке пространства величину и направление вектора магнитной индукции (или напряженности )

Рассчитать магнитное поле – это значит найти в каждой точке пространства величину и направление вектора магнитной индукции 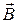(или напряженности ). Определение векторов 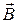и см. в лабораторной работе № 32.

Расчет магнитных полей необходим при конструировании электромагнитов, генераторов переменного тока, трансформаторов, электродвигателей, ускорителей элементарных частиц и т.д.

Для определения вектора магнитной индукции используют закон Био-Савара-Лапласа и принцип суперпозиции полей. Закон Био-Савара-Лапласа для проводника с током I, элемент которого dl создает в некоторой точке индукцию поля , записывается в виде

, (1)

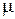где – радиус-вектор, проведенный от элемента проводника в точку наблюдения, – магнитная проницаемость вещества, Гн/м – магнитная постоянная.

Направление вектора определяется векторным произведением или правилом правого винта. Модуль вектора определяется выражением

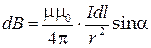, (2)

где 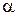– угол между направлением тока и вектором .

Результирующее поле, создаваемое проводником произвольной формы или несколькими проводниками, определяется согласно принципу суперпозиции

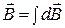или . (3)

Для создания магнитного поля с необходимым значением индукции используют соленоиды.

Соленоидом называют цилиндрическую катушку, состоящую из большого числа витков N проволоки, образующих винтовую линию. Если витки расположены достаточно близко друг к другу, соленоид представляет собой систему последовательно соединенных круговых токов одинакового радиуса, имеющих общую ось (рис.1).

Рис. 1

Линии магнитной индукции 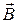(напряженности ) замкнутые. На рис. 2 показана конфигурация магнитного поля соленоида.

Рис. 2

Применяя закон Био-Савара-Лапласа и принцип суперпозиции полей, можно получить выражение для индукции магнитного поля В в произвольной точке А на оси соленоида (рис.1)

. (4)

Учитывая, что , получим

, (5)

где – количество витков соленоида, приходящееся на 1 м длины.

Характер поля соленоида зависит от соотношения его длины l и радиуса R. При l>> 2 R соленоид называют бесконечно длинным. В этом случае магнитное поле сосредоточено внутри соленоида, оно однородно ; вне соленоида поле практически отсутствует.

Магнитное поле внутри конечного соленоида неоднородно, величина В убывает от его середины к концам. В середине такого соленоида В несколько меньше, чем у бесконечного соленоида с тем же количеством витков на единицу длины n. Вне соленоида .

Выражая и в формуле (5) через размеры соленоида можно получить для напряженности Н магнитного поля в центре соленоида

(6)

и для на краю соленоида (при или )

. (7)

При расчете полей, создаваемых большим количеством токов, используют обобщение закона Био-Савара-Лапласа – закон полного тока (теорему о циркуляции вектора 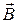): циркуляция вектора 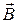по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:

. (8)

Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему. Выражение (8) справедливо для поля в вакууме.

Выбрав произвольный контур охватывающий витки бесконечно длинного соленоида АDСBА, так, чтобы интеграл выражения (8) вычислялся наиболее просто:

,

получим для индукции магнитного поля

. (9)

Полагая в выражении (6) R<<l, получим для В в центре конечного соленоида 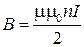, что в два раза меньше В в бесконечно длинном соленоиде. В соленоиде без сердечника .