МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по курсу "Информатика"
по теме:
"Арифметические основы ЭВМ "
Ростов-на-Дону
Составитель: Красников В.В.
Методические указания к практическим занятиям по курсу "Информатика" по теме "Арифметические основы ЭВМ". Ростов н/Д: ДГТУ, 2004 – 22 с.
Методические указания предназначены для проведения практических занятий по курсу "Информатика" у студентов специальностей 071900 и 351400, а также для студентов других специальностей, в той или иной степени знакомящихся с организацией ЭВМ. В методических указаниях рассмотрены принципы построения позиционных систем счисления, правила перевода чисел из одной системы счисления в другую, двоичная арифметика, а также основные принципы хранения и обработки числовой информации в ЭВМ. Методические указания содержат большое число примеров и заданий.
Печатается по решению методической комиссии факультета "Автоматизация и информатика"
Рецензент: к.ф.-м.н. Бычков А.А.
© ДГТУ
1. Системы счисления.
Основные понятия и определения.
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
Все системы счисления делятся на позиционные и непозиционные.
Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе.
Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону.
Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество  различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления - “
различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления - “  ”.
”.
В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.
Любое число N в позиционной системе счисления с основанием  может быть представлено в виде полинома от основания
может быть представлено в виде полинома от основания  :
:
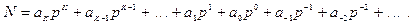 (1.1)
(1.1)
здесь 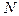 - число,
- число,  - коэффициенты (цифры числа),
- коэффициенты (цифры числа),  - основание системы счисления (
- основание системы счисления ( >1).
>1).
Принято представлять числа в виде последовательности цифр:
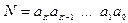 .
. 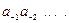
В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Точка опускается, если нет отрицательных степеней (число целое).
В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое - 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.
Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде:
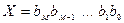 .
. 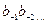 ,
,
где 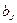 либо 0, либо 1.
либо 0, либо 1.
Эта запись соответствует сумме степеней числа 2, взятых с указанными коэффициентами:
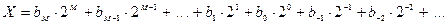
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таб. 1).
Таб. 1. Наиболее важные системы счисления.
|
Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр – латинскими буквами: 10–A, 11–B, 12–C, 13–D, 14–E, 15–F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таб. 1).
Перевод чисел из одной системы счисления в другую.
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.






