На рис.5.2 приведена векторная диаграмма напряжений и токов для симметричной нагрузки, соединённой треугольником.
Рис.5.2
Из диаграммы видно: 
, где 
;
. Таким образом, при соединении треугольником соотношение между линейными и фазными токами выражается формулой: 
.
Если нагрузка несимметрична, то 
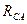. Тогда, можно построить векторную диаграмму напряжений и токов, представленную на рис.5.3.
Рис.5.3
При обрыве фазы ab рассмотрим схему, изображённую на рис.5.4.
Рис.5.4
Тогда вектор тока 
, и можно записать следующие выражения: 
, 
, 
. На основании этих выражений, можно построить векторную диаграмму напряжений и токов, приведённую на рис.5.5.
Рис.5.5
При обрыве фаз ab и bc векторы токов и 
, тогда схема будет иметь вид, показанный на рис.5.6.
Рис.5.6
При этом выражения для линейных и фазных токов преобразуются в следующий вид: , 
, 
.
На рис.5.7 приведена векторная диаграмма напряжений и токов при обрыве фаз ab и bc нагрузки, соединённой треугольником.
Рис.5.7
Рассмотрим схему обрыва линейного провода, изображённую на рис.5.8. Пусть 
. При обрыве линейного провода Аa вектор линейного тока 
. Преобразуем схему рис.5.8 в схему рис.5.9.
Рис.5.8
Рис.5.9
Из преобразованной схемы следует: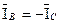 
, 
, 
.
По первому закону Кирхгофа:
; 
.
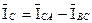Используя выше приведённые формулы, построим векторную диаграмму, приведённую на рис.5.10.
Рис.5.10
При симметричной нагрузке активная мощность трёхфазной цепи равна сумме активных мощностей фаз: P = 
. Активную мощность трёхфазной цепи можно выразить через фазные значения напряжения и тока:
P = 
.
При соединении звездой соотношения между фазными и линейными напряжениями и токами равны: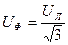 
, 
. При соединении треугольником эти соотношения равны: 
= 
, 
. В обоих случаях 
. Тогда активную мощность можно выразить через линейные значения напряжения и тока:
P = 
.
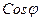
Реактивная мощность трёхфазной цепи:
Q = 
= 
.
Полная мощность трёхфазной цепи:
S =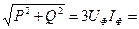 
.
При расчётах удобно пользоваться следующими формулами:
; 
; 
= 
; = 
; 
= 
.
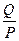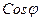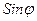4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
4.1. Ознакомиться с оборудованием и приборами, необходимыми для выполнения работы, и записать их основные технические данные.
4.2. Собрать трёхфазный симметричный потребитель, соединенный по схеме «треугольник» (рис. 5.11).
Рис.5.11
4.3. Собранную схему представить для проверки преподавателю или лаборанту, с их разрешения приступить к работе. Тумблер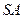 
замкнуть.
При симметричной нагрузке включить по четыре лампы в каждой фазе, подать питание на схему. Снять показания приборов и занести их в табл. 5.1. Сравнить эти данные с теоретическими соотношениями между напряжениями, линейными и фазными токами.
Таблица 5.1
А) Измерено:
| Нагрузка | 
| 
| 
| 
| 
| 
| 
| 
| 
|
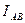
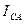
| Симметричная (по 4 лампы в фазе) | |||||||||
| Несимметричная (по 2,3,4 лампы в фазе) | |||||||||
| Обрыв фазы bc (по 4 лампы в фазе) | |||||||||
| Обрыв линейного провода (по3 лампы в фазе) |
Б) Вычислено:
| Нагрузка |  
| 
|  
| 
|
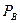
| Симметричная (по 4 лампы в фазе) | ||||
| Несимметричная (по 2,3,4 лампы в фазе) | ||||
| Обрыв фазы bc (по 4 лампы в фазе) | ||||
| Обрыв линейного провода (по3 лампы в фазе) |
4.4. При включенном тумблере 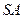и несимметричной нагрузке, включить в каждой фазе лампового реостата различное число ламп по две, три, четыре в каждой фазе. Снять показания приборов и занести их в табл. 5.1.
4.5. При включенном тумблере 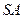произвести обрыв фазы bc, отключив в ней все лампы, в других фазах включить по 4 лампы. Снять показания приборов и занести их в табл. 5.1.
4.6. Разомкнуть тумблер 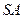(обрыв линейного провода). Включить в каждой фазе по 3 лампы. Снять показания приборов и записать их в табл. 5.1.
4.7. Результаты измерений предъявить для проверки преподавателю и с его разрешения разобрать схему.
5. СОДЕРЖАНИЕ ОТЧЕТА
5.1. Номер, наименование и цель работы.
5.2. Перечень электрооборудования и приборов с указанием их технических данных.
5.3. Принципиальная электрическая схема испытаний (рис.5.11).
5.4.Таблица с результатами измерений и вычислений.
5.5. Векторные диаграммы напряжений и токов по результатам измерений при различных нагрузках с указанием масштабов.
5.6. Результаты сравнений экспериментальных и теоретических соотношений между напряжениями и токами. Здесь необходимо показать, что при симметричной нагрузке фаз справедливо равенство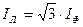 
.
5.7. Результаты вычисления мощности.
5.8. Краткие выводы по работе, где отразить следующие вопросы:
подтверждение теории на опытных данных эксперимента;
влияние несимметричной нагрузки на величину фазных токов и работу потребителя;
достоинства и недостатки соединения потребителей «треугольником»;
где и по каким причинам соединение «треугольником» нашло наибольшее распространение.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. В трёхфазную линию включены приёмники по схеме «треугольник». Изобразите соответствующую схему и введите в неё измерительные приборы для измерения линейных и фазных токов и напряжений.
6.2. Какой режим работы трёхфазного приёмника, соединённого «треугольником», называется симметричным?
6.3. Какой режим работы трёхфазного приёмника, соединённого «треугольником», называется несимметричным?
6.4. Приведите основные свойства симметричной трёхфазной системы синусоидальных ЭДС.
6.5. Напишите выражения мгновенных значений напряжений, образующих трёхфазную симметричную систему (для фазы “А” принять начальную фазу напряжения, равную нулю).
6.6. Напишите выражения мгновенных значений токов, образующих симметричную трёхфазную систему, если начальная фаза тока в фазе “А” равна 
.
6.7. Расскажите порядок построения векторной диаграммы для симметричной активной нагрузки фаз, соединённых “ треугольником ”.
6.8. Расскажите порядок построения векторной диаграммы для симметричной активно-индуктивной нагрузки фаз, соединённых “треугольником”.
6.9. Расскажите порядок построения векторной диаграммы для симметричной активно-емкостной нагрузки фаз, соединённых “ треугольником ”.
6.10. Почему в соединении “треугольник” токи в линейных проводах определяется геометрическим суммированием токов фаз, а не алгебраическим?
6.11. Расскажите порядок построения векторной диаграммы для несимметричной активной нагрузки фаз, соединённых “ треугольником ”.
6.12. Расскажите порядок построения векторной диаграммы для несимметричной активной нагрузки фаз, соединённых “ треугольником ”.
6.13. Докажите, что в симметричной трёхфазной системе, соединённой по схеме “треугольник”, геометрическая сумма линейных токов всегда равна нулю.
6.14. Как производится расчёт системы “треугольник” при симметричной нагрузке фаз?
6.15. Напишите выражения активной, индуктивной и полной мощностей трёхфазной системы, соединённой по схеме “треугольник” при симметричном режиме работы.
6.16. Расскажите порядок построения векторной диаграммы для соединения “треугольник” при обрыве одной из фаз.
6.17. Расскажите порядок построения векторной диаграммы для соединения “треугольник” при обрыве двух фаз.
6.18. Напишите соотношения между линейными и фазными напряжениями и токами при симметричной нагрузке в соединении “треугольником”.
6.19. Как определяются линейные токи в системе “треугольник” при несимметричном режиме работы фаз?
7. ВОПРОСЫ К ЗАЩИТЕ
7.1. Построить векторные диаграммы при замкнутом и разомкнутом ключе “S” (см. рис.5.12).
7.2. Как изменится векторная диаграмма при переводе ключа “S” из положения 1 в положение 2 (см. рис.5.13).
7.3. Построить векторную диаграмму для цепи, представленной на рис.5.14.
7.4. Определить показания приборов после размыкания рубильника “ S ” (см. рис.5.15), если 
.
7.5. Построить векторную диаграмму для цепи, представленной на рис.5.16.
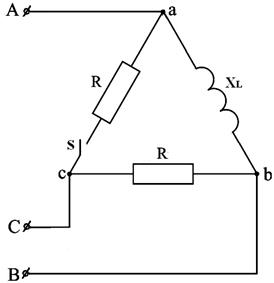
Рис.5.12
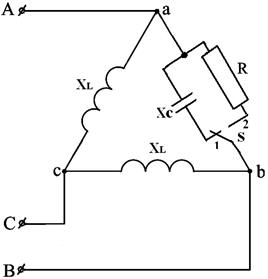
Рис.5.13
Рис.5.14
7.6. Определить показания приборов (см. рис.5.17) для опытов, когда 
:
а) все ключи замкнуты;
б) замкнуты ключи 
а ключ 
- разомкнут;
в) замкнуты ключи 
а ключ 
- разомкнут.
Рис.5.15 Рис.5.16
7.7. Построить векторную диаграмму для цепи, представленной на рис.5.18.
7.8. Как изменится векторная диаграмма при переводе ключа “ S ” из положения 1 в положение 2 для цепи, представленной на рис.5.19.
7.9. Построить векторные диаграммы при замкнутом и разомкнутом ключе “ S ” (см. рис.5.20).
7.10. Построить векторные диаграммы при замкнутом и разомкнутом ключе “ S ” (см. рис.5.21).
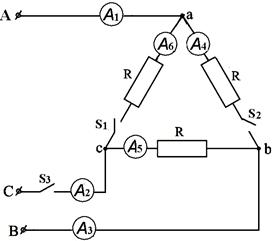
Рис,5.17 Рис.5.18
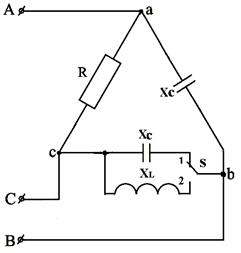
Рис.5.19 Рис.5.20
Рис.5.21
7.11. Построить векторные диаграммы при замкнутом и разомкнутом ключе 
(см. рис. 5.22).
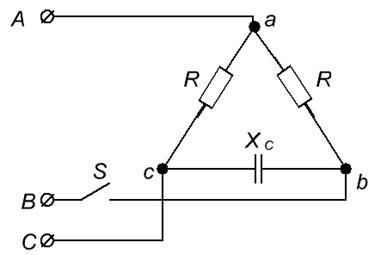
Рис.5.22
7.12. Построить векторную диаграмму для цепи, представленной на рис.5.23.
Рис. 5.23
7.13. Построить векторные диаграммы при замкнутом и разомкнутом ключе (см. рис. 5.24).
Рис. 5.24
7.14. Построить векторные диаграммы при замкнутом и разомкнутом ключе (см. рис. 5.25).
Рис. 5.25
7.15. Построить векторные диаграммы (рис. 5.26), если:
а) все ключи замкнуты;
б) - разомкнут, 
и - замкнуты;
в) - разомкнут, и - замкнуты;
г) - разомкнут, и - замкнуты.
Рис. 5.26
7.16. Построить векторную диаграмму для цепи, представленной на рис. 5.27.
Рис. 5.27
7.17. Определить показания приборов после размыкания рубильника (см. рис. 5.28), если 
.
Рис. 5.28
7.18. Построить векторную диаграмму для цепи, представленной на рис. 5.29.
Рис. 5.29.
7.19. Определить показания приборов при размыкании рубильника (см. рис. 5.30), если 
.
Рис.5.30
