ББК 31.2 3 страница

Рис.3.2

Из векторной диаграммы находим общий ток:

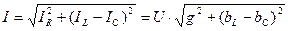, где - полная проводимость цепи.

Откуда 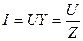, где - полное сопротивление цепи.

Из векторной диаграммы следует, что наличие ёмкости снизило ток I1 до величины I, а cosφ при этом увеличился. Резонанс токов можно практически получить изменением ёмкости конденсатора. На рис. 3.3 приведены примерные графические зависимости IL, IC, I, cosφ от изменения C, где Cp - резонансная ёмкость.

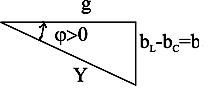
Рис.3.3 Рис.3.4

Выражение соответствует треугольнику проводимостей, представленному на рис. 3.4, откуда следует:

; .

Выражения для мощностей принимают следующий вид:

- активная мощность, - реактивная мощность,

- полная мощность.

При этом треугольник мощностей, показан на рис.3.5, из которого можно определить активную мощность 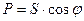, реактивную мощность и полную мощность .

Рис.3.5

Резонансом токов для рассматриваемой цепи называют явление, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением источника. При резонансе токов = 0; cos = 1; bL = bC; I = IR. Пусть резонансная частота f0 определяется из соотношения , тогда , а угловая резонансная частота .

Итак, признаками резонанса токов являются:

а) индуктивная и емкостная проводимости равны;

б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и имеет минимальное значение;

в) коэффициент мощности максимален.

 

4.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

4.1.Ознакомиться с оборудованием и приборами, необходимыми для выполнения работы, и записать их основные технические данные.

4.2.Собрать схему (рис 3.6) и предъявить ее для проверки преподавателю или лаборанту.

Рис.3.6

4.3. Набрать на магазине емкостей C=10мкФ и не выключать эту ёмкость в процессе выполнения работы.

4.4. Включить выключатель сети S. С помощью ЛАТРа установить напряжение питания равным 50В.

4.5. Постепенно изменяя ёмкость контура от 10 мкФ и выше через 1 мкФ, снять 3-4 точки до резонанса токов. С помощью подборки емкостей добиться минимального тока в цепи (резонанс токов).

Показания приборов записать в таблицу 3.1. После резонанса, увеличивая ёмкость до 18 мкФ, сделать еще 4-5 отсчетов.

4.6. Считая активную проводимость цепи с конденсатором равной нулю, для каждого опыта произвести вычисления по ниже приведённым формулам и данные измерений и вычислений записать в таблицу 3.1:

 

Таблица 3.1

№№ опытов	Измерено
U,B	C, мкФ	I, A	IC , A	I k , A	P, Bт

 

 

Вычислено
№№ опытов	bC, сим	bL, сим	g, сим	y, сим	IR, A	IL, A	φ, град	Cos φ	Q, Вар	S, ВА

 

 

4.7.Формулы для вычисления:

Емкостная проводимость - , где C,Ф.; 1мкФ = .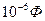

Индуктивная проводимость - 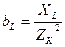, где .

 

Активная проводимость - .

Полная проводимость всей цепи - .

Активная составляющая тока в цепи катушки индуктивности - .

Реактивная составляющая тока всей цепи 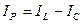, где индуктивная составляющая тока в цепи катушки индуктивности , - заданный емкостной ток.

Угол сдвига фаз . Коэффициент мощности - cos φ = = .

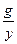Частота собственных колебаний контура - .

Реактивная мощность - , где .

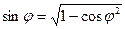Полная мощность .

4.8. По заданию преподавателя построить в выбранном масштабе векторные диаграммы токов для трех случаев:

преобладание в цепи индуктивной проводимости b_L > b_C, I_L > I _C;

преобладание в цепи емкостной проводимости b_L < b_C, I_L < I _C;

резонанс токов b_L = b_C, I_L = I _C.

Построить соответствующие векторным диаграммам токов треугольники проводимостей.

4.9. По данным табл. 3.1 построить в масштабе графики зависимостей: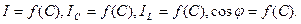

Примерный график изменения токов в цепи показан на рис. 3.7. Момент наступления резонанса токов отметить вертикальной пунктирной линией.

Рис.3.7

4.10. Данные всех измерений предъявить для проверки преподавателю и с его разрешения схему разобрать. Получить задание по п. 4.8.

4.11. Привести в порядок рабочее место.

 

5. СОДЕРЖАНИЕ ОТЧЕТА

5.1. Номер, наименование и цель работы.

5.2. Основные технические данные измерительных приборов и потребителей.

5.3. Принципиальная электрическая схема (рис. 3.6).

5.4. Таблица наблюдений и вычислений; формулы, по которым велись вычисления.

5.5. Векторные диаграммы токов и треугольники проводимостей (п.4.8).

5.6. Кривые зависимостей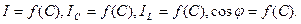

5.7. Краткие выводы по работе, в которых дать ответы на следующие вопросы:

а) как изменяются параметры цепи при изменении емкости?

б) объяснить, почему повышается коэффициент мощности цепи при подключении конденсаторов?

в) какими способами можно получить резонанс токов?

 

6. КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1. Как выражается закон Ома для цепей переменного тока с параллельным соединением

6.2. Почему резонанс в параллельной цепи с элементами называется резонансом токов?

6.3. Если потребитель в цепи переменного тока состоит из параллельно включенных катушки индуктивности и конденсатора, то, какое влияние на оказывает конденсатор?

6.4. Какими способами можно повысить коэффициент мощности?

6.5. По каким формулам определяются активная, реактивная и полная мощности переменного тока.

6.6. Как определить опытным путём резонансную ёмкость?

6.7. Как перейти графически от синусоидальной кривой к векторной диаграмме и наоборот?

6.8. Найдите графически сумму двух периодических синусоидальных токов одинаковой частоты. Определите действующее значение и начальную фазу суммарного тока.

6.9. Построить векторную диаграмму суммы трёх токов.

6.10. Какой из приведённых графиков (см. рис. 3.8) характеризует цепь переменного тока, в которую включено только одно активное сопротивление? Приведите векторную диаграмму такой цепи.

Рис.3.8

6.11. Какой из приведённых графиков (рис. 3.8) характеризует цепь переменного тока, в которую включена:

а) только индуктивность?

б) только ёмкость?

Приведите векторные диаграммы таких цепей.

6.12. Почему при параллельном соединении ток в неразветвлённой части схемы равен геометрической сумме токов в отдельных ветвях, а не алгебраической?

6.13. Как выражается закон Ома для цепей переменного тока с параллельным соединением .

6.14. Приведите векторные диаграммы для цепей переменного тока, имеющих:

а) индуктивный характер?

б) емкостной характер?

6.15. Приведите графики мгновенных значений токов и напряжений для цепей переменного тока, имеющих:

а) индуктивный характер?

б) емкостной характер?

6.16. Начертите треугольники токов, проводимостей и мощностей для цепи переменного тока с активно-индуктивной нагрузкой.

6.17. Начертите треугольники токов, проводимостей и мощностей цепи переменного тока с активно-емкостной нагрузкой.

6.18. Как зависит индуктивная проводимость от частоты? Приведите график этой зависимости.

6.19. Как зависит емкостная проводимость от частоты? Приведите график этой зависимости.

 

7. ВОПРОСЫ К ЗАЩИТЕ

7.1. Амперметры и показывают соответственно: 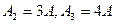. Что покажет амперметр ? Как определить угол фазового сдвига между током и напряжением (рис.3.9)?

Рис. 3.9

7.2. Вычертить электрическую цепь с элементами, включенными параллельно, по приведенной векторной диаграмме (см. рис. 3.10).

 

Рис. 3.10

7.3. Дано: 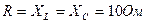. Определить активную, реактивную и полную проводимости цепи (см. рис. 3.11).

Рис. 3.11

 

7.4. Каким схемам с параллельным соединением элементов соответствуют векторные диаграммы, приведенные на рис. 3.12.

Рис. 3.12

 

7.5. Построить векторную диаграмму, соответствующую цепи, приведенной на рис. 3.13, если .

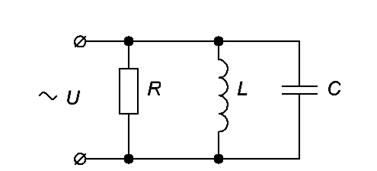
Рис. 3.13

 

7.6. Записать выражение для закона Ома в цепи, приведенной на рис. 3.14.

Рис. 3.14

7.7. Построить векторную диаграмму, соответствующую цепи, изображенной на рис. 3.15.

Рис. 3.15

7.8. При перемещении ключа "К" в "1"положение в цепи (см. рис. 13.16) наблюдается резонанс токов. Известно, что , сохранится ли он при перемещении ключа "К" в положение "2"?

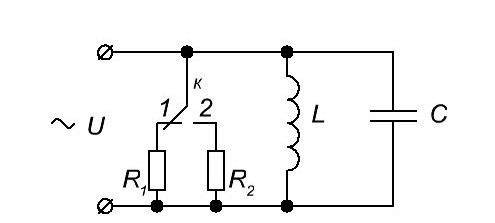
Рис. 3.16

7.9. В цепи (см. рис. 3.17) при частоте . Как изменится векторная диаграмма, при ?

Рис. 3.17

7.10. Определить полную проводимость цепи, если (см. рис.3.18).

Рис. 3.18

7.11. Запишите условие получения резонанса в цепи, представленной на рис. 3.19.

Рис. 3.19

 

7.12. Показания приборов равны: . Найти показание (см. рис.3.20).

Рис. 3.20

7.13. Для цепи, изображенной на рис.3.21, известно: , действующее значение напряжения равно . Как определить активную и реактивную мощности цепи?

Рис. 3.21

7.14. В цепи (см. рис.3.22) известно, что . Определить токи: .

Рис. 3.22

7.15. Каким схемам с параллельным соединением элементов соответствуют векторные диаграммы, приведенные на рис. 3.23.

Рис. 3.23

7.16. В цепи (см. рис. 3.24) известно, что . Найти угол сдвига по фазе между значениями и .

Рис. 3.24

7.17. Записать выражение для закона Ома в цепи, представленной на рис. 3.25.

Рис. 3.25

7.18. Показания приборов . Что покажет амперметр ? Чему равны сопротивления , если (см. рис. 3.26).

Рис. 3.26

7.19. Для цепи, представленной на рис. 3.24, известно, что . Как взаимно расположены вектор тока 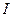и приложенного напряжения ?

 

2.4. ЛАБОРАТОРНАЯ РАБОТА №4

«ИССЛЕДОВАНИЕ ТРЁХФАЗНОЙ СИСТЕМЫ ПРИ СОЕДИНЕНИИ ПОТРЕБИТЕЛЕЙ «ЗВЕЗДОЙ»»

 

1. ЦЕЛЬ РАБОТЫ

Практическое подтверждение теоретических соотношений между линейными и фазными напряжениями и токами при соединении потребителей «звездой».

 

2. ЭЛЕКТРООБОРУДОВАНИЕ И ПРИБОРЫ

2.1. Источник питания трехфазного переменного тока с напряжением (клеммы ).

2.2. Потребители – ламповые реостаты.

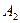2.3. Амперметры и электромагнитной системы типа на ток .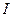

2.4. Амперметры и электромагнитной системы типа на ток .

2.5. Вольтметр электромагнитной системы типа на напряжение .

2.6. Вольтметр электромагнитной системы типа на напряжение .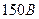

2.7. Вольтметр (переносной) электромагнитной системы типа на напряжение .

2.8. Переключатели (тумблеры) и .

2.9. Соединительные провода.

 

3. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

3.1. Наличие нулевого провода.

Пусть трёхфазная система представлена в виде трёхфазного генератора и активной трёхфазной нагрузки 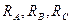, которые соединёны звездой. На рис. 3.5 указаны: фазные ЭДС генератора 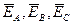, фазные напряжения нагрузки , , , 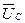линейные напряжения между линейными проводами Аа, Bb, Cc; линейные токи 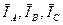, равные фазным токам; 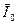- ток в нулевом проводе.

При симметричной нагрузке , . По первому закону Кирхгофа ток в нулевом проводе равен геометрической сумме токов фаз:

+ + .

Если принять нулевую точку генератора за условную точку нулевого потенциала, то потенциалы точек A,B,C будут равны фазным напряжениям , а линейные напряжения являются разностями потенциалов фазных напряжений:

; ; .

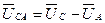Рис.4.1

 

Используя рис.4.1, выше приведённые выражения можно получить по второму закону Кирхгофа. Так, если , , , 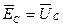то , , .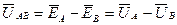

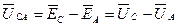На рис.4.2 изображена векторная диаграмма напряжений и токов при симметричной нагрузке.

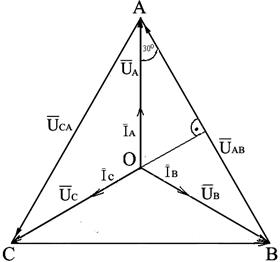
Рис.4.2

Из диаграммы следует: 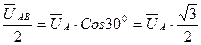. Соотношения между линейными и фазными напряжениями и токами при симметричной нагрузке: , .

Если активная нагрузка несимметрична, то . В нулевом проводе появится нулевой ток: + + .

Векторная диаграмма будет иметь вид:

Рис.4.3

На рис.4.4 приведена схема обрыва фазы А при симметричной нагрузке. На схеме указаны генераторные напряжения равные фазным напряжениям. Так как при обрыве фазы А ток 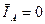, то ток в нулевом проводе .