Рис. 1.22
Решение
Составим систему уравнений по законам Кирхгофа:
I1 – I2 – I3 = 0
I1*R1 + I3*R3 = E1
I2*R2 – I3*R3 = E2
Используя среду MATLAB, запишем исходные данные сопротивлений в Омах и ЭДС в вольтах:
>> R1=2;
>> R2=1;
>> R3=2;
>> E1=60;
>> E2=30;
Используя систему уравнений, составим матрицу сопротивлений и вектор столбец ЭДС:
>> R=[1 -1 -1;2 0 2;0 1 -2]
R =
1 -1 -1
2 0 2
0 1 -2
>> E=[0;60;30]
E =
Определим токи в ветвях в амперах:
>> I=inv(R)*E
I =
7.9. Используя законы Кирхгофа и матричный метод расчёта, определить с помощью компьютера токи в цепи, представленной на рис.1.23, если заданы параметры: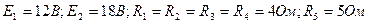 
. Решение выполнить в среде MATLAB для выражения 
.
Рис. 1.23
7.10. Используя законы Кирхгофа и матричный метод расчёта, определить с помощью компьютера токи в цепи, представленной на рис.1.24, если заданы параметры: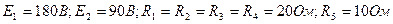 
. Решение выполнить в среде MATLAB для выражения .
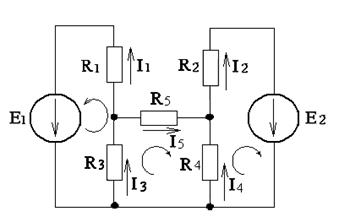
Рис. 1.24
7.11. В цепи, приведённой на рис.1.25, заданы значения 
. Выразить через эти величины мощность, выделяемую на нагрузке 
.
Рис. 1.25
7.12. Чему равны показания амперметра 
, вольтметров 
(рис.1.26), если разомкнуть тумблер 
.
Рис. 1.26
7.13. Напишите уравнение баланса мощностей для цепи, приведённой на рис.1.25.
7.14. В какой из трёх цепей, изображённых на рис.1.27, допущено короткое замыкание?
Рис. 1.27
7.15. В цепи, изображённой на рис.1.28, определить значение сопротивления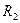 
при заданных параметрах 
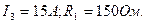
Рис. 1.28
7.16. Как изменится ток в цепи, приведённой на рис.1.29, после замыкания ключа.
Рис. 1.29
7.17. Сколько независимых контуров имеет схема, приведённая на рис.1.30.
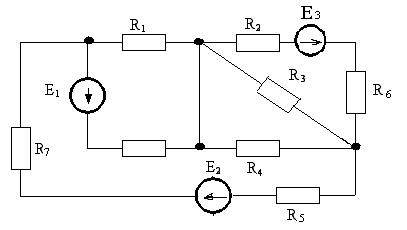
Рис. 1.30
7.18. В цепи, приведённой на рис.1.31, заданы значения . Выразить через эти величины мощность, выделяемую на нагрузке .
Рис. 1.31
7.19. Определить, какие из трёх источников ЭДС (рис.1.32) потребляют энергию, а какие – генерируют, если 
Рис. 1.32
2.2. ЛАБОРАТОРНАЯ РАБОТА №2
«ИССЛЕДОВАНИЕ НЕРАЗВЕТВЛЁННОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ, ИНДУКТИВНОСТЬЮ И ЁМКОСТЬЮ»
1. ЦЕЛЬ РАБОТЫ
1.1. Экспериментально проверить влияние на работу электрической цепи переменного тока активной, индуктивной и емкостной нагрузок при их последовательном соединении.
1.2. Определить условия резонанса напряжений.
2. ЭЛЕКТРООБОРУДОВАНИЕ И ПРИБОРЫ
2.1. Сеть однофазного переменного тока с частотой 50 Гц, напряжением 127 В.
2.2. Лабораторный автотрансформатор типа Э378, 0…250 В.
2.3. Ваттметр W электродинамической системы типа Д5004 (пределы измерения установить на напряжение 30В и ток 0,5А.)
2.4. Амперметр А электромагнитной системы типа Э8012 на ток 500 мА.
2.5. Вольтметр V электромагнитной системы типа Э8003 на напряжение 30В.
2.6. Вольтметр V1 электромагнитной системы типа Э8003 на напряжение 150 В.
2.7. Катушка индуктивности с числом витков w = 2400 и индуктивностью L = 0,77 Гн.
2.8. Магазин емкостей 0…34,75 мкФ.
2.9. Переключатель S на два положения.
2.10. Соединительные провода.
3. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Рассмотрим электрическую цепь переменного тока (рис. 2.1), состоящую из последовательно соединённых элементов 
Рис.2.1
Пусть мгновенный ток 
, тогда мгновенные напряжения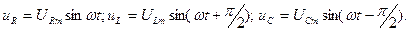 
Построим векторную диаграмму (рис.2.2) при условии, что действующие значения напряжений 
Рис.2.2
Из векторной диаграммы следует: 
, откуда действующее значение напряжения 
. Но 
, следовательно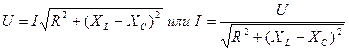 
. Введя обозначение полного сопротивления цепи 
, найдем действующее значение тока 
.
Разность между индуктивным и емкостным сопротивлениями называют реактивным сопротивлением цепи X = XL - XC. Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.3).
Рис.2.3
При XL > XC реактивное сопротивление положительно и угол сдвига фаз между током и напряжением 
> 0. 
.
Аналогично можно построить векторную диаграмму для действующих значений напряжений UL < UC (рис. 2.4) и треугольник сопротивлений (рис. 2.5).
Рис.2.4 Рис.2.5
При XL < XC реактивное сопротивление X отрицательно и угол < 0.
Если UL = UC и XL = XC, то векторную диаграмму можно представить в виде рис. 2.6, а зависимость тока от частоты в виде рис.2.7.
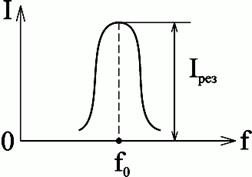
Рис.2.6 Рис.2.7
В этом случае наступает резонанс напряжений, когда ток в цепи совпадает по фазе с напряжением источника. При этом угол = 0, так как реактивное сопротивление равно нулю. При резонансе напряжений частота источника равна собственной частоте колебаний LC -контура. Если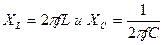 
, где f - частота источника питания, то можно записать 
. Решив это уравнение относительно f, получим 
.
На основании рисунков 2.6 и 2.7 следует, что признаками резонанса напряжений являются:
а) полное сопротивление цепи равно активному сопротивлению Z = R;
б) ток в цепи совпадает по фазе с напряжением источника и имеет максимальное значение;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности превышает напряжение источника;
г) коэффициент мощности cos = 1.
На рис. 2.8 изображены примерные функциональные зависимости индуктивных и емкостных напряжений, тока и коэффициента мощности в зависимости от изменения ёмкости конденсатора, где ср - резонансная ёмкость.
Рис.2.8
Количественная оценка соотношения энергий источника, катушки индуктивности и конденсатора при резонансе напряжений характеризуется добротностью контура:
.
Величину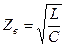 
при резонансе называют волновым сопротивлением контура.
Увеличив стороны треугольника сопротивлений в 
раз, получим треугольник мощностей (рис.2.9).
Рис.2.9
Мощность участков цепи, имеющей активное сопротивление, называется активной мощностью 
, которая измеряется в ваттах (Вт). Её вычисляют по формулам: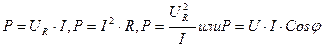 
. Последняя формула является основной, так как она применима к любой цепи переменного тока. Активная мощность характеризует безвозвратный расход энергии тока.
Мощность в участке цепи с индуктивным сопротивлением 
называется реактивной индуктивной мощностью 
, а в участке цепи с емкостным сопротивлением 
называется реактивной емкостной мощностью 
. Мощность характеризует энергию, временно накапливающуюся в магнитном поле индуктивности, а мощность характеризует энергию, временно накапливающуюся в электрическом поле конденсатора.
Реактивные мощности определяются по формулам: 
Общая реактивная мощность для цепи переменного тока с последовательно включенными 
определяется выражениями: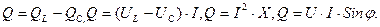 
Реактивную мощность измеряют вольт-амперами реактивными (вар).
Полная мощность 
и выражается в вольт-амперах (ВА). Из рис.2.9 видно, что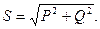 
Косинус угла сдвига фаз между током и напряжением в цепи переменного тока называется коэффициентом мощности, который может быть определён из выражений: 
Значение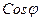 
может изменяться от нуля до единицы в зависимости от соотношения между активным и реактивным сопротивлениями.
Если в цепи имеется только реактивное сопротивление, то угол 
и мощность в цепи чисто реактивная. Если же имеется только активное сопротивление, то 
, при этом полная мощность в цепи чисто активная.
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
4.1. Ознакомиться с электрооборудованием и электроизмерительными приборами, необходимыми для выполнения работы.
4.2. Собрать электрическую схему (рис.2.10) и предъявить её для проверки преподавателю или лаборанту.
Рис.2.10 
4.3. Включить выключатель сети 
. С помощью ЛАТРа установить напряжение в цепи 20В.
4.4. Постепенно изменяя ёмкость С от 10мкФ до 20мкФ через 1мкФ снять показания приборов, которые необходимо записать в графу «Измерено» табл. 2.1. С помощью подборки емкостей добиться максимального тока, соответствующего резонансу напряжений цепи.
Таблица 2.1
4.5. Использовать для вычисления следующие формулы:
- полное сопротивление катушки; 
- активное сопротивление катушки; 
- индуктивное сопротивление катушки в омах; 
- индуктивность катушки в генри,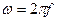 
- угловая частота 
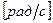при частоте питающей сети 
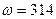
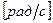; емкостное сопротивление 
- где ёмкость 
измеряется в фарадах 
; 
- полное сопротивление цепи;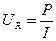 
- напряжение на активном сопротивлении катушки; 
- индуктивное напряжение катушки; - полная мощность цепи; 
- коэффициент мощности, 
; 
- реактивная мощность.
4.6. Для определенной части таблицы по заданию преподавателя для опытов φ < 0 (при емкостном характере нагрузки), φ = 0 (при резонансе напряжений),
φ > 0 (при индуктивном характере нагрузки) построить в выбранном масштабе векторные диаграммы напряжений (три диаграммы) и соответствующие им треугольники сопротивлений и мощностей.
4.7. По данным таблицы построить в масштабе графики зависимостей:
; 
; 
.
4.8. Данные всех измерений предъявить для проверки преподавателю и с его разрешения схему разобрать. Получить задание по п.4.6.
4.9. Привести в порядок рабочее место.
5.СОДЕРЖАНИЕ ОТЧЕТА
5.1. Номер, наименование и цель работы.
5.2. Основные технические данные потребителей и электроизмерительных приборов.
5.3. Принципиальная электрическая схема (рис.2.10).
5.4. Таблица наблюдений и вычислений.
5.5. Формулы, по которым велись вычисления.
5.6. Векторные диаграммы напряжений, треугольники сопротивлений и мощностей с указанием масштаба для случаев XL>XC;. XL=XC; XL<XC.
5.7. Графики зависимостей по п.4.7 порядка выполнения работы.
5.8. Краткие выводы по работе, в которых дать ответы на следующие
вопросы:
а) как изменяются параметры цепи с изменением ёмкости в цепи при последовательном соединении R, L и C?
б) какими способами можно получить резонанс напряжений?
в) где используется резонанс напряжений?
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Дайте определения понятий амплитудного, действующего, мгновенного и среднего значений периодического синусоидального тока.
6.2. Приведите выражения, связывающие амплитудное, действующее и среднее значения периодического синусоидального тока.
6.3. Дайте определение частоты и периода переменного тока, и укажите, в каких единицах они измеряются.
6.4. Что называется начальным фазовым углом и углом сдвига фаз?
6.5. Какие значения переменного тока и напряжения показывают измерительные приборы?
6.6. Как определить по графику, какая из синусоидальных величин опережает по фазе другую?
6.7. Как перейти графически от синусоидальной кривой к векторной диаграмме и наоборот?
6.8. Найдите графически сумму двух периодических синусоидальных токов одинаковой частоты. Найдите действующее значение и начальную фазу суммарного тока.
6.9. Построить векторную диаграмму суммы 3-х напряжений.
6.10. Какой из приведенных графиков (рис. 2.11) характеризует цепь переменного тока, в которую включено только одно активное сопротивление? Приведите векторную диаграмму для такой цепи.
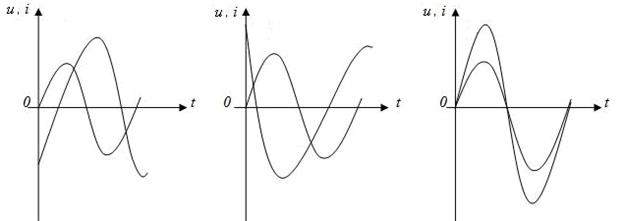
Рис. 2.11
6.11. Что представляет собой индуктивные и емкостные сопротивления и какова их физическая природа?
6.12. Объясните, почему при постоянном токе включение в цепь конденсатора равносильно разрыву цепи, а при переменном токе ток через емкость проходит.
6.13. Параметры катушки индуктивности R и L известны. Чему равно сопротивление катушки постоянному току?
6.14. Какой из приведенных графиков (рис. 2.12) характеризует цепь переменного тока, в которую:
а) включена только индуктивность?
б) включена только ёмкость?
Приведите векторные диаграммы для таких цепей.
Рис.2.12
6.15. Почему при последовательном соединении R, L и C приложенное напряжение равно геометрической сумме падений напряжений, а не алгебраической?
6.16. Как выражается закон Ома для цепей переменного тока с последовательным соединением R, L и C?
6.17. Приведите графики мгновенных значений токов и напряжений для цепей переменного тока, имеющих:
а) индуктивный характер?
б) емкостной характер?
6.18. Приведите векторные диаграммы для цепей переменного тока, имеющих: а) индуктивный характер?
б) емкостной характер?
6.19. Начертите треугольники напряжений, сопротивлений и мощностей для цепи с индуктивным и активным сопротивлениями.
7. ВОПРОСЫ К ЗАЩИТЕ
7.1. Определить действующее значение тока в цепи R = 8 Ом; Xc = 6 Ом; U = 100B (см. рис. 2.13).
7.2. Определите активную и реактивную мощности (см. рис. 2.13), если Xc = 10 Ом; R = 10 Ом; U = 100 В.
7.3. Найти полное сопротивление и угол сдвига по фазе между током и напряжением цепи (см. рис. 2.13), если Xc = 10 Ом; R = 10 Ом; U = 100 В.
Рис.2.13
7.4. В цепи с последовательным соединением R, L, C ток I = 10А, напряжения U = 200В, UL= UC = 300В. Найти реактивную мощность.
7.5. Действующие значения напряжений соответственно равны U = 200В, UL=UC=100 В.
Найти UR (см. рис.2.14).
Рис. 2.14
7.6. Дано: X L= 2 Ом, ХС = 5 Ом, R = 3 Ом. Показать взаимное расположение векторов тока и напряжений в этой цепи. Чему равен 
(см. рис. 2.15)?
Рис. 2.15
7.7. Дано: R = 3 Ом, Х = 4 Ом, U = 100 В. Определить падение напряжения на активном сопротивлении (см. рис. 2.16).
7.8. Вычертить электрическую цепь с последовательно включенными элементами, которой соответствует векторная диаграмма, представленная на рис. 2.17.
Рис. 2.16 Рис. 2.17
7.9. Имеется цепь с последовательным соединением R, L, C, находящихся в состоянии резонанса при частоте f0 = 5 Гц. Как изменится векторная диаграмма, если f > f0 и f < f0?
7.10. Построить векторную диаграмму, соответствующую цепи, представленной на рис. 2.18.
Рис. 2.18
7.11.Определить реактивное сопротивление цепи, если ХL = 5 Ом, ХС = 10 Ом.
7.12. Действующие значения напряжений на индуктивности и ёмкости соответственно равны: UL = 200 B, UC =100 B, найти Uав (см. рис. 2.19).
Рис. 2.19
7.13. Определить угол сдвига по фазе между током и напряжением в цепи, изображенной на рис. 2.18, если = 4 Ом, R = 4 Ом.
7.14. Найти в общем виде полное сопротивление цепи (см. рис. 2.20).
Рис. 2.20
7.15. Как взаимно расположены вектора токов и приложенного напряжения в цепи, приведённой на рис. 2.21, если XL =5 Ом, XC = 2 Ом, R = 3 Ом?
Рис. 2.21
7.16. Мощность, потребляемая электрической цепью равна 100 Вт. Действующее значение тока в цепи I = 2 А. Чему равно активное сопротивление цепи?
7.17. Дано: U ав = U cd = 100B. Найти угол φ (см. рис. 2.22)
Рис. 2.22
7.18. Дано: R = XL = 1Ом, u = 
sin ωt. Определите ток в цепи, изображенной на рис.2.23.
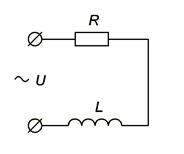
Рис. 2.23
7.19. Определить полную мощность в цепи, если в ней U=100B, I=10A, cosφ=0,5.
2.3. ЛАБОРАТОРНАЯ РАБОТА № 3
«ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ, ИНДУКТИВНОСТЬЮ И ЁМКОСТЬЮ»
1.ЦЕЛЬ РАБОТЫ
1.1. Изучить сущность процессов, при которых включение конденсаторов параллельно потребителю, обладающего индуктивностью, приводит к повышению коэффициента мощности электротехнического устройства.
1.2. Опытным путем проверить условия резонансов токов.
2. ЭЛЕКТРООБОРУДОВАНИЕ И ПРИБОРЫ
2.1. Сеть однофазного переменного тока с частотой 50Гц, напряжением 127В.
2.2. Лабораторный автотрансформатор (ЛАТР) типа Э378, 0…250В.
2.3. Ваттметр электродинамической системы типа Д5004 (пределы измерения установить на 30В, токовую клемму использовать на 0.5А).
2.4. Амперметр А электромагнитной системы типа Э8021 на 100мА.
2.5. Амперметры А1 и А2 электромагнитной системы типа Э8021 на 500мА.
2.6. Вольтметр V электромагнитной системы типа Э8003 на 150В.
2.7. Катушка индуктивности с числом витков w=2400, L=0, 77 Гн.
2.8. Блок конденсаторов 10…20 мкФ.
2.9. Соединительные провода.
3. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Рассмотрим разветвленную цепь c активным сопротивлением, индуктивностью и ёмкостью, приведённую на рис.3.1.
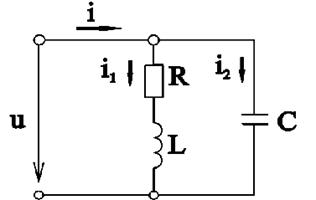
Рис.3.1
Пусть мгновенные значения напряжения и тока изменяются по синусоидальному закону 
. По первому закону Кирхгофа 
, для действующих значений токов 
. По закону Ома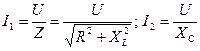 
. Из треугольника сопротивлений 
Разложим токи в ветвях на активные и реактивные составляющие IR, IL, IC. 
.
Введем следующие обозначения:
= g - активная проводимость первой ветви;
- реактивная индуктивная проводимость первой ветви;
- реактивная емкостная проводимость второй ветви. Для случая IL > IC построим векторную диаграмму (рис.3.2).
