Методы перевода чисел из одной системы счисления в другую

Рассмотрим вначале методы перевода чисел из смещенной системы счисле- ния с основанием k ₁ в смещенную систему с основанием k ₂. Через будем обозначать число X в k ₁ - й системе.

Правая часть выражения (2) определяет правило вычисления количествен- ­ного эквивалента числа, записанного в форме (1). На этом основан один из ме­то- дов перевода чисел. Для перевода числа в систему с основанием k ₂необходимо записать в форме (2); заменить цифры х_i и основание k ₁их k ₂ - ми эквива­лен- тами, а затем вычислить выражение (2) по правилам системы счисления с осно- ванием k ₂.

Пример 1. Перевести число X₍₂₎ = 1011,1001 в десятичную систему счис­ле-ния

Описанный метод перевода чисел из одной системы в другую получил наз- ва­ние метода непосредственного замещения. Этот метод удобно использовать в случае, когда k ₁< k ₂ и при переводе чисел в такую систему, где просто выполняя- ются операции сложения и умножения (например, из двоичной системы в десятич-ную). Для упрощения вычисления при этом можно воспользоваться таким выра- жени­ем, полученным из (2):

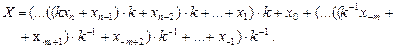
Однако при переводе чисел в системы с «непривычными» основаниями, осо­бенно в случае k ₁> k ₂,применение этого метода связано с довольно громозд- кими вычислениями. Поэтому во многих случаях удобнее пользоваться отдельными ме­тодами перевода целых чисел и правильных дробей.

Метод перевода целых чисел из системы с основанием k ₁всистему с осно- ва­нием k ₂(k ₁> k ₂) заключается в следующем. Число делят на k ₂поправилам деления с основанием k ₁до получения остатка. Если частное от деления не нуль, то частное становится делимым и процесс деления на k ₂продолжают. Как толь- ко очередное частное станет равным нулю, процесс деления на k ₂ прекращают. Оста­ток, полученный при первом делении на k ₂ , представляет цифру разряда резуль­тата с весом , остаток от второго деления представляет цифру результата с ве­сом 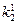,и т. д. Последний остаток является старшей цифрой результата.

Пример 2. Перевести число Х ₍₁₀₎ = 1247 в пятеричную систему счисления.

В случае, когда k ₁< k ₂, выполняют умножение цифры с весом , числа (старшей цифры числа ) на основание k ₁, после чего к произведению прибав­- ляют следующую (в порядке убывания весов) цифру числа . Результат преды­дущей операции умножают на k ₁и прибавляют очередную цифру числа . Этот процесс заканчивают, когда будет прибавлена цифра с весом (младшая цифра). Все вычисления при этом выполняются в k ₂-й системе счисления.

Пример 3. Перевести из двоичной системы в троичную число Х ₍₂₎ = 10110110.

Перевод правильных дробей из системы счисления с основанием k ₁всис- тему с основанием k ₂ (k ₁> k ₂ ) осуществляется так. Дробь, соответствующая числу , умножается на k ₂ по правилам умножения в системе с основанием k ₁ . В по­лученном произведении отделяется целая часть, которая может быть равной ну- лю, а дробная часть снова умножается на k ₂с последующим отделением целой части. Эти операции повторяют либо до получения нулевой дробной части произ- веде­ния, либо до получения необходимого количества разрядов числа в новой системе счисления. Старшая цифра результата перевода (т. е. первая после за­пятой) совпадает с первой отделенной целой частью, вторая цифра результата—со второй отделенной целой частью и т. д.

Пример 4. Перевести число Х ₍₁₀₎ = 0,314 в двоичную систему счисления, ограничившись шестью разрядами после запятой.

 

При k ₁< k ₂ для перевода правильной дроби, имеющей т цифр после запя- той, необходимо разделить цифру младшего разряда числа на k ₁ и сложить со сле­дующей цифрой этого числа. Такую операцию необходимо повторить еще т –1 раз, используя на каждом шаге в качестве делимого сумму, полученную на пре- ды­дущем шаге. Все операции выполняются в k ₂-й системе.

Пример 5. Перевести в десятичную систему число Х ₍₂₎ = 0,101101.

 

 

Перевод чисел в симметричные и кососимметричные системы счисления с ос­нованием k ₂можно осуществить в три этапа. На первом этапе, используя рас- смот­ренные выше правила, осуществляется перевод чисел в смещенную систему счис­ления с основанием k ₂ . На втором этапе цифры k ₂-й смещенной системы, ко- торые отсутствуют в симметричной и кососимметричной системе, представляются двумя цифрами симметричной или кососимметричной системы, в которую осуще-ствляется перевод. На третьем этапе осуществляется суммирование всех допусти- мых для симметричной или кососимметричной системы цифр, полученных на пер- вом и втором этапе, с учетом их весов по правилам этих систем счисления.

Пример 6. Перевести число Х ₍₁₀₎ = 1247 в пятеричную каноническую сим­метричную систему счисления.

После выполнения первого этапа (см. пример 2) получим Х _{5) = 14442. По­сколь- ку допустимыми для симметричной системы счисления являются цифры {-2, -1, 0, 1, 2}, то цифру 4 представляем двумя цифрами симметричной систе­мы следую- щим образом: 4 = . На третьем этапе осуществляем суммирование. Результат суммирования является числом 1247, представленным в пятеричной симметричной системе счисления.

Для перевода чисел из симметричных и кососимметричных систем в сме- щен­ные системы достаточно просуммировать цифры числа в исходной системе с учетом их знаков и весов.

Пример 7. Перевести в десятичную смещенную систему число .

Перевод чисел из канонических систем в квазиканонические системы и об- рат­ный перевод выполняются аналогично.

Для преобразования нечетного положительного числа из k ₁-й системы счи- сле­ния в двоичную систему с цифрами {1, } необходимо вначале перевести это число в двоичную систему с цифрами {0, 1). Затем, просматривая полученную запись слева направо, необходимо выделить все группы цифр вида 00...01, даже если они включают один нуль. Эти группы необходимо заменить на группы вида . Остальные цифры 1 остаются без изменения. При преобразовании нечетных от-рицательных чисел группы цифр 00...01 необходимо заменить на группы 1...11, остальные цифры 1 заменить на .

Пример 8. Перевести число X ₍₁₀₎= 0,314 в двоичную систему с цифрами (1, }. Используя результат примера 4, получим:

X ₍₂₎= 0,0101000001; = 0,1 1 1 .

Обратный перевод выполняется так же, как и перевод из симметричных систем в смещенные.

Методы перевода чисел из систем с основанием 2 ^r в двоичную систему и наобо­рот очень просты, чем и объясняется широкое использование этих систем для ввода и вывода информации в ЭВМ. Для перевода числа из системы счисления с основанием 2 ^r в двоичную систему необходимо представить каждую цифру систе­- мы с основанием 2 ^r посредством r двоичных разрядов.

Пример 9. Перевести числа X ₍₈₎ = 762,15 и Y ₍₁₆₎ = Е51А,7D в двоичную сис-тему счисления.

X ₍₂₎ = 111110010,001101; Y ₍₂₎ =1110010100011010,01111101.

Для перевода двоичного числа в систему счисления с основанием 2 ^r необхо­димо, двигаясь от запятой влево и вправо, разбить двоичное число на группы, со- держащие no r разрядов, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из r двоичных разрядов необходимо заме­- нить цифрой системы счисления с основанием 2 ^r.

Пример 10. Перевести число Х _{2) = 11111101, 1000001 в шестнадцатирич- ную систему счисления

Высокая скорость перевода чисел может быть достигнута с помощью таб- личных методов. В простейшем случае применения этих методов в памяти ЭВМ хра­нится таблица соответствия между всеми числами в системах счисления с осно- ва­ниями k ₁и k ₂, а перевод сводится к обращению к нужной ячейке памяти. Однако размеры таблицы и занимаемый ею объем памяти часто оказы­ваются технически неприемлемыми. Поэтому с целью уменьшения занимаемого объема памяти в ней хранят только таблицы соответствия цифр за­данных систем счисления и весов их разрядов. Перевод чисел осуществляется пу­тем обращения к этим таблицам и выполнения операций сложения и умножения в системе с основанием k ₂(как и по методу непосредственного замещения}. Если числа в системе с основанием k ₁представлены п ₁разрядами, то по пер­вому варианту размерность хранимой таблицы определяется строками, а по второму k ₁+ п ₁+1 строками.

В позиционных системах с отрицательным основанием k < –1 представле­ние любого рационального числа имеет вид

где x_i – цифры i -го разряда. Отсюда следует, что веса отдельных разрядов в таких системах образуют ряд

На этом основан один из методов перевода чисел из системы с основанием k ₁в систему с отрицательным основанием k ₂< -1. Сначала число переводят в си­с- тему с положительным основанием k ₂ . Затем число разделяют на два числа А и B. При положительном числе разряды числа А с четным i (в том числе и i = 0) равны разрядам числа с таким же i, а разряды числа А с нечетным i равны нулю.

Разряды числа В с четным i равны нулю, а в разрядах с нечетным i каждая не равная нулю цифра заменяется единицей в i +1-м разряде и цифрой |k| - x_i. После этого необходимо выполнить суммирование чисел A и В с учетом того, что переносы из разрядов с четным i имеют знак «+», а из разрядов с нечетным i – знак «–». Перенос из последнего (n -го) разряда чисел А и В заменяется цифрами 1 и | k |– 1 соответственно в п + 2-м и п + 1-м разрядах.

Если же число отрицательное, то разряды числа А с четным i при заменяются единицей в i+ 1-м разряде и цифрой |k| – x_i в i -м разряде. Нечет­- ные разряды числа А равны нулю. Разряды числа В с четным i равны нулю, а раз- ­ряды с нечетным i равны i -м разрядам числа . Суммирование чисел также должно осуществляться с учетом знаков переносов.

Пример 11. Перевести числа X ₍₁₀₎ = 30,75 и Y ₍₁₀₎ = – 23,5 в систему с ос­но- ванием k ₂= – 2. В системе с основанием 2 указанные числа будут представ­лены как X ₍₂₎ = 11110,11 и Y ₍₂₎= – 10111,1.

 

1 1 1 1 0, 1 1 1 0 1 1 1, 1

 

Таким образом, X _(-2) = 1100011,11; Y _(-2) = 111001,1.

Для перевода числа в систему с положительным основанием k ₂ , необхо­димо также разделить на два числа А и B. При этом четные разряды числа А равны четным разрядам , нечетные разряды числа А равны нулю. Число В имеет в нечетных разрядах те же цифры, что и число в нечет­ных разрядах. Четные разряды В равны нулю. Далее, из А следует вычесть В, если положительное, или же из В вычесть А, если отрицатель­ное. Знак определяется знаком веса старшего разряда.

Пример 12. Перевести в систему с положительным основанием числа X _(-2) = 10100,1101 и Y _(-2) = 101101,10101. Первое из этих чисел положительное, так как его старший разряд имеет вес 2⁴, а второе число отрицательное – вес его стар- ­шего разряда равен 2⁵.

Другие методы перевода чисел всистемы с отрицательным k основаны на пос­ледовательном делении целого числа на основание ина последовательном ум- ноже­нии дробей на основание. Припереводе целых чисел все остатки от деления и припереводе дробей целые части получаемых произведений должны быть по- ложитель­ными, меньшими k. Для выполненияэтих требований при переводе дро- бей дробная часть D, используемая на каждом шаге перевода, должна удовлетво- рять условию

Перевод чисел из позиционной системы в СОК в простейшем случае вы- полня­ется путем деления числа X на модули Р_i (i = ). Наименьшие положи- тельные остатки от такого деления и образуют представление X в СОК. Однако такой ме­тод перевода часто оказывается малоэффективным из-за большого числа операций деления.

Другие методы перевода из позиционных систем в СОК основаны на ис- пользо­вании следующих свойств чисел, представленных остатками:

 

rest (A+B) (mod P_i) = (rest A (mod P_i) + rest B (mod P_i)) (mod P_i),

rest AB (mod P_i) = (rest A (mod P_i) x rest B (mod P_i)) (mod P_i). (4)

 

Пусть для заданного набора модулей Р_i (i = )и позиционной k -ичной системы известны представления в остатках любой степени основания

k ^j = (k _{1 j}, k _{2 j}, …, k _{m j}), (j = ),

а также любой k -ичной цифры

x_j = (x _{1 j} , x _{2 j} , …, x _{m j} ), (j = ).

Тогда

X_i = rest X (mod P_i) = rest (mod P_i) =

= (rest x_j (mod P_i) rest k ^j (mod P_i)) (mod P_i) = (x_{i j} k _{i j} (mod P_i)) (mod P_i).

Таким образом, для нахождения остатка числа X по модулю P_i, необходи- мо сложить попарные произведения остатков цифр x_j и весов k ^j. При этом все сложе­ния и умножения выполняются по модулю P_i.

Рассмотренный метод перевода применяется и в другом варианте, исполь- зующем не только свойства (4), но и следующее свойство:

 

rest AB (mod P_i) = (A rest B (mod P_i)) (mod P_i).

 

В этом случае для вычисления Х_i достаточно иметь представление в остат- ках либо только степеней основания k^j, либо только цифр х_j, т.е.

X_i = (x _j k _{i j} (mod P_i)) (mod P_i) = (x_{i j} k ^j (mod P_i)) (mod P_i). (5)

Пример 13. Перевести число X ₍₁₀₎= 839 в СОК с модулями Р ₁= 3, Р ₂ = 5, Р ₃ = 7, P ₄=11. Для степеней основания и заданных цифр позиционной десятич- ­ной системы имеем

10²= (1, 0, 2, 1); 8 = (2, 3, 1, 8);

10¹=(1, 0, 3, 10); 3 = (0, 3, 3, 3);

10⁰= (1, 1, 1, 1); 9 = (0, 4, 2, 9).

Далее находим остатки X_i:

Х ₁= (1ּ2 +1ּ0 +1ּ0) (mod 3) = 2;

X ₂ = (0ּ3 + 0ּ3 + 1ּ 4) (mod 5) = 4;

Х ₃= (2ּ1 + 3ּ3 +1ּ2) (mod 7) = 6;

Х ₄= (1ּ8 +10ּ3 +1ּ9) (mod 11) = 3.

 

Следовательно, X = (2, 4, 6, 3). Такой же результат получается и при ис- пользовании формул (5).

Наиболее простой и естественный путь перевода чисел из СОК в позици- онную систему, состоящий в решении системы уравнений вида

 

X = l ₁ P ₁ + X ₁; X = l ₂ P ₂ + X ₂, …; X = l_i P_i + X_i,

 

на практике не может быть использован, так так число неизвестных X, l ₁, l ₂ , …, l_m здесь больше числа уравнений и, следовательно, система уравне­ний имеет беско- нечное множество решений. Поэтому для этих целей используются более сложные методы, обеспечивающие однозначность перевода.

Метод ортогональных базисов основан на использовании констант (ортого­нальных базисов) В ₁ , В ₂ , …, В_m , представление которых в СОК при заданном на­боре модулей P_i (i = ) имеет вид

В ₁ = (1, 0, 0, …, 0);

В ₂ = (0, 1, 0, …, 0);

…………………...;

В_m = (0, 0, 0, …, 1).

Представление числа X в позиционной k -ичной системе в этом случае мо- жет быть получено следующим образом:

 

где . Для фиксированного набора модулей Р_i k -ичные представления констант B_i(k) могут быть вычислены заранее по формуле

B_i(k) = .

Здесь — вес i -го ортогонального базиса, выбираемый из условия

rest (mod P_i) = 1.

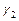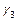Пример 14. Перевести в десятичную систему число X = (2, 3, 4, 5), пред­ставленное в СОК с основаниями Р ₁= 3, Р ₂ = 5, Р ₃ = 7, Р ₄ = 11. В этом случае N = 3ּ5ּ7ּ11 = 1155; = 1, = 1, = 2, = 2; В ₁= 385, B ₂= 231, B ₃ = 330, B ₄ = 210. Следовательно,

X ₍₁₀₎ = 2ּ385 + 3ּ231 + 4ּ330 + 5ּ210 (mod 1155) = 3833 (mod 1155) = 368.

Кроме метода ортогональных базисов для перевода чисел из СОК в пози- цион­ную систему используются также методы, основанные на промежуточном представ­лении числа в полиадической системе счисления. В такой системе при за-данном наборе модулей P_i (i = )вес q_i каждого i- горазряда равен q_{i -1} P_i,a q _o = 1. Поэтому представление числа X в полиадической системе имеет вид

,

где b_i — цифры полиадической системы. При переводе из СОК b ₀= Х ₁,а осталь- ные цифры b_i вычисляются по формулам

b_i = rest a_i (mod P_{i +1}),

,

.

 

Здесь – цифра b_{i -1},представленная остатками по всем основаниям, номер которых выше номера i –1; – так называемая формальная обратная величина модуля P_i по основаниям Р_j; (i ≠ j). Остатки , которыми в СОК пред­ставляется формальная обратная величина P_i, выбираются из условия

rest P_i (mod Р_j) = 1.

 

Пример 15. Перевести из СОК с основаниями Р ₁= 5, Р ₂ = 9, Р ₃= 11 в де­сятичную систему число X = (3, 6, 10). Перед вычислением цифр b_i полиадичес- кой системы найдем формальные обратные величины модулей Р_ij . Из условий

rest 5 P ₁₂ (mod 9) = 1; rest 9 P ₂₁ (mod 5) = 1;

rest 5 P ₁₃ (mod 11) = 1; rest 9 P ₂₃ (mod 11) = 1

 

следует Р ₁₂ = 2, P ₁₃= 9; Р ₂₁ = 6, Р ₂₃= 5. Кроме того, b ₀= 3, = (3, 6, 10); = (3, 3, 3); = (0, 2, 9).

Следовательно, а _1(С0К) = ((3, 6, 10) - (3, 3, 3)) (0, 2, 9) = (0, 3, 7) (0, 2, 9) = (0,6, 8),

 

b ₁ = rest a ₁ (mod 9) = 6;

а _2(С0К) = ((0, 6, 8) - (0, 6, 6)) (6, 0, 5) = (0, 0, 2) (6, 0, 5) = (0,0, 10),

 

b ₂ = rest a ₂ (mod 11) = 10.

 

Таким образом, X ₍₁₀₎ = b ₀ + b ₁ P ₁ + b ₂ P ₁ P ₂ = 3 + 6ּ5 + 10ּ5ּ9 = 483.