Построение десятичных ЭВМ, в которых цифры отображались бы сигналами, квантованными по десяти уровням, является практически целесообразным только при наличии технических средств (схем) для представления чисел, основные технико-экономические характеристики которых (стоимость, надежность, быстродействие и др.) были бы не хуже соответствующих характеристик схем для представления двоичных цифр. Однако, как правило, некоторые основные характеристики известных схем для такого представления десятичных цифр уступают характеристикам двоичных схем. Поэтому при построении десятичных ЭВМ исполь-зуется кодирование двоичными цифрами десятичных цифр.
Для кодирования цифр k -ичной системы счисления двоичными цифрами не-обходимо иметь не менее ] Iog2 k [двоичных разрядов. Здесь и далее запись ] А [означает округление A в сторону ближайшего большего целого числа, если А дробное. Если считать, что числа, с которыми оперирует ЭВМ, не превосходят N, то относительное увеличение количества оборудования, необходимого для представле-ния k -ичных чисел при их двоичном кодировании, оценивается функцией
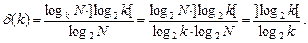
Функция 
= 1, если k = 2 r, r = 1, 2,... В таком случае для представле- ния чисел в двоичной и k -ичной системах требуется одинаковое количество обору- дования. При k 
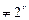функция > 1. Например, в случае k =10
т.е. в двоично-кодированной десятичной системе (двоично-десятичной системе) тре-буется примерно в 1,2 раза больше оборудования для представления чисел по сравнению с двоичной системой.
Очевидно, что любой k -ичной цифре можно поставить в соответствие лю- бое из 2 h двоичных чисел, записываемых с помощью h разрядов. Следовательно, чис-ло способов двоичного кодирования k цифр равно числу размещений из 2 h по k,т.е. 
. Это число очень быстро растет с увеличением k, что делает не- возможным анализ ручными методами всех способов двоичного кодирования даже для практически наиболее важного случая k = 10. В связи с этим к настоящему времени исследованы далеко не все способы кодирования десятичных цифр.
Наиболее широкое распространение в ВТ получили двоично-десятичные системы счисления, в которых десятичные цифры записываются как четырехраз-рядные двоичные числа – двоичные тетрады. Иногда используется также представ-ление десятичных цифр с помощью пяти, шести и семи разрядов. В принципе можно построить ЭВМ, работающую при любом двоично-десятичном кодирова- нии. Однако, как показывают теоретические исследования и опыт разработки де- сятичных ЭВМ, наилучшие результаты могут быть получены при использовании двоично-десятичных кодов (ДДК), обладающих свойствами единственности, упо-рядоченности, четности, дополнительности и взвешенности (эти свойства называ-ются также условиями Рутисхаузера).
ДДК обладает свойством единственности, если между десятичной цифрой и комбинацией двоичных цифр установлено взаимно однозначное соответствие. Данное свойство обеспечивает возможность работы с ДДК и облегчает процесс декодирования.
Упорядоченность ДДК состоит в выполнении одного из условий
0 (2) < 1 (2) < … < 9 (2);
0 (2) > 1 (2) > … > 9 (2)
для двоичных представлений 0 (2) , 1 (2) , …, 9 (2) десятичных цифр 0, 1,..., 9. Нали- чие упорядоченности ДДК необходимо для реализации логических операций.
Свойство четности ДДК должно проявляться в том, чтобы всем четным десятичным цифрам соответствовали либо только четные, либо только нечетные двоичные числа. Аналогично всем нечетным десятичным цифрам должны соот-ветствовать либо только нечетные, либо только четные двоичные числа. Это свой- ство упрощает выполнение операций умножения, деления и округления.
Сущность свойства дополнительности ДДК заключается в следующем. Если сумма двух десятичных цифр равна 9, то переход от двоичного представления од- ной цифры к двоичному представлению другой должен осуществляться путем инвертирования (т. е. замены 0 на 1 и наоборот) двоичных разрядов. Это облег- чает формирование обратного и дополнительного кодов, используемых при опера- ции алгебраического сложения.
ДДК называется взвешенным, если каждому из h разрядов двоичного пред-ставления xhxh -1 … x 1 десятичной цифры X поставлены в соответствие веса ah, ah -1 , …, a 1 , причем
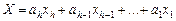(3)
Использование взвешенных ДДК облегчает выполнение логических опера- ций и перевод чисел из одной системы счисления в другую.
ДДК, получающиеся друг из друга простой перестановкой весов ai, обра- зуют кодовую группу, или просто группу. Существует 86 групп взвешенных ДДК, обладающих свойством единственности, в которых для представления десятичных цифр используются двоичные тетрады. Среди них есть ДДК, имеющие только положительные веса, и ДДК с одной или двумя отрицательными весами, напри- мер, «8, 4, 2, 1», «8, 4, 2, -1», «6, 3, -1, -1».
Свойством дополнительности обладают все взвешенные ДДК с положительными весами, у которых сумма весов равна девяти. Существуют четыре груп- пы взвешенных ДДК, обладающих одновременно свойствами единственности и дополнительности, а именно: «5, 2, 1, 1», «4, 3, 1, 1», «4, 2, 2, 1», «3, 3, 2, 1». Среди ДДК с отрицательными весами свойствами единственности и дополнительности обладают девятнадцать групп кодов, приведенных в табл. 2.
Таблица 2
| Номер группы | Веса разрядов | Номер группы | Веса разрядов |
| 8 4 3 -6 | 6 3 2 -2 | ||
| 8 4 2 -5 | 6 3 1 -1 | ||
| 8 3 2 -4 | 6 2 2 -1 | ||
| 7 5 3 -6 | 5 4 3 -3 | ||
| 7 5 1 -4 | 5 3 2 -1 | ||
| 7 3 1 -2 | 4 4 3 -2 | ||
| 6 5 2 -4 | 4 4 2 -1 | ||
| 6 5 1 -3 | 8 6 –1 -4 | ||
| 6 4 2 -3 | 8 4 –2 -1 | ||
| 6 4 1 -2 |
Свойством упорядоченности могут обладать только ДДК, не имеющие от-рицательных весов. Одновременно свойствами единственности, дополнительности и упорядоченности обладают взвешенные ДДК «5, 2, 1, 1», «5, 1, 2, 1», «4, 3, 1, 1» и «3, 3, 2, 1».
Всеми перечисленными выше свойствами обладают коды «2, 4, 2, 1» и «4, 2, 2, 1» (табл. 3), которые получили название кодов Эмери. Код «2, 4, 2, 1» впервые был использован в швейцарской ЭВМ, а затем получил достаточно широкое распространение в ВТ. Благодаря свойству дополнительности ДДК «2, 4, 2, 1» и «4, 2, 2, 1» переход к обратному и дополнительному кодам осуществляется легко, однако искусственный порядок весов несколько затрудняет выполнение арифметических операций.
Таблица 3
| Десятичные цифры | Двоично-десятичные коды | ||||||||||
| «8,4,2,1» | «2,4,2,1» | «4,2,2,1» | «7,4,2,1» | «5,4,2,1» | «С избыт-ком 3» | «3 a + 2» | «2 из 5» | «2 из 7» | «Рефлек-сный» | «w,x,y,z» | |
Распространенным в ВТ ДДК является взвешенный код «8, 3, 2, 1», назы- ваемый также кодом прямого замещения (табл. 3). Этот код образуется путем за- писи десятичных цифр в двоичной позиционной системе счисления с естественным порядком весов и обладает всеми перечисленными выше свойствами, кроме свой- ства дополнительности. Последнее делает код неудобным при реализации опера- ции алгебраического сложения из-за трудностей формирования переносов из млад- шей тетрады в старшую. Однако код «8, 4, 2, 1» удобен для машинного перево- да чисел из десятичной системы в двоичную и обратно.
В каждом конкретном случае применение какого-либо ДДК обуславлива- ется определенными его преимуществами по сравнению с другими ДДК. Напри- мер, взвешенный код «7, 4, 2, 1», приведенный в табл. 3, применялся в элект- ро-механических вычислительных машинах, где двоичной единице соответствова- ло замкнутое реле, а двоичному нулю – разомкнутое реле, причем замкнутое реле потребляло ток от источника питания. В рассматриваемом коде использованы комбинации с минимальным числом единиц, что обеспечивает минимальное по-требление тока от источника питания.
Близким по своим свойствам к коду «7, 4, 2, 1» является код «5, 4, 2, 1» (табл. 3). Десятичные числа, записанные в этом коде, можно рассматривать как двоично-пятеричные с кодированным представлением цифр. Три младших двоич- ных разряда в каждой тетраде изображают один пятеричный разряд, а старшая двоичная цифра соответствует двоичному разряду. Этот код имеет ряд достоинств при выполнении арифметических операций и переводе чисел из одной системы счисления в другую.
Особенностью взвешенных ДДК, имеющих только положительные веса, кроме кодов «8, 4, 2, 1», является отсутствие однозначного представления десятич- ных цифр. Любой двоичный код здесь соответствует одной десятичной цифре, но десятичная цифра может быть представлена несколькими двоичными кодами. Например, в коде «2, 4, 2, 1» цифра 2 может быть представлена как 1000 или как 0010. Причиной тому служит неоднозначность решения уравнений (3) отно-сительнопеременных xh, xh -1 ,..., х 1. Для выполнения условия единственности кодирования уславливаются считать «запрещенными» некоторые, хотя и правиль- ные, двоичные коды десятичных цифр. Однозначностьпредставления десятичныхцифр, состоящая в том, что каждой такой цифре соответствует только одна из шестнадцати возможных комбинаций двоичных цифр, обеспечивается в коде «8, 4, 2, 1». Кроме того, требование однозначности представления десятичных цифр мо- жет быть выполнено введением отрицательных весов. В табл. 4 представлены все группы кодов, удовлетворяющие требованию однозначности.
Таблица 4
| № п/п | Веса разрядов | № п/п | Веса разрядов |
| 8 4 2 1 | 8 5 –4 2 | ||
| 8 4 2-1 | 8 –5 4 2 | ||
| 8 4 –2 1 | 8 5 –4 -2 | ||
| 8 –4 2 1 | 8 6 –4 1 | ||
| 8 –4 –2 1 | 8 –6 4 1 | ||
| 8 –4 2 -1 | 8 6 –4 -1 | ||
| 8 4 –3 2 | 8 –6 4 3 | ||
| 8 4 3 -2 | 8 7 –4 -2 | ||
| 8 –4 3 2 | 7 6 –5 3 | ||
| 8 4 –3 -2 | 7 –6 5 3 | ||
| 8 –4 3 -2 | -7 6 5 3 |
Для представления десятичных цифр могут быть использованы и невзве- шенные ДДК. Код «с избытком 3» (табл. 3) обладает свойством дополнительнос- ти. Этот код удобен для выполнения операции алгебраического сложения. Для за- писи десятичных цифр в коде «с избытком 3» необходимо каждую двоичную тет- раду этой цифры в коде «8, 4, 2, 1» сложить с двоичным кодом цифры 3.
Код «8, 4, 2, 1» и коды с избытком (построенные по аналогии с кодом «с избытком 3») обладают свойством аддитивности, которое заключается в том, что код суммы двух десятичных цифр равен двоичной сумме кодов этих цифр или отличается от нее на некоторую константу. Это свойство позволяет свести операции десятичной арифметики в таких кодах к выполнению операций по пра- вилам двоичной арифметики.
Примерами ДДК, в которых каждая десятичная цифра кодируется пятью двоичными разрядами, являются коды «3 а + 2» и «2 из 5» (табл. 3). Первый код обладает свойством дополнительности и может быть получен путем записи в дво-ичной системе с естественным порядком весов числа 3 а + 2, где а – заданная десятичная цифра. В коде «2 из 5» каждая десятичная цифра изображается пятью двоичными разрядами, из которых только два содержат единицы. Можно считать, что код «2 из 5» получается из кода «7, 4, 2, 1» путем добавления справа дополнительного разряда с весом 0. В этот разряд записывается такая двоичная цифра, чтобы общее число единиц было равно двум (за исключением кода деся- тичного нуля). Коды «3 а + 2» и «2 из 5» используются для передачи информации, так как они позволяют обнаруживать наиболее вероятные ошибки.
В ВТ находит применение также двоично-пятеричная система счисления. В такой системе основание нечетных разрядов в записи числа равно 5, а основа- ние четных разрядов равно 2. Очевидно, что такую систему можно рассматри- вать как десятичную, цифры которой кодируются одной пятеричной и одной двоичной цифрами. Двоичная цифра (0 или 1) показывает, сколько пятерок вхо- дит в данную десятичную цифру, а пятеричная цифра (0, 1, 2, 3, 4) дает допол- нительное количество единиц. Например, десятичное число 791, 127 может быть записано в двоично-пятеричной системе с непосредственным представлением цифр в виде 12 14 01, 01 02 12.
В коде «2 из 7», который также называют двоично-пятеричным кодом, для представления десятичной цифры используется семь двоичных разрядов. Десятич- ные числа, записанные в этом коде, можно рассматривать как числа, представлен- ные в смешанной двоично-пятеричной системе счисления с кодированным пред-ставлением цифр. Пятеричные цифры кодируются пятью младшими разрядами, а двоичные – двумя старшими, причем в каждой группе разрядов должна быть запи- сана только одна единица. Этот код можно рассматривать как взвешенный код «5043210». Код «2 из 7» также, как и коды « 3 а + 2» и «2 из 5», позволяет обна- руживать наиболее вероятные ошибки при передаче информации. Кроме того, ко- ды «2 из 5» и «2 из 7» обеспечивают в ЭВМ с импульсным представлением информации постоянное и при этом минимальное потребление тока, так как любая десятичная цифра в этих кодах представляется комбинацией разрядов, содержа- щей только две единицы.
Представленный в табл. 3 рефлексный код обладает тем свойством, что двум соседним десятичным цифрам соответствуют кодовые комбинации, отличаю-щиеся друг от друга. только в одном двоичном разряде. Это свойство эффективно используется при преобразовании величины углового и линейного перемещения в цифровой эквивалент. Код, обозначенный в табл. 3 как «w, x, у, r», обладает сле-дующим свойством. Для любой десятичной цифры комбинация z, w, х, у дает млад- ший разряд произведения этой цифры на 3, комбинация х, у, г, w – младший разряд произведения цифры на 7, а комбинация у, г, w, x – младший разряд произведения на 9. Таким образом, младший разряд произведения десятичной цифры на 3, 7 и 9 может быть получен круговой перестановкой двоичных цифр.
Из числа других двоично-кодированных систем в ВТ нашли применение системы с основанием k = 2 r, в частности восьмеричная и шестнадцатиричная. Эти системы используются при составлении программ для более короткой и удобной записи двоичных представлений команд, так как в этом случае нет необходимос- ти выполнять специальные операции для перевода чисел в двоичную систему. В табл. 5 приведены изображения некоторых целых и дробных чисел в позицион- ных системах с основаниями k = 2, 8, 10, 16. Здесь шесть старших цифр шест- надцатиричной системы обозначены буквами А, В, С, D, Е, F (соответствуют десятичным числам 10, 11, 12, 13, 14, 15).
Таблица 5.
| k | k | ||||||
| 0,1 | 0,0001… | 0,06… | 0,19… | ||||
| 0,2 | 0,0011… | 0,14… | 0,33… | ||||
| 0,3 | 0,0100… | 0,23… | 0,4C… | ||||
| 0,4 | 0,0110… | 0,31… | 0,66… | ||||
| 0,5 | 0,1000 | 0,4 | 0,8 | ||||
| 0,6 | 0,1001… | 0,46… | 0,99… | ||||
| 0,7 | 0,1011… | 0,54… | 0,B3… | ||||
| 0,8 | 0,1101… | 0,63… | 0,CC… | ||||
| 0,9 | 0,1110… | 0,71… | 0,E6… | ||||
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F | |||||||
В современных ЭВМ, обрабатывающих не только числовую информацию, но и текстовую (алфавитно-цифровую), отдельные символы чаще всего представ- ляют словами длиной в один байт. Так как один байт равен двум двоичным тетра- дам, то в ЭВМ с байтовым представлением информации можно записывать две десятичные цифры в один байт. Вместе с тем можно записывать в каждый байт и по одной десятичной цифре, используя остальные четыре разряда байта для за- писи знаков и вспомогательных символов. Например, в ЭВМ Единой Системы (ЕС ЭВМ) реализованы обе возможности, причем первая используется для обра- ботки числовой десятичной информации, а вторая – для обработки текстовой ин-формации.
В специализированных цифровых устройствах находят применение системы счисления с иррациональным основанием, к которым относятся так называемые Р -коды Фибоначчи и коды «золотой» Р -пропорции. При этом Р -кодом Фибоначчи называется представление числа X в виде
|
где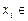 
{0, 1} — двоичная цифра в i -м разряде, 
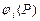— вес i -ro разряда, опре-деляемый как
Если Р = 0, то Р -код Фибоначчи совпадает с представлением чисел в дво- ичной канонической системе счисления. В случае Р = 1 код Фибоначчи соответ- ствует системе счисления с искусственным порядком весов, а именно: 1, 1, 2, 3, 5, 8, 13, 21, 34,... В этой последовательности любой вес равен сумме двух соседних младших весов. Если Р = 2, то последовательность весов Р -кода Фибоначчи име- ет вид 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28,.... При 
подобная последова- тельность состоит из Р единиц, после которых следует натуральный ряд чисел. Как и в других системах с искусственным порядком весов, представление чисел в Р -кодах Фибоначчи не является однозначным. К числу основных достоинств кодов Фибоначчи следует отнести повышение быстродействия устройств обработки ин-формации и удобство организации контроля правильности их функционирования.
Кодом «золотой» Р -пропорции называется представление числа X в виде
где xi — двоичная цифра в i -м разряде, 
— вес i- го разряда, причем = 
+ 
.
Приведенное представление задает бесконечное число способов нумерации действительных чисел, так как каждому Р соответствует свой способ нумерации. Веса разрядов в таком представлении связаны с весами разрядов в Р -кодах Фибо- наччи следующим соотношением:
Отсюда при Р = 0 следует 
(0) = 2, т. е. код «золотой» Р -пропорции в этом случае соответствует двоичной позиционной системе счисления. При Р > 0 значение (Р) является иррациональным числом. В частности, для Р = 1
Подобно Р -кодам Фибоначчи особенностью кодов «золотой» Р -пропорции является неоднозначность представления действительных чисел (за исключением нуля). Кроме того, при Р > 0 понятия целого и дробного числа не совпадают с общепринятыми понятиями. Например, целое число 3 в коде «золотой» 1-пропор- ции изображается как 100,01, а иррациональное число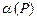 
при любом Р > 0 изображается как и основание системы счисления в канонической двоичной сис- теме, т. е. 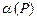= 10.
Число 
было известно еще древним грекам из реше- ния задачи о делении отрезка в среднем и крайнем отношениях. В средние века такое пропорциональное отношение было названо «золотым». Этим и объясняется происхождение названия кодов «золотой» Р -пропорции.
