Прямой, обратный и дополнительный код

Алгоритмы выполнения операций сложения и вычитания в по­зиционной системе счисления с основанием k устанавливаются аналогично соответствующим алгоритмам в обычной десятичной систе­ме. Результаты выполнения операций сло-жения и вычитания цифр х и у в одном разряде представляются двумя цифрами: цифрой s результата соответствующей операции в данном разряде и цифрой r переноса (заема) в старшем разряде. Правила формирования цифр s и r при любом k для всех указанных операций можно записать так:

а)для сложения

б) для вычитания

 

Для правильного выполнения арифметических операций над числами, у которых знаки закодированы цифрами, используются спе­циальные способы пред-ставления чисел: прямой, обратный и до­полнительный коды.

Представление числа X в прямом коде определяется выраже­нием

 

(6)

 

 

т. е. прямые коды чисел + X и —X отличаются только знаковыми разрядами. Из (6) видно, что нуль в прямом коде может быть представлен двояко: положительный нуль +0 = 0_пр = 0.00... 0,00... 0 и отрицательный нуль – 0 = 0_пр = . 00... 0,00... 0.

Используется прямой код в ЭВМ для ввода и вывода информации, а также для представления чисел в запоминающих устройствах. Сложение чисел с одина- ковыми знаками в прямом коде выполняется в соответствии с приведенными вы- ше правилами и не вызывает за­труднений. Наличие цифры переноса r _слож = 1 при сложении стар­ших разрядов n -разрядных чисел X и Y, представленных в форме (1), свидетельствует о том, что

т. е. для представления результата операции требуется болъше, чем п разрядов (X _max= k ^s — k ^{- m} – максимальное число, которое может быть представлено п раз- рядами в форме (1)). В этом слу­чае говорят, что происходит переполнение разряд- ной сетки. Одна­ко складывать числа с разными знаками (т. е. выполнять алгебраи­ческое сложение) в прямых кодах неудобно, так как в составе ЭВМ в этом случае должно быть специальное оборудование для вычита­ния чисел (вычитатель) и оп-ределения знака разности.

Операцию алгебраического сложения чисел можно свести к опе­рации сложе-ния при использовании обратных кодов. Способ пред­ставления числа X, записан- ного в форме (1), в обратном коде оп­ределяется выражением

 

(7)

 

Сравнивая (6) и (7), легко заметить, что обратный код по­ложительного числа совпадает с его прямым кодом.

Так как при k =2

то для получения обратного кода отрицательного числа в двоичной системе счис- ления необходимо в знаковом разряде записать 1, а в остальных разрядах едини- цы заменить нулями и нули единицами. Аналогичным образом переходят от об- ратного кода отрицательного числа к прямому коду. Для получения обратного ко- да отрицатель­ных чисел в k -йсистеме (k > 2) необходимо в знаковый разряд за- ­писать цифру k – 1, а остальные цифры заменить их дополнениями до k – 1. На- пример, в десятичной системе заменяют 9 на 0, 8 на 1 и т. д. В отличие от пря- мого кода в обратном коде нельзя отбрасы­вать нули после знакового разряда в целой части, смещая знаковый разряд вправо, и нули в конце дробной части от-рицательных чисел, но можно отбрасывать записанные на этих местах цифры k – 1. Нуль в обратном коде так же, как и в прямом коде, имеет два изображения. Если числа X и Y положительные, то их сложе­ние не отличается от сложения в прямом коде. Когда же одно из чисел (например, Y) отрицательное и представлено обрат- ным кодом, то без учета знаковых разрядов можно записать, что

(8)

Дальнейшее выполнение операции зависит от знака разности Δ = | X | - | Y |. При Δ < 0 выражение (8) можно записать так: Z = k ^s+1 - k ^{- m} - Δ < Х _max. В этом случае перенос при сложении старших разрядов равен нулю, а сам результат будет представлен обратным кодом. Для образования кода знака результата дос- таточ­но сложить коды знаков чисел. Это осуществляется одновременно со сложе- нием кодов чисел.

При Δ > 0 получим Z = k ^s+1- k ^-m + Δ > Х _max.

В этом случае возникает единичный перенос при сложении старших раз- рядов, имеющий вес k ^s+1, а в п числовых разрядах будет записано число Δ – k ^-m. Знаковые разряды чисел суммируются с учетом переноса с весом k ^s+1. Образую- щейся при этом единице пе­реноса можно приписать вес k ^-m и сложить ее с чис- лом Δ – k ^–m. В этом случае будет получена правильная сумма чисел X и Y. Пе- ренос, возникающий при сложении знаковых разрядов и прибав­ляемый к млад- шему разряду суммы чисел, называется циклическим переносом.

Если числа X и Y отрицательные, то (без учета знаковых разря­дов)

 

Первое число k ^s+1в полученном выражении соответствует пере­носу из старшего разряда. Поэтому в числовых разрядах будет на­ходиться число Z = k ^s+1 –– k ^-m – (| X | + | Y |) – k ^-m, которое по­сле прибавления единицы циклического пе- реноса, образующейся при сложении знаковых разрядов, будет представлять собой сумму чисел X и Y, записанную в обратном коде.

При использовании обратных кодов для алгебраического сло­жения положи-тельная сумма всегда представлена прямым кодом, а отрицательная сумма – обрат- ным кодом. Недостатком способа алгебраического сложения с использованием об- ратных кодов явля­ется наличие циклического переноса, для учета которого в ЭВМ не­обходимы дополнительные затраты времени. От этого недостатка свободен спо- соб выполнения алгебраического сложения в допол­нительных кодах.

Дополнительный код числа X образуется в соответствии со сле­дующим правилом

 

(9)

 

Представление положительного числа в дополнительном коде совпадает с его прямым кодом. Из сравнения вторых строк выражений (7) и (9) следует, что дополнительный код отрицательного числа отличается от обратного кода того же числа на величину k ^-m. На этом основано правило формирования дополнительного кода отрицательного числа – достаточно получить обратный код числа и приба- вить 1 в его младший разряд. При k = 2 тот же результат может быть получен, если в прямом коде отрицательного числа оста­вить без изменения крайние справа нули и первую единицу за ними, а все цифры левее этой единицы (кроме знаково- го разряда) по­менять на обратные. Преобразование дополнительного кода отрица-тельного числа в прямой код может быть осуществлено либо обратным путем (т.е. вычитанием 1 в младшем разряде и последу­ющим преобразованием обратного кода), либо путем формирования дополнительного кода от дополнительного. Оба пути при-водят к одинаковому результату. Нуль, в отличие от прямого и обратного кодов, в дополнительном коде имеет единственное представление 0_доп = 0.000... 0,00... 0.

Сложение положительных чисел X и Y в дополнительном коде выполняет- ся так же, как и в прямом и обратном кодах. Если число Y отрицательное, то без учета знаковых разрядов получим

 

 

При Δ > 0 число k ^s+1соответствует переносу при сложении старших раз- рядов, который учитывается при сложении знаковых разрядов. При Δ< 0 перенос из старших разрядов в знаковые от­сутствует, а отрицательный результат будет представлен допол­нительным кодом.

Сложение числовых разрядов отрицательных чисел X и Y вдополнительном коде дает следующий результат:

Следовательно, при сложении старших разрядов будет возни­кать перенос (о чем свидетельствует первое число k ^s+1), который прибавляется к сумме знаковых разрядов. Перенос из зна­ковых разрядов при сложении не учитывается (теряется). Отри­цательный результат в этом случае будет представлен дополнительным ко-дом.

Таким образом, при выполнении операции сложения чисел с одинаковыми знаками может произойти переполнение раз­рядной сетки, когда для представления результата требуется боль­шее количество разрядов, чем для представления чисел. Поскольку знаковые разряды складываются с учетом переноса из старшего разряда, то это может привести к неправильному результату. Не­зависимо от кода для пред-ставления отрицательных чисел (обрат­ный или дополнительный) переполнение разрядной сетки происхо­дит всегда, если только при сложении положительных чи- сел возникает перенос в знаковый разряд, а при сложении отрицательных чисел такой перенос отсутствует.

Уменьшить вероятность переполнения разрядной сетки можно путем введе- ния масштабных коэффициентов, на которые умножа­ются все исходные данные пе- ред решением задачи. Однако для пол­ного исключения переполнения необходимо оценивать возможные значения результата после каждой операции, что практически не­выполнимо ввиду большого числа операций. Поэтому в ЭВМ при­нимаются спе-циальные меры для обнаружения переполнения разряд­ной сетки. Наиболее широко для этой цели используются два способа.

При обнаружении переполнения по первому способу учитывает­ся то обсто-ятельство, что переполнение может появиться только при сложении чисел с одина-ковыми знаками. В этом случае о пере­полнении будет свидетельствовать несовпаде- ние знака слагаемых и знака суммы. Недостатком этого способа является необхо-димость реализации двукратного сравнения знаков чисел и их запоминания до кон- ца операции.

Сущность второго способа состоит в использовании так называ­емых моди-фицированных прямого, обратного и дополнительного кодов. Особенностью этих кодов является наличие двух знаковых разрядов, в которых знак числа представля- ется двумя одинаковы­ми цифрами. Появление в знаковых разрядах модифициро- ванного кода, обрабатываемых так же, как и числовые разряды, различных цифр (например, 01 при сложении положительных двоичных чисел и 10 при сложении отрицательных двоичных чисел) свидетельствует о переполнении разрядной сетки. Циклический перенос в случае модифицированного обратного кода возникает при сложении вторых (крайних слева) знаковых разрядов. Этот способ обнаружения пере­полнения получил наибольшее распространение в ЭВМ.

В СОК, как и в смещенных системах счисления, знаки чисел ука­зываются в специальном знаковом разряде, а кодируются они так же, как и в двоичной системе счисления. Для выполнения опе­раций алгебраического сложения чисел в СОК чаще всего исполь­зуются дополнения отрицательных чисел, являющиеся ана-логами дополнительного кода в позиционных системах. При этом дополне­нием отрицательного числа X = (Х ₁, Х ₂, ..., Х_т) в СОК называется величина

,

где , P_i – основания СОК (i = ).

Поскольку N в СОК можно пред­­ставить как

N = (0, 0, …,0) = (P ₁, P ₂, …, P_m),

а 0 ≤ X ≤ N, то компоненты X_g по каждому модулю P_i могут быть определены по формуле

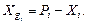
Если один из модулей P_i равен 2 (например, Р ₁ = 2 ), то исполь­зование дополнений отрицательных чисел означает, что в качестве нуля в СОК принимается величина , диапазон изменения чисел расположен симметрично относительно Q,поло­жительные числа X должны быть представлены в виде ,а отрицательные — в виде . Такое представ­ление чисел в СОК называется искусственной формой. Если ни один из модулей Р_i не равен 2, то принимают и называют такое представление обобщенной искусст-венной формой.