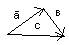
Правило параллелограмма
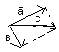
Если вектора заданы в прямоугольной системе координат ā (а1,а2), в-(в1,в2), то чтобы найти сумму надо сложить с-(а1+в1;а2+в2)
2) Арифметические векторы пространства R
Арифметическим вектором называется упорядоченная совокупность n чисел.
Обозначается x = (x 1, x 2,..., x n);
числа x 1, x 2, ...,xn называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:
для любых x = (x 1, x 2,..., x n), y = (y 1, y 2,..., y n) и любого числа α справедливо:
x + y = (x 1+ y 1, x 2 + y 2,..., x n + yn);αx = (αx 1, αx 2,..., α x n).
Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.
Вектор θ = (0, 0,..., 0) называется нулевым вектором Rn,
а вектор −x = (−x 1, −x 2,..., −x n) — противоположным вектором для вектора x в Rn.
3)Скалярное произведение двух векторов в пространстве определяется аналогично случаю на плоскости:
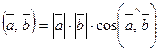 .
.
Формула скалярного квадрата:
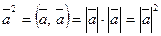 .
.
Справедлива формула, связывающая скалярное произведение векторов и проекции этих векторов:
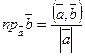 . (1)
. (1)
4)Линейная зависимость векторов. Действия над векторами в координатной форме
Векторы 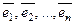 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство
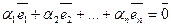
справедливо тогда и только тогда, когда 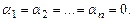 В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы
В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы 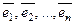 были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
5) Ортогональность векторов
Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот.
6)Базис пространства R
Базис векторного пространства и его размерности.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.
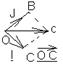
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у называются координатами вектора ОС в данном базисе
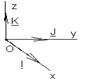
(НЕОБЯЗАТЕЛЬНО)Упорядоченная тройка 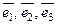 ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор
ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор 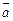 пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде
пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде
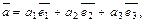
где 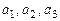 – координаты вектора
– координаты вектора 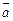 в базисе
в базисе 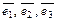 (записывают:
(записывают: 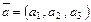 ).
).
В пространстве линейная независимость векторов равносильна их некомпланарности, т.е. любые три некомпланарных вектора, взятые в определенном порядке, образуют базис.
Пусть задана тройка 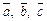 некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора
некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора 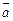 до направления вектора
до направления вектора 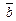 , наблюдаемый с конца вектора
, наблюдаемый с конца вектора 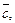 совершается против часовой стрелки, то тройка векторов
совершается против часовой стрелки, то тройка векторов 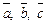 называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.
называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.
В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой. Если добавить, кроме того, условие нормированности базисных векторов (т.е. их единичную длину), то такой базис называют ортонормированным и обозначают 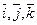 :
: 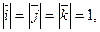
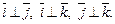 Прямоугольные декартовы координаты вектора
Прямоугольные декартовы координаты вектора 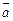 является его проекциями на вектора
является его проекциями на вектора 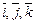 соответственно.
соответственно.
Если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O (0, 0, 0) и базисом 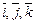 , то соответствующий радиус-вектор
, то соответствующий радиус-вектор
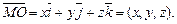
Если 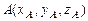 и
и 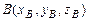 , то
, то
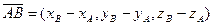 .
.
Линейные операции для векторов 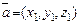 и
и 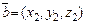 в координатной форме и их скалярное произведение вычисляются по формулам:
в координатной форме и их скалярное произведение вычисляются по формулам:
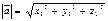 ; (4)
; (4)
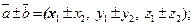 (5)
(5)
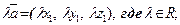 (6)
(6)
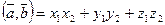 ; (7)
; (7)
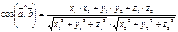 . (8)
. (8)
Направляющими косинусами вектора 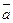 называются величины
называются величины 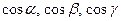 , где
, где 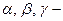 углы, которые образует вектор
углы, которые образует вектор 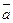 соответственно с осями
соответственно с осями 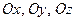 . Их вычисляют по формулам:
. Их вычисляют по формулам:
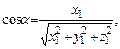
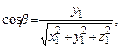 (9)
(9)
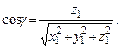
Если 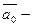 единичный вектор, то
единичный вектор, то 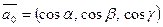 .
.
7) Основные сведения о матрицах
Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Горизонтальные ряды такой таблицы называются строками матрицы, а вертикальные – ее столбцами. Матрицы обозначают A, B, C, X …. Запись aij используется для указания местоположения элемента матрицы (i – номер строки, j – номер столбца). Числовую матрицу размера 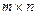 (то есть состоящую из m строк и n столбцов чисел) в общем случае записывают в виде:
(то есть состоящую из m строк и n столбцов чисел) в общем случае записывают в виде:
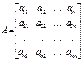
или в более компактной форме 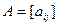 ,
, 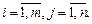 .
.
Eё обозначают также 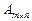 .
.
Если 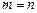 , то матрицу называют квадратной и обычно обозначают An. Элементы aii, (
, то матрицу называют квадратной и обычно обозначают An. Элементы aii, (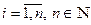 ) такой матрицы образуют ее главную диагональ.
) такой матрицы образуют ее главную диагональ.
Квадратная матрица вида 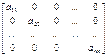 , (1)
, (1)
где 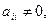
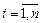 , называется диагональной. Если
, называется диагональной. Если 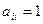 для любого
для любого 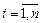 , то матрица (1) называется единичной и обозначается En.
, то матрица (1) называется единичной и обозначается En.
Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.
Две матрицы одинакового размера
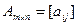 и
и 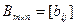 (2)
(2)
называются равными, если 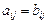 для всех
для всех 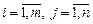 .
.
8) Операции над матрицами (сложение, вычисление, умножение)
Суммой матриц (2) называется матрица A + B размера m×n, состоящая из элементов 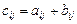 , где
, где 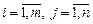 .
.
Произведением матрицы Am×n на число α называется матрица 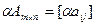 .
.
Разностью матриц (2) называется матрица A–B = A+ (–1)B.
Свойства операций сложения матриц и умножения на число:
1) 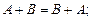
2) 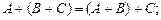
3) 0·A= О;
4) 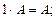
5) 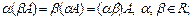
6) 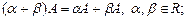
7) 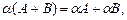
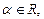 A и B – матрицы одинакового размера.
A и B – матрицы одинакового размера.
Для матриц A и B может быть введена операция умножения A · B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.
Произведением матрицы Al×m на матрицу Bm×n называется матрица 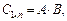 элементы которой
элементы которой
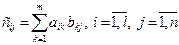 .
.
Для получения элемента 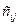 матрицы – произведения умножают последовательно каждый элемент
матрицы – произведения умножают последовательно каждый элемент 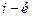 строки матрицы А на каждый элемент j-го столбца матрицы В и находят сумму этих произведений.
строки матрицы А на каждый элемент j-го столбца матрицы В и находят сумму этих произведений.
Свойства операции умножения матриц:
1) 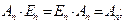
2) 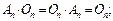
3) 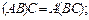
4) 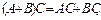
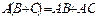
В общем случае из существования AB не следует существование BA. Даже если оба эти произведения определены, они не всегда равны. Матрицы, для которых 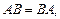 называются коммутативными.
называются коммутативными.
Пусть A – квадратная матрица. Тогда k -я степень (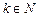 ) матрицы A определяется равенством
) матрицы A определяется равенством 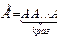 . По определению принимают
. По определению принимают 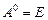 при условии
при условии 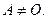
Элементарными преобразованиями над строками матрицы A называют следующие операции:
1) перестановку строк;
2) умножение строки на ненулевое число;
3) прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.
Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.
9) Транспонирование матрицы,
возведение в степень - Матрица AT, полученная из матрицы A заменой столбцов строками с теми же номерами, называется транспонированной к матрице A, то есть 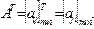
Свойства операции транспонирования матриц:
1) 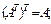
2) 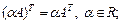
3) 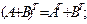
4) 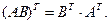
Если для квадратной матрицы A выполняется соотношение 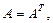 то матрица A называется симметрической матрицей, а если
то матрица A называется симметрической матрицей, а если 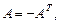 – то кососимметрической. Возведение в степень матрицы осуществляется произведением матрицы на себя в количестве указанной порядком степени
– то кососимметрической. Возведение в степень матрицы осуществляется произведением матрицы на себя в количестве указанной порядком степени
10) Определители. Основная теорема об определителях
Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем (или детерминантом) матрицы A и обозначается |A|, или det A, или Δ(A). Порядок матрицы A является и порядком ее определителя. Определители порядка 1-3 определяются, соответственно, равенствами:
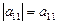 ,
,
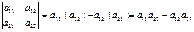 , (3)
, (3)
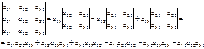 .
.
Основные методы вычисления определителей.
1. Для определителей 3-го порядка удобно использовать правило треугольников, которое схематично можно изобразить следующим образом:
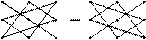
Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.
2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):
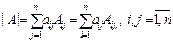 .
.
3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, были нулями, затем вычисляют определитель разложением по этой строке (столбцу).
4. Метод приведения к треугольному или диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.
Минором Mij элемента ai j, 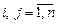 , называется определитель (n -1)-го порядка, который состоит из элементов матрицы, полученной из данной после «вычеркивания» i - той строки и j -того столбца.
, называется определитель (n -1)-го порядка, который состоит из элементов матрицы, полученной из данной после «вычеркивания» i - той строки и j -того столбца.
Алгебраическим дополнением элемента a ij называется число Аij =(-1) i+j M ij. Определитель порядка n, где 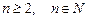
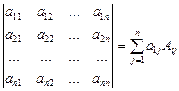 , определяется как число.
, определяется как число.
Последнее равенство называют разложением определителя по элементам первой строки. Оно есть обобщение равенств (3).
11)Свойства определителей:
1) 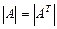 ;
;
2) 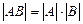 ;
;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) перестановка двух строк (столбцов) меняет знак определителя на противоположный;
5) |A|=0, если выполняется одно из следующих условий:
· в определителе есть нулевая строка (нулевой столбец),
· в определителе есть пропорциональные строки (столбцы),
· в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);
6) если к элементам одной строки (столбца) определителя прибавить линейную комбинацию соответствующих элементов других строк (столбцов), то значение определителя не изменится.
12) Обратная матрица
Квадратная матрица B, удовлетворяющая совместно с заданной матрицей A того же порядка равенствам 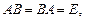 называется обратной матрицей к A и обозначается A –1. Обратная матрица A –1 существует при условии, что A – невырожденная матрица, т. е.
называется обратной матрицей к A и обозначается A –1. Обратная матрица A –1 существует при условии, что A – невырожденная матрица, т. е. 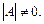
Обратную матрицу можно вычислить следующими способами.
1-й способ. Используют формулу
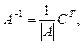 (4)
(4)
где С – матрица, составленная из алгебраических дополнений соответствующих элементов матрицы A.
13) Алгоритм вычисления обратной матрицы
1. Вычисляем определитель матрицы A. Если det A ≠ 0, то матрица A имеет обратную
2. Составляем матрицу из алгебраических дополнений элементов матрицы A
3. Находим транспонированную матрицу для матрицы, составленной из алгебраических дополнений
4. Разделив матрицу ˜AT на определитель, получаем искомую обратную матрицу
5. Проверяем, что A · A−1 = E, и записываем ответ
Аналогично вычисляется обратная матрица для невырожденной матрицы любого порядка
14) Ранг матрицы
Рангом матрицы A размера 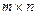 называется максимальный порядок
называется максимальный порядок 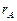 отличных от нуля ее миноров. При этом любой ненулевой минор порядка
отличных от нуля ее миноров. При этом любой ненулевой минор порядка 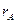 называется базисным минором матрицы A.
называется базисным минором матрицы A.
Основные методы нахождения ранга матрицы A.
Метод окаймляющих миноров
Если в матрице A найден ненулевой минор Mk порядка k, 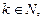 а все окаймляющие его миноры
а все окаймляющие его миноры 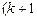 )-го порядка равны нулю, то ранг матрицы равен k (
)-го порядка равны нулю, то ранг матрицы равен k (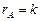 ).
).
Метод элементарных преобразований
Используя элементарные преобразования строк, матрицу приводят к трапециевидной или треугольной форме, далее ранг находят по определению.
Как частный случай последнего метода, может быть рассмотрен метод нулей и единиц: элементарными преобразованиями строк матрицу приводят к эквивалентной, состоящей или из нулевых строк и столбцов, или из строк и столбцов, в которых содержится ровно одна единица, а остальные элементы – нулевые. Количество единиц в такой матрице равно ее рангу.
15) Системы линейных уравнений с n неизвестными
Система линейных алгебраических уравнений (или линейная система) имеет вид:
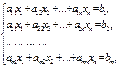
где aij и bj –заданные числа.
Систему (17) можно записать в матричной форме
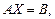 (8)
(8)
где А – матрица системы, состоящая из коэффициентов;
B – матрица-столбец свободных членов;
X – матрица-столбец неизвестных. е. 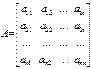 ,
, 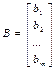 ,
, 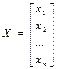 .
.
Решением системы (7) называется совокупность n чисел 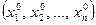 , которые после подстановки в уравнения системы вместо соответствующих неизвестных обращают каждое уравнение системы в верное числовое тождество.
, которые после подстановки в уравнения системы вместо соответствующих неизвестных обращают каждое уравнение системы в верное числовое тождество.
Система (7) называется совместной, если у нее существует хотя бы одно решение, в противном случае она называется несовместной. Совместная система (7) называется определенной, если она имеет одно решение и неопределенной, если более одного решения. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.
Определителем системы (9) называется определитель матрицы этой системы (состоящий из коэффициентов: 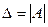 , Если
, Если 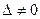 то система называется невырожденной; если
то система называется невырожденной; если 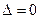 - вырожденной.
- вырожденной.
Методы решения невырожденных систем используются для решения линейных систем (9), состоящих из n уравнений с n неизвестными из которых 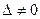 .
.
16) Метод обратной матрицы состоит в решении матричного уравнения 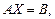
где А – матрица системы, состоящая из коэффициентов;
B – матрица-столбец свободных членов;
X – матрица-столбец неизвестных. е. 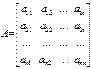 ,
, 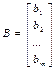 ,
, 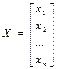 по формуле
по формуле
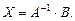
17) Метод Крамера: для нахождения неизвестных необходимо использовать формулы
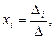
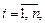 (11)
(11)
где 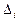 – определитель, получаемый из определителя
– определитель, получаемый из определителя 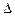 системы
системы 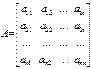 ,
, 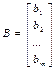 ,
, 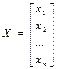 . заменой i -го столбца столбцом свободных членов.
. заменой i -го столбца столбцом свободных членов.
Формулы (11) называются формулами Крамера.
Решение произвольных линейных систем
18) Метод Гаусса
используется в общем случае для систем вида 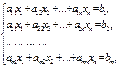 (7)
(7)
(вырожденных и невырожденных). С помощью элементарных преобразований над строками расширенную матрицу системы (7) приводят к виду:
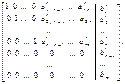
Соответствующая ей система, равносильная (7), примет вид:
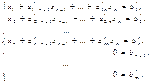 (12)
(12)
Если хотя бы одно из чисел br + 1, … bm отлично от нуля, то система (11), а значит, и исходная система (7) несовместны.
Если br + 1 = … = bm = 0, то система (11) позволяет получить явное выражение для базисных неизвестных x 1, …, xr через свободные неизвестные xr + 1, …, xn. Получаем бесконечное множество решений.
Если r = n, то свободные неизвестные отсутствуют, а значит, системы (11) и (7) имеют единственное решение. На практике обычно обходятся приведением матрицы системы (7) к треугольной или трапециевидной форме, после чего значения базисных переменных ищутся в обратном порядке.
19) Однородные системы уравнений
Однородной системой m линейных алгебраических уравнений для n неизвестных называется система уравнений
вида 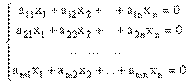 (1) или в матричном виде
(1) или в матричном виде 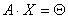 (2)
(2)
где А -заданная матрица из коэффициентов размером mxn,
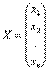 - столбец n неизвестных,
- столбец n неизвестных,  - нулевой столбец высоты m.
- нулевой столбец высоты m.
Однородная система всегда совместна (расширенная матрица совпадает с А) и имеет очевидные решения: х1 = х2 = … = хn = 0.
Это решение называется нулевым или тривиальным. Всякое другое решение, если оно есть, называется нетривиальным.
20) Расстояние между точками, площадь треугольника
Расстояние между двумя точками на плоскости рассчитывается по следующей формуле: 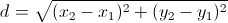
где x1 и y1 координаты первой точки, а x2 и y2 координаты второй точки.
Расстояние между двумя точками в трехмерном пространстве расчитывается по следующей формуле: 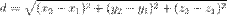
где x1, y1 и z1 координаты первой точки, а x2, y2 и z2 координаты второй точки.
Площадь треугольника:
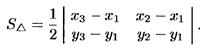 - S треуг
- S треуг
21)Деление отрезка в данном отношении
Координаты точки C, делящей отрезок AB в отношении 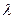 ,
, 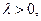 можно найти по формулам:
можно найти по формулам:
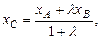
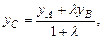
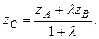
22) Полярные координаты
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Пару полярных координат r и φ можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
x = rcos φ,
y = rsin φ,
в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:
r2 = y2 + x2 (по теореме Пифагора).
23) Уравнение прямой с угловым коэффициентом

24) Уравнение прямой проходящей, через данную точку в заданном направлении..
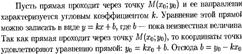

Уравнение прямой, проходящей через две данные точки

25) Угол между прямыми. Условие параллельности и перпендикулярности прямых.

26) Общее уравнение прямой. Уравнение прямой в отрезках на осях.
Общее уравнение прямой

Уравнение прямой в отрезках на осях

27) Нормальное уравнение прямой. Расстояние от точки до прямой.
Нормальное уравнение прямой

Расстояние от точки до прямой


28) Окружность

2 9) Эллипс

Эксцентриситет 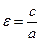 величина, характеризующая меру сжатия эллипса,
величина, характеризующая меру сжатия эллипса, 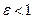 Директрисы
Директрисы 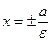
30) Гипербола

Гипербола – ГМТ М на плоскости, модуль расстояний от которых до двух фиксированных точек 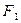 и
и 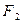 есть постоянная величина 2а, меньшая расстояния между фокусами 2с:
есть постоянная величина 2а, меньшая расстояния между фокусами 2с:
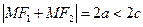
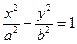
Эксцентриситет 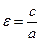 для гиперболы
для гиперболы 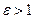
Директрисы 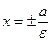
Прямая называется асимптотой гиперболы, если расстояние от точки М(х,у) гиперболы до этой прямой стремится к 0 при х → ± бесконечность.
Асимптоты гиперболы 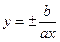
Отношение расстояния r от точки гиперболы до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету: 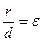
31) Директрисы эллипса и гиперболы.
Эллипс
Эксцентриситет 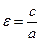 величина, характеризующая меру сжатия эллипса,
величина, характеризующая меру сжатия эллипса, 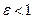
Директрисы 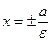
Отношение расстояния r от точки эллипса до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету: 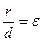
Гипербола
Эксцентриситет 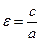 для гиперболы
для гиперболы 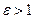
Директрисы 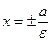
Прямая называется асимптотой гиперболы, если расстояние от точки М(х,у) гиперболы до этой прямой стремится к 0 при х → ± бесконечность.
Асимптоты гиперболы 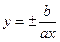
Отношение расстояния r от точки гиперболы до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету: 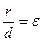
32) Парабола
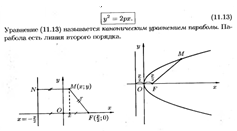

Парабола – множество точек плоскости, равноудалённых от фиксированной точки плоскости (фокуса) и фиксированной прямой плоскости (директрисы).
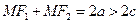
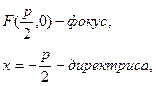
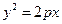 p-параметр параболы
p-параметр параболы
33) Общее уравнение плоскости
Плоскостью в пространстве называется множество всех точек М (х; у; z), координаты которых удовлетворяют уравнению
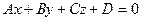 , (6.1)
, (6.1)
где А, В, С, D – заданные числа, причем А, В и С не равны нулю одновременно. Уравнение (6.1) называется общим уравнением плоскости.
Геометрический смысл коэффициентов А, В и С состоит в том, что вектор 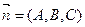 перпендикулярен плоскости, его называют нормальным вектором плоскости. Этот факт устанавливается так же, как и в случае общего уравнения прямой на плоскости.
перпендикулярен плоскости, его называют нормальным вектором плоскости. Этот факт устанавливается так же, как и в случае общего уравнения прямой на плоскости.
Из уравнения (6.1) следует, что если D = 0, то плоскость проходит через начало координат, так как координаты начала координат О (0;0;0) удовлетворяют уравнению 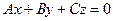 .
.
Пусть С =0. Тогда уравнение
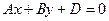 (6.2)
(6.2)
определяет плоскость, проходящую через прямую с этим уравнением в плоскости хОу и перпендикулярную этой плоскости. Какова бы ни была точка М (х; у; z), принадлежащая плоскости, ее координаты х, у удовлетворяют уравнению (6.2) независимо от того, какую она имеет третью координату z.
Если В = 0, С = 0, то уравнение
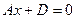 (А
(А 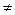 0) (6.3)
0) (6.3)
есть частный случай уравнения (6.2). Преобразовав его к виду 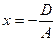 , заметим, что ему удовлетворяют точки, имеющие координату
, заметим, что ему удовлетворяют точки, имеющие координату 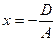 и произвольные координаты y и z, т.е. это плоскость, параллельная плоскости yOz или, что то же, перпендикулярная оси Ох.
и произвольные координаты y и z, т.е. это плоскость, параллельная плоскости yOz или, что то же, перпендикулярная оси Ох.
34)Угол между двумя плоскостями. Условие параллельности и перпендикулярности плоскостей.
Уравнение поверхности
Уравнение линии
Отметим без доказательства, что расстояние от точки 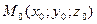 до плоскости, заданной уравнением
до плоскости, заданной уравнением 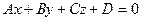 , находится по формуле
, находится по формуле
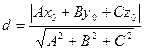 .
.
Поэтому координаты этих векторов пропорциональны, т.е.
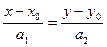
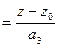 - (6.12)
- (6.12)
канонические уравнения прямой в пространстве, проходящей через точку 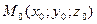 .
.
Угол между двумя плоскостями
Найдем теперь угол между плоскостями 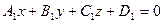 и
и 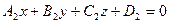 . Поскольку векторы
. Поскольку векторы 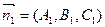 и
и 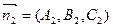 перпендикулярны данным плоскостям, то угол
перпендикулярны данным плоскостям, то угол 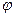 между ними равен двугранному углу между плоскостями. Поэтому
между ними равен двугранному углу между плоскостями. Поэтому
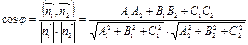 . (6.8)
. (6.8)
Если выражение в (6.8) положительное, то 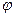 - острый угол, если отрицательное, то оно соответствует тупому двугранному углу
- острый угол, если отрицательное, то оно соответствует тупому двугранному углу 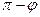 .
.
Условие параллельности и перпендикулярности двух плоскостей
Из формулы (6.8) получаем условие перпендикулярности двух плоскостей
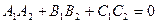 . (6.9)
. (6.9)
Условие параллельности двух плоскостей получается из условия коллинеарности векторов 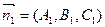 и
и 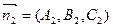 :
:
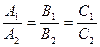 . (6.10)
. (6.10)
Если 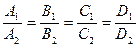 , то плоскости совпадают, так как их уравнения отличаются постоянным множителем.
, то плоскости совпадают, так как их уравнения отличаются постоянным множителем.
35) Нормальное уравнение плоскости. Расстояние от точки до плоскости.
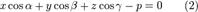
в векторной форме:
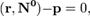
где 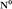 - единичный вектор,
- единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
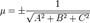
(знаки  и
и  противоположны).
противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние 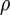 от точки
от точки 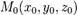 , до плоскости, заданной уравнением
, до плоскости, заданной уравнением 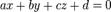 , вычисляется по формуле:
, вычисляется по формуле:
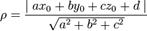
36) Общее уравнение прямой. Каноническое уравнение прямой.
Общее уравнение прямой
Если 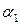 не параллельна
не параллельна 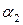 , то есть
, то есть 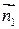 не коллинеарен
не коллинеарен 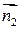 , то система уравнений
, то система уравнений
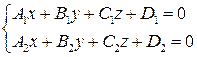 (3.42)
(3.42)
определяет прямую линию в пространстве.
| Уравнения (3.42) называются общими уравнениями прямой в пространстве. |
Каноническое уравнение прямой в пространстве
Отметим без доказательства, что расстояние от точки 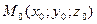 до плоскости, заданной уравнением
до плоскости, заданной уравнением 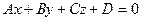 , находится по формуле
, находится по формуле
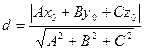 .
.
Поэтому координаты этих векторов пропорциональны, т.е.
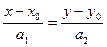
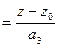 - (6.12)
- (6.12)
канонические уравнения прямой в пространстве, проходящей через точку 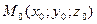 . Вектор
. Вектор 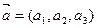 - направляющий векторпрямой.
- направляющий векторпрямой.
37) Параметрическое уравнение прямой
Обозначив общее значение дробей в уравнении 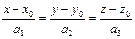 буквой t, т.е. положив
буквой t, т.е. положив 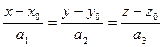 = t, получим
= t, получим
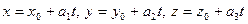 - (6.13)
- (6.13)
параметрические уравнения прямой в пространстве, проходящей через точку 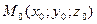 в направлении вектора
в направлении вектора 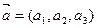 . Параметр
. Параметр 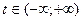 .
.
38) Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 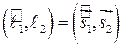 . Если
. Если 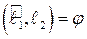 , то
, то
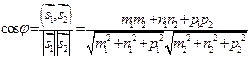 .
.
1) 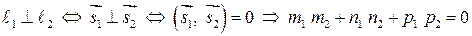 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
2) 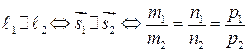 – условие параллельности прямых в пространстве.
– условие параллельности прямых в пространстве.
39) Расстояние от точки до прямой в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
Расстояние от точки до прямой в пространстве
Пусть прямая задана уравнением Ax+By+Cz+D=0
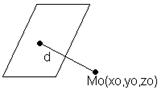

Условие параллельности и перпендикулярности прямых в пространстве.
Из формулы 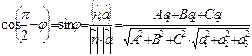 получаем условия параллельности
получаем условия параллельности
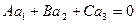
и перпендикулярности прямой и плоскости 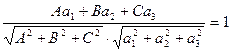
40) Угол между прямой и плоскостью
Пусть 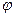 - угол между прямой
- угол между прямой 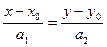
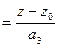 и плоскостью
и плоскостью 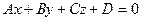 . Тогда угол между векторами
. Тогда угол между векторами 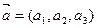 (направляющий вектор прямой) и
(направляющий вектор прямой) и 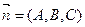 (нормальный вектор плоскости) равен
(нормальный вектор плоскости) равен 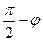 . Поэтому
. Поэтому
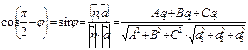
41)Числовая последовательность Если каждому числу n из ряда 1,2,3..n поставлено в соответсвие вещественное число xn, то множество вещественных чисел x1,x2…xn наз-ся числовой последовательностью, а xn -общим членом последов-ти. Сокращено обоз-ся {xn}. Последовательность задана, если указано условие получения любого ее элемента. Пусть даны послед-ти {xn},{yn}. Тогда суммой их называется последовательность {xn+yn}, а разностью – {xn-yn}. Произведением {xn} на число m назовем послед-ть {mxn} Произведение {xn} на {yn} есть {xnyn}, а частное – {xn/yn},где все члены {yn} ≠0. Последов-ть {xn} называется ограниченной сверху (снизу), если существует такое число M(m), что любой элемент xn этой последовательности удовлетворяет неравенству xn≤M (xn≥M). Последовательность xn наз-ся бесконечно большой, если для любого A>0 существует такой номер N, что при n>N выполняется неравенство: |xn|>A. Последовательность xn наз-ся бесконечно малой, если для любого ε>0 существует такой номер N, что при n>N выполняется неравенство: |xn|< ε. Если xn-бесконечно большая посл-ть и все ее члены отличны от нуля, то послед-ть {1/xn} является бесконечно малой. Число а называется пределом последовательности { xn }, если для любого положительного числа ε существует такой номер N, что при всех п > N выполняется неравенство 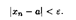
44)Сходимость последовательностей в пространстве Rn
Последовательность, имеющая предел, называется сходящейся. Если последовательность имеет своим пределом число а, то это записывается так: Последовательность, не имеющая предела, называется расходящейся
.45 Открытые и замкнутые множества в Rn. Предельные точки множества. Множество точек пространства Rn называется открытым, если вместе с каждой своей точкой оно содержит некоторую окрестность этой точки. Множество называется замкнутым, если оно включает все свои граничные (предельные) точки, т.е. точки, окрестности которых содержат точки как принадлежащие множеству, так и не принадлежащие ему. Пусть Х - множество в пространстве Rn. Точка р называется внутренней точкой множества Х, если существует шар В (р; r) (р- центр, r-радиус), все точки которого принадлежат множеству Х. Точка р называется внешней точкой по отношению к Х, если существует шар В (р;r),ни одна точка которого не принадлежит множеству Х. Точка р называется граничной, если она не является ни внутренней, ни внешней. Множество Х называется открытым, если каждая его точка является внутренней. Пусть Х-множество в пространстве Rn. Точка р0 называется предельной для множества Х, если в любой окрестности точки р0 имеются точки множества Х, отличные от р0. При этом точка р0 может как принадлежать, так и не принадлежать множеству Х. Точка р0 называется изолированной точкой, если существует такой шар В (р0;ε), в котором никаких точек из Х, кроме точки р0 не имеется
46. Число е. Задача на вычисление сложных процентов.
Рассмотрим последовательность { хп }, общий член которой выражается формулой 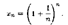 В курсе математического анализа доказывается, что эта последовательность монотонно возрастает и имеет предел. Этот предел называют числом е. Следовательно, по определению
В курсе математического анализа доказывается, что эта последовательность монотонно возрастает и имеет предел. Этот предел называют числом е. Следовательно, по определению 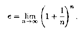 Число е играет большую роль в математике.. Отметим, что число е является иррациональным; его приближенное значение равно е = 2,7182818...
Число е играет большую роль в математике.. Отметим, что число е является иррациональным; его приближенное значение равно е = 2,7182818...
47.Понятие функции
Пусть Х и Y — некоторые числовые множества и пусть каждому элементу x 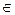 Х по какому-либо закону f поставлен в соответствие один элемент у
Х по какому-либо закону f поставлен в соответствие один элемент у 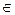 Y. Тогда говорят, что определена функциональная зависимость у от x по закону у = f (x). При этом x называют независимой переменной (или аргументом), у — зависимой переменной, множество Х — областью определения (существования) функции, множество Y — областью значений (изменения) функции. Существуют три основных способа задания функций: табличный, аналитический и графический. 1. Табличный способ широко используется в приложениях. В таких таблицах одну из переменных можно принять за независимое, тогда другие причины будут функциями от этого аргумента. 2. Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде формул. 3. Графический способ. Здесь соответствие между аргументом и функцией задается посредством графика. Область определения функции 1. Когда функция задана в аналитическом виде y = f (x) область ее определения такова: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби = 0, выражение под знаком логарифма должно быть только положительным и др. 2. Область определения функции бывает задана вместе с функцией f(x). Например, 1 ≤ х ≤ 4. Функция у = f(x) называется четной, если для любых значений аргумента из области ее определения выполнено равенство f(-x)=f(x) Функция у = f(x) называется нечетной, если: f(-x)=-f(x)
Y. Тогда говорят, что определена функциональная зависимость у от x по закону у = f (x). При этом x называют независимой переменной (или аргументом), у — зависимой переменной, множество Х — областью определения (существования) функции, множество Y — областью значений (изменения) функции. Существуют три основных способа задания функций: табличный, аналитический и графический. 1. Табличный способ широко используется в приложениях. В таких таблицах одну из переменных можно принять за независимое, тогда другие причины будут функциями от этого аргумента. 2. Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде формул. 3. Графический способ. Здесь соответствие между аргументом и функцией задается посредством графика. Область определения функции 1. Когда функция задана в аналитическом виде y = f (x) область ее определения такова: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби = 0, выражение под знаком логарифма должно быть только положительным и др. 2. Область определения функции бывает задана вместе с функцией f(x). Например, 1 ≤ х ≤ 4. Функция у = f(x) называется четной, если для любых значений аргумента из области ее определения выполнено равенство f(-x)=f(x) Функция у = f(x) называется нечетной, если: f(-x)=-f(x)
48 Предел функции в точке.
Пусть функция f(x) определена на некотором множестве X. Возьмем последовательность точек 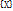 , сходящуюся в точке a. Значения f(x) в этих точках также образуют числовую последовательность: f(
, сходящуюся в точке a. Значения f(x) в этих точках также образуют числовую последовательность: f(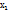 ), f(
), f(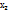 ),…, f(
),…, f(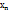 ) (1) Определение1. Число А называется пределом функции f(x) в точке а или пределом функции при х→а, если для любой сходящейся к а последовательности значение аргумента х отличных от а соответствующая последовательность значений функции (1)сходится к числу А. Для обозначения предельного значения функции используется следующая символика:
) (1) Определение1. Число А называется пределом функции f(x) в точке а или пределом функции при х→а, если для любой сходящейся к а последовательности значение аргумента х отличных от а соответствующая последовательность значений функции (1)сходится к числу А. Для обозначения предельного значения функции используется следующая символика: 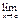 f(x)
f(x) 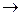 А. Функция f(x) может иметь в точке а только одно предельное значение, поскольку последовательность f(
А. Функция f(x) может иметь в точке а только одно предельное значение, поскольку последовательность f(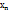 ) имеет только 1 предел.
) имеет только 1 предел.
49 Односторонние пределы
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами
- Число
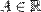 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции 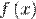 в точке
в точке 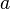 , если для всякой последовательности
, если для всякой последовательности 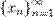 , состоящей из точек, больших числа
, состоящей из точек, больших числа 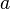 , которая сама сходится к числу
, которая сама сходится к числу 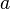 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 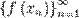 сходится к числу
сходится к числу 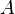 .
.
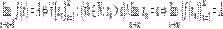
- Число
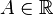 называется левосторонним пределом (левым пределом, пределом слева) функции
называется левосторонним пределом (левым пределом, пределом слева) функции 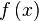 в точке
в точке 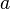 , если для всякой последовательности
, если для всякой последовательности 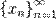 , состоящей из точек, меньших числа
, состоящей из точек, меньших числа 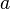 , которая сама сходится к числу
, которая сама сходится к числу 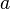 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 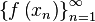 сходится к числу
сходится к числу 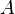 .[1]
.[1]
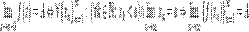
50. Теорема о пределах функций.
Теорема. Пусть функции f(x) и g(x) имеют в точке а пределы, равные соотве






