BIV1. (Аксиома откладывания вектора) Для любой точки AÎEv3 и любого вектора  существует единственная точка BÎ
существует единственная точка BÎ 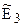 такая, что
такая, что  .
.
BIV2. (Аксиома треугольника) Для любых трех точек A, B, CÎ 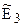 справедливо равенство
справедливо равенство  .
.
Хотя приведенная аксиоматика по своей структуре достаточно проста, построение начал элементарной геометрии на ее основе менее наглядно. Поэтому попытки использования аксиоматики Вейля при построении школьного курса геометрии не получили широкого распространения. Проведем исследование аксиоматики Вейля, докажем ее непротиворечивость, независимость и полноту.
Докажем содержательную непротиворечивость аксиоматики Вейля трехмерного евклидова пространства. Для этого следует с помощью корректных средств построить модель этой системы аксиом. В качестве средств построения искомой модели мы будем использовать аппарат тории чисел.
Теорема 5.2. Аксиоматика Вейля трехмерного евклидова пространства непротиворечива, если непротиворечива арифметика.
Доказательство. Мы докажем содержательную непротиворечивость исследуемой аксиоматики, построив так называемую арифметическуюмодель аксиоматики Вейля. Как было показано в параграфе 2, отсюда следует ее непротиворечивость, при условии непротиворечивости арифметики.
Под вектором будем понимать строку из трех чисел 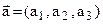 . Таким образом, множество векторов
. Таким образом, множество векторов  представляет собой множество строк, состоящих из трех чисел:
представляет собой множество строк, состоящих из трех чисел: 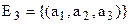 , где
, где  . Точкой также назовем строку из трех чисел
. Точкой также назовем строку из трех чисел  , множество точек
, множество точек 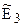 представляет собой множество строк, состоящих из трех чисел:
представляет собой множество строк, состоящих из трех чисел: 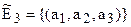 , где
, где  . Операции сложения и умножения вектора на число определим как операции над числовыми строками. Если
. Операции сложения и умножения вектора на число определим как операции над числовыми строками. Если 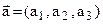 и
и  , то:
, то:
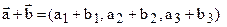 ,
,
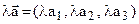 .
.
Под скалярным произведением векторов  и
и  будем понимать число:
будем понимать число:
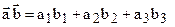 .
.
Пусть даны две точки  и
и  , тогда поставим им в соответствие вектор
, тогда поставим им в соответствие вектор  , равный:
, равный:  .
.
Легко показать, используя групповые свойства действительных чисел относительно операций сложения и умножения, что определенные таким образом точки и векторы, так же, как операции сложения векторов, умножения вектора на число, скалярного произведения и соответствия вектора упорядоченной паре точек, удовлетворяют условиям аксиом BI1 – BIV2 аксиоматики Вейля. Проверим выполнение лишь некоторых аксиом, проверку остальных предоставляем читателю.
Аксиома BI3. В качестве нулевого вектора возьмем строку:  . Если
. Если 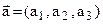 - произвольный вектор, то
- произвольный вектор, то  . Условие аксиомы BI3 выполнено.
. Условие аксиомы BI3 выполнено.
Аксиома BIII2. Пусть даны число l и два вектора  и
и  . Вектор
. Вектор 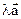 равен:
равен: 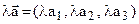 . Поэтому
. Поэтому
 .
.
Условие аксиомы BIII2 выполнено.
Аксиома BIV1. Пусть данаточка  и вектор
и вектор  . Рассмотрим точку
. Рассмотрим точку 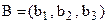 , где
, где  . В силу введенного правила соответствия упорядоченной пары точек и вектора:
. В силу введенного правила соответствия упорядоченной пары точек и вектора:
 .
.
Пусть существует еще одна точка  , такая, что
, такая, что
 .
.
Но тогда,  . Точки В и В¢ совпадают. Условие аксиомы ВIV1 выполнено.
. Точки В и В¢ совпадают. Условие аксиомы ВIV1 выполнено.
Аксиома BIV2. Рассмотрим три точки:  ,
, 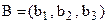 и
и  . Тогда
. Тогда
 Легко видеть, что
Легко видеть, что 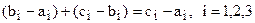 . Отсюда следует:
. Отсюда следует:  . Условие аксиомы ВIV2 выполнено. Теорема доказана.
. Условие аксиомы ВIV2 выполнено. Теорема доказана.
Аксиоматика Вейля трехмерного евклидова пространства обладает свойством минимальности. Любое из утверждений аксиом BI1 – BIV2 не зависит от остальных аксиом.
Теорема 5.2. Аксиоматика Вейля трехмерного евклидова пространства является независимой.
Доказательство. Мы проверим независимость аксиом BIV1 и BIV2 от остальных аксиом исследуемой аксиоматики. Как было указано в параграфе 2, для этого нам следует доказать независимость каждой из этих аксиом от остальных, т.е. доказать непротиворечивость двух аксиоматик, состоящих из всех аксиом Вейля, в которых аксиома BIV1 или аксиома BIV2 заменена ее логическим отрицанием. Так как при этом мы будем использовать аппарат арифметики действительных чисел, то наши рассуждения будут истинными при условии непротиворечивости аксиоматики арифметики действительных чисел.
Прежде всего, рассмотрим аксиому BIV1. Логическое отрицание этой аксиомы имеет вид:
 . Существуют такие точка AÎ
. Существуют такие точка AÎ 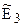 и вектор
и вектор  , что для них можно найти по крайней мере две различные точки В1 и B2, принадлежащие пространству
, что для них можно найти по крайней мере две различные точки В1 и B2, принадлежащие пространству 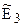 , для которых
, для которых  .
.
Построим арифметическую модель системы аксиом B1 – BIII5,  , BIV2. Понятие вектора, операций сложения векторов, умножения вектора на число и скалярного произведения векторов введем так же, как и при доказательстве теоремы 5.1. Под точкой будем понимать строку из четырех чисел:
, BIV2. Понятие вектора, операций сложения векторов, умножения вектора на число и скалярного произведения векторов введем так же, как и при доказательстве теоремы 5.1. Под точкой будем понимать строку из четырех чисел:  . Пусть даны две точки
. Пусть даны две точки  и
и  , тогда поставим им в соответствие вектор
, тогда поставим им в соответствие вектор  , равный:
, равный:  .
.
Легко видеть, что в построенной модели выполняются все аксиомы BI1 – BIII5 и BIV2, проверьте их самостоятельно. Рассмотрим точку  и вектор
и вектор 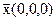 . Тогда для двух различных точек
. Тогда для двух различных точек  и
и  , следуя введенному правилу,
, следуя введенному правилу,  . Условие аксиомы
. Условие аксиомы  для рассматриваемой модели выполнено, ее независимость доказана.
для рассматриваемой модели выполнено, ее независимость доказана.
Сформулируем логическое отрицание аксиомы BIV2:
 . Существуют по крайней мере три точки A, B, CÎ
. Существуют по крайней мере три точки A, B, CÎ 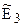 , для которых
, для которых 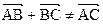 .
.
Для построения арифметической модели системы аксиом B1 – BIII5, BIV1,  понятия вектора и точки, линейных операций над векторами, скалярного произведения и введем так же, как и при доказательстве теоремы 5.1. Упорядоченной же паре точек поставим в соответствие вектор по следующему правилу. Пусть даны две точки
понятия вектора и точки, линейных операций над векторами, скалярного произведения и введем так же, как и при доказательстве теоремы 5.1. Упорядоченной же паре точек поставим в соответствие вектор по следующему правилу. Пусть даны две точки  и
и  , тогда
, тогда  . Рассмотрим три точки
. Рассмотрим три точки  . Вектора
. Вектора  и
и 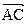 , следуя введенному правилу соответствия, равны:
, следуя введенному правилу соответствия, равны:  . Поэтому
. Поэтому 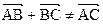 . Независимость аксиомы BIV2 от остальных аксиом Вейля доказана.
. Независимость аксиомы BIV2 от остальных аксиом Вейля доказана.
Мы показали, что аксиоматика Вейля трехмерного евклидова пространства обладает свойствами непротиворечивости и независимости. Покажем, что она также обладает свойством категоричности. Действительно, если мы имеем какую либо модель системы аксиом BI1 – BIV2, то, пользуясь теми же методами, которые использовались в курсах алгебры и аналитической геометрии, можно построить ортонормированный базис пространства  , состоящий из трех векторов, тем самым поставив в соответствие каждому вектору строку из трех чисел, а также систему координат пространства
, состоящий из трех векторов, тем самым поставив в соответствие каждому вектору строку из трех чисел, а также систему координат пространства 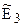 , которая позволяет установить взаимно однозначное соответствие между точкам и строками из трех чисел. При этом линейные операции над векторами, скалярное произведение векторов и соответствие упорядоченной пары точек и векторов в координатах имеют тот же вид, что и в построенной выше арифметической модели этой аксиоматики. Поэтому любая модель аксиоматики Вейля изоморфна ее арифметической модели. Отсюда следует, что любые две модели аксиоматики Вейля трехмерного евклидова пространства изоморфны, а сама аксиоматика категорична. Как отмечалось в параграфе 2, из категоричности аксиоматики следует ее полнота. Таким образом, система аксиом BI1 – BIV2 удовлетворяет условию полноты.
, которая позволяет установить взаимно однозначное соответствие между точкам и строками из трех чисел. При этом линейные операции над векторами, скалярное произведение векторов и соответствие упорядоченной пары точек и векторов в координатах имеют тот же вид, что и в построенной выше арифметической модели этой аксиоматики. Поэтому любая модель аксиоматики Вейля изоморфна ее арифметической модели. Отсюда следует, что любые две модели аксиоматики Вейля трехмерного евклидова пространства изоморфны, а сама аксиоматика категорична. Как отмечалось в параграфе 2, из категоричности аксиоматики следует ее полнота. Таким образом, система аксиом BI1 – BIV2 удовлетворяет условию полноты.






