BIII1. Для любых чисел l, mÎ R, и любых векторов  справедливо равенство
справедливо равенство 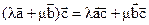 .
.
BIII2. Для любых векторов  справедливо равенство
справедливо равенство  .
.
BIII3. Для любого ненулевого вектора 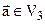 имеет место
имеет место  .
.
Из аксиом ВIII1 – ВIII3 следует, что скалярное произведение представляет собой положительно определенную симметрическую билинейную форму на V3. Будем также предполагать, что:
BIII4. На пространстве V3 задано множество  положительно определенных симметрических билинейных форм, которое включает в себя скалярное произведение векторов, такое, что если
положительно определенных симметрических билинейных форм, которое включает в себя скалярное произведение векторов, такое, что если 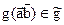 , то
, то  , где l положительное действительной число.
, где l положительное действительной число.
Другими словами, на V3 задано множество  положительно определенных симметрических билинейных форм, пропорциональных скалярному произведению векторов с точностью до положительного числового сомножителя.
положительно определенных симметрических билинейных форм, пропорциональных скалярному произведению векторов с точностью до положительного числового сомножителя.






