Индуктивная связь М в цепи переменного тока возникает вследствие пересечения или объединения магнитных потоков близко расположенных индуктивных элементов (рис.3.21).
Рисунок 3.21 — Различные варианты индуктивной связи двух катушек с током
Индуктивно связанные элементы. Если две катушки с током (контуры тока) расположены вблизи друг друга, то часть магнитного потока одной катушки пронизывает витки второй катушки и наоборот (рис.3.19). При этом изменение тока в одной из катушек приводит к появлению ЭДС во второй катушке. Эта ЭДС называется ЭДС взаимной индукции, а элементы, в которых она возникает — индуктивно связанными элементами.
Собственно индуктивный элемент характеризуется следующими параметрами: индуктивностью 
, количеством витков проводника 
и потоком магнитного поля 
. Величина 
называется потокосцеплением данного индуктивного элемента. Индуктивно связанный элемент помимо собственной индуктивности приобретает дополнительную, «взаимную» индуктивность 
. В зависимости от направленности стороннего магнитного потока относительно собственного магнитного потока данного индуктивного элемента, величина его индуктивности может увеличиваться до величины 
или уменьшаться до 
.
Направление магнитного потока в индуктивном элементе определяется по правилу правого винта и зависит как от направления намотки катушки, так и от направления тока в ней. В индуктивно связанных цепях для определенности принимается, что катушки индуктивности имеют одинаковое направление намотки, тогда взаимодействие их магнитных потоков определяется лишь направлением токов в каждой из катушек, при этом «входные» зажимы или полюсы катушек обозначают на схемах звездочками или точками (рис.3.22).
Ток 
в первой индуктивно связанной катушке (рис.3.22) создает в ней магнитный поток самоиндукции 
. Но, кроме собственного магнитного потока, сквозь витки первой катушки проходит и дополнительный поток взаимной индукции 
, вызванный током 
, протекающим во второй индуктивно связанной катушке. Аналогично, вторую индуктивно связанную катушку наряду с собственным потоком 
пронизывает дополнительный поток 
, вызванный током первой катушки.
Рисунок 3.22 — Согласное и встречное включение катушек индуктивности
Если направления токов в обеих катушках совпадают, то и магнитные потоки катушек сонаправлены; такое включение катушек называют согласным. Тогда полный магнитный поток первой катушки 
, а второй катушки 
, т.е. полный магнитный поток в согласно включенных катушках увеличивается.
Если же направления токов в катушках противоположны, то магнитные потоки катушек также направлены противоположно; такое включение катушек называют встречным. В этом случае полный магнитный поток первой катушки равен 
, а второй катушки 
, т.е. полный магнитный поток во встречно включенных катушках уменьшается.
ЭДС взаимной индукции. Рассмотрим цепь с двумя индуктивно связанными катушками 
и 
, не имеющими электрического контакта (рис.3.23). Катушка подключена к источнику переменного напряжения 
. При изменении тока 
в ней возникает напряжение 
между разомкнутыми зажимами a и b второй катушки . Это напряжение обусловлено возникновением ЭДС взаимной индукции во второй катушке.
Рисунок 3.23 — Цепь с индуктивно связанными катушками,
не имеющими электрического контакта
В рассматриваемой цепи потокосцепление второго контура определяется как 
. В линейной цепи величина потокосцепления пропорциональна величине тока, его порождающего, поэтому 
. Тогда абсолютное значение ЭДС самоиндукции 
, равное величине напряжения 
, наведенного в катушке , составит
.
Воздушный трансформатор. Устройство, построенное по схеме рис.3.23, в технике имеет название «воздушный трансформатор». Трансформатор позволяет осуществить преобразование уровня сигнала при передаче от одного контура цепи к другому с помощью исключительно индуктивной связи. Отсутствие электрической связи между обмотками трансформатора позволяет осуществить «гальваническую развязку» контуров цепи.
В трансформаторе катушка имеет название первичной обмотки, а катушка — вторичной обмотки. Чтобы обеспечить согласование различных цепей электрического устройства по напряжению, применяют трансформаторы с различным количеством витков в первичной и вторичной обмотках. Если 
, трансформатор называют понижающим (напряжение во вторичной цепи понижается), а при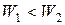 
трансформатор является повышающим. При 
трансформатор не изменяет уровня сигнала, а только выполняет роль гальванической развязки между первичной и вторичной цепями.
Воздушные трансформаторы имеют ограниченное техническое применение, более широко используются трансформаторы со стальным магнитопроводом (сердечником), которые позволяют значительно увеличить индуктивную связь между обмотками трансформатора.
Учет индуктивной связи при расчете цепи. При расчете электрических цепей с индуктивно связанными элементами необходимо учитывать изменение индуктивности за счет появления взаимной индуктивности , что приводит к изменению падения напряжения на индуктивно связанном элементе. Как указывалось выше, напряжение на любом индуктивном элементе зависит от величины тока, проходящего через элемент, а, значит, и от величины собственного магнитного потока. При наличии индуктивной связи в элемент вносится дополнительный магнитный поток, способный увеличить или уменьшить его реактивное сопротивление. Величина этого сопротивления зависит от способа включения индуктивно связанных элементов — встречного или согласного (рис.3.22, 3.24). При согласном включении установятся напряжения:
на первой катушке 
,
на второй катушке 
.
а б
Рисунок 3.24 — Электрическая схема индуктивно связанных катушек
при согласном (а) и встречном (б) включении
При встречном включении установятся напряжения:
на первой катушке 
,
на второй катушке 
.
Закон Ома для неразветвленной цепи с двумя индуктивно связанными элементами. Рассмотрим цепь, состоящую из двух реальных индуктивно связанных катушек, соединенных последовательно. В этом случае возможны два варианта включения катушек — согласное и встречное (рис.3.25).
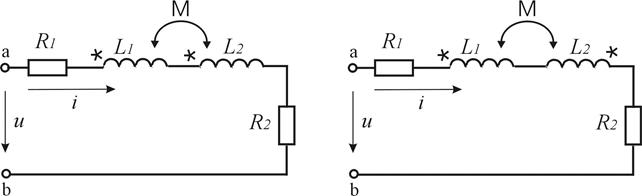
а б
Рисунок 3.25 — Последовательная цепь из двух индуктивно связанных катушек и ее векторные диаграммы при согласном (а) и встречном (б) включении
Поскольку при последовательном соединении через обе катушки протекает один и тот же ток 
, напряжения на них составят:
при согласном включении (рис.3.25а)
, 
;
при встречном включении (рис.3.25б)
, 
.
Запишем уравнение по закону Ома для всей цепи (рис.3.25):
при согласном включении 
,
в комплексной форме 
;
при встречном включении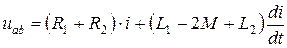 
,
в комплексной форме 
.
Из приведенных соотношений и векторных диаграмм (рис.3.25) видно, что за счет индуктивной связи в последовательной цепи происходит следующее:
— при согласном включении эквивалентная индуктивность цепи возрастает на величину 
, при этом увеличивается реактивная составляющая полного сопротивления, а значит, возрастает и напряжение ;
— при встречном включении эквивалентная индуктивность цепи уменьшается на величину , при этом уменьшается напряжение .
Полученный вывод позволяет на практике определить способ включения индуктивно связанных катушек. Если в одном случае произвольно соединить катушки последовательно и измерить напряжение цепи , а в другом — поменять местами выводы одной из катушек и опять измерить , то в каком-то случае это напряжение окажется больше, что и соответствует согласному включению катушек. Кроме этого, по результатам таких измерений можно вычислить величину сопротивления взаимной индуктивности 
. При согласном включении катушек это сопротивление носит характер «добавочной» индуктивности, а при встречном включении оно оказывает на цепь «емкостной» эффект (см.векторные диаграммы рис.3.25).
В 
-цепи с индуктивно связанными элементами изменение реактивного сопротивления за счет сопротивления взаимной индуктивности влечет за собой изменение резонансных свойств цепи.
Законы Кирхгофа для разветвленной цепи с двумя индуктивно связанными элементами. Уравнения по первому закону Кирхгофа для цепей с индуктивными связями составляются аналогично уравнениям для обычной цепи переменного тока. При составлении уравнений по второму закону Кирхгофа для цепей с индуктивно связанными элементами задают направления токов и определяют, как включены катушки (встречно, согласно). Задают направления обхода контуров и составляют уравнения с учетом взаимоиндуктивных падений напряжений в ветвях с индуктивно связанными катушками.
При составлении уравнений по второму закону Кирхгофа необходимо помнить, что в случае согласного включения катушек знак взаимоиндуктивного падения напряжения такой же, как и знак собственного падения напряжения на индуктивности катушки. При встречном же включении знаки взаимоиндуктивного и собственного падения напряжения на индуктивности противоположны.
Составим уравнения по второму закону Кирхгофа для двухконтурной цепи, представленной на рис.3.26.
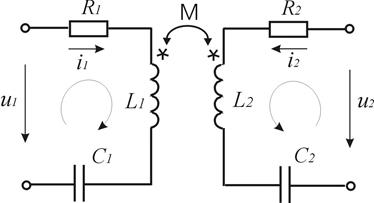
Рисунок 3.26 — Двухконтурная цепь с индуктивной связью
В рассматриваемой цепи катушки включены согласно, поэтому взаимоиндуктивные падения напряжений в каждой из них записываются в уравнениях с тем же знаком, что и падения напряжения за счет собственной индуктивности: 
;
.
В комплексной форме эти уравнения примут вид:
;
.
На составлении уравнений по законам Кирхгофа основаны метод законов Кирхгофа и метод контурных токов, которые применимы для расчетов сложных цепей с индуктивными связями. Остальные известные методы расчетов практически неприменимы из-за сложности учета ЭДС взаимоиндукции.
Определим токи в ветвях цепи с параллельным соединением двух индуктивно связанных катушек (рис.3.27), используя МЗК и МКТ. В случае параллельного соединения общей величиной для обеих ветвей с катушками является входное напряжение 
. В цепи — два узла и три ветви, два независимых контура, направления обхода которых для обоих методов зададим одинаково (рис.3.27).
Система уравнений по МЗК для цепи (рис.3.27а) имеет вид:
.
Рисунок 3.27 — Параллельная цепь из двух индуктивно связанных катушек, включенных согласно (а) и встречно (б)
Составим систему из двух уравнений по МКТ. При определении комплексов собственных сопротивлений контуров учитываются только индуктивные связи между катушками, входящими в данный контур. Тогда в связанных одним и тем же контурным током катушках индуцируются одинаковые ЭДС взаимной индукции. Поэтому в выражении для собственного сопротивления появятся одинаковые слагаемые вида 
. Если относительно данного контурного тока катушки включены согласно, то знак слагаемого 
— положительный, а при встречном включении — отрицательный.
При определении комплекса взаимного сопротивления знак слагаемого вида определяется так: если направления контурных токов в катушке 
и катушке 
таковы, что относительно этих токов катушки включены согласно, то знак слагаемого положительный, если относительно этих токов катушки включены встречно — знак отрицательный.
Применим МКТ для нахождения токов в цепи с согласно включенными катушками (рис.3.27а). Зададимся направлениями контурных токов. Составим систему уравнений в комплексной форме:
.
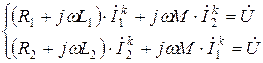Обозначим собственные сопротивления контуров: 
, 
, а общее сопротивление: 
. В данной схеме ток в неразветвленной части схемы составит 
, где 
, 
. Тогда система уравнений примет вид:
.
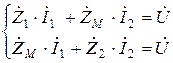Запишем решение системы уравнений: 
; 
; а общий ток составит 
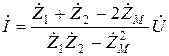. Отсюда получим выражение для входного комплексного сопротивления цепи: 
. При отсутствии индуктивной связи (
) получим известное выражение для сопротивления параллельного соединения. Эквивалентные сопротивления ветвей при согласном включении: 
; 
.
При нахождении токов в цепи со встречно включенными катушками (рис.3.27б) аналогично получим: 
; 
;
, откуда входное сопротивление 
.
Эквивалентные сопротивления ветвей при встречном включении: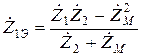 
; 
.
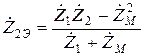Запишем системы уравнений по МЗК и МКТ для цепи, приведенной на рис.3.28. В этой цепи три катушки попарно охвачены индуктивной связью.
Рисунок 3.28 — Разветвленная цепь с тремя индуктивными связями
Отметим, что при выбранных направлениях токов в ветвях катушка включена согласно с 
, а с и с — встречно.
Система уравнений по МЗК:
,
Система уравнений по МКТ:
Здесь в выражении для взаимного сопротивления 
все слагаемые, учитывающие взаимную индуктивность, отрицательные, поскольку все катушки относительно соответствующих контурных токов включены встречно.
