Представление синусоидальной функции времени вращающимся вектором. При анализе и расчете сложных цепей переменного тока возникает необходимость совместного рассмотрения нескольких синусоидальных сигналов одинаковой частоты, между которыми есть фазовый сдвиг. Можно представить эти сигналы в привычном графическом виде (рис.3.3), однако в таком виде выполнение математических действий над ними оказывается достаточно трудоемким. Более простым и наглядным является представление синусоидальных функций с помощью вращающихся векторов (рис.3.7, 3.8).
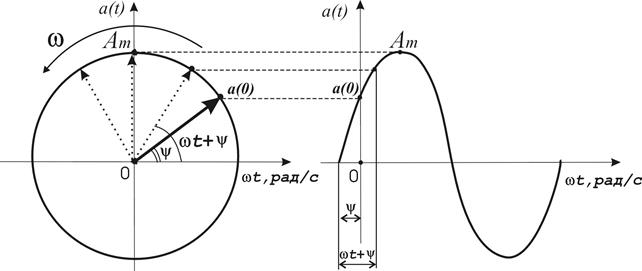
Рисунок 3.7 — Представление синусоидальной функции
вращающимся вектором
Синусоидальная функция 
может быть представлена вектором, длина которого равна амплитуде функции 
. В начальный момент времени 
вектор расположен под углом 
к горизонтальной оси. При увеличении 
вектор равномерно вращается против часовой стрелки с угловой скоростью 
.
Длина проекции вращающегося вектора на ось 
в любой момент времени будет равна соответствующему мгновенному значению функции .
Таким образом, любой синусоидальный сигнал можно представить в виде вектора, равномерно вращающегося с угловой скоростью, равной угловой частоте сигнала. Начальное положение вектора определяется начальной фазой сигнала, длина вектора — амплитудным значением сигнала. При таком представлении синусоидальных сигналов выполнение любых математических действий над ними сводится к операциям над соответствующими векторами (рис.3.8). Изображение на координатной плоскости совокупности таких векторов с учетом их взаимной ориентации по фазе называется векторной диаграммой (рис.3.8 б).
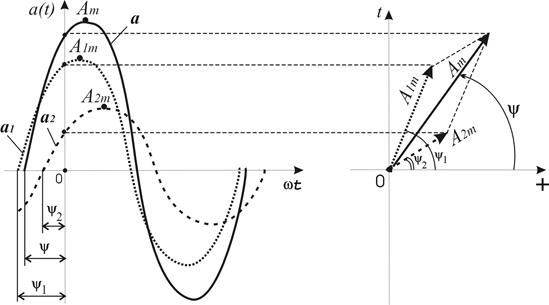
а б
Рисунок 3.5 — Сложение двух синусоидальных функций:
а — графическое сложение; б — сложение с помощью векторной диаграммы
Представление синусоидальной функции комплексным числом. Вращающийся вектор, изображающий синусоидальную функцию, можно описать комплексным числом. Для этого нужно расположить вектор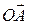 
в комплексной плоскости (рис.3.6).
Рисунок 3.6 — Перенос вектора на комплексную плоскость
Представление вращающегося вектора комплексным числом дает возможность заменить геометрические действия над векторами алгебраическими действиями над соответствующими комплексными числами.
Пусть в начальный момент 
вектор 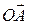(радиус-вектор) неподвижен (рис.3.6), тогда его можно представить комплексным числом
,
где 
— модуль комплексного числа 
(всегда положителен);
— аргумент комплексного числа (имеет любой знак);
— мнимая единица или оператор поворота на 900, 
.
Для любого момента 
вращающемуся вектору 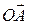соответствует комплексное число
,
где 
— оператор поворота вектора с круговой частотой ω.
В электротехнике при описании гармонического сигнала 
величину называют комплексной амплитудой, а величину 
— комплексной гармонической функцией. Величина 
называется комплексным действующим значением.
Формы записи комплексных величин. В зависимости от поставленной задачи анализа и расчета цепей синусоидального тока применяются различные формы записи комплексных величин.
Амплитуда (модуль) и фаза (аргумент) определяют показательную форму записи комплексного числа : ,
а также тригонометрическуюформу записи: 
.
Проекции вектора 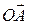на «действительную» и «мнимую» оси комплексной плоскости (величины 
и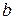 
) определяют алгебраическую форму записи комплексного числа : 
.
При выполнении действий с комплексными числами зачастую приходится менять форму их записи. Для этого существуют формулы перехода
; 
; 
; 
; 
.
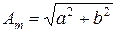Сложение и вычитание комплексных чисел удобно производить в алгебраической форме, а умножение, деление и возведение в степень — в показательной.
Число 
называется комплексно-сопряженным числу 
. Произведение комплексно-сопряженных чисел — вещественное число, равное квадрату их модуля: 
.
