Гипербола

Определение. Гипербола – геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная большой оси гиперболы.

Эта разность по модулю должна быть меньше расстояния между фокусами и отлична от нуля.

и - фокусные радиусы точки .

(по определению) следовательно .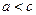

Гипербола состоит из двух отдельных частей, называемых ветвями.

Канонический вид уравнения

, (11)

следовательно,

.

Уравнение – это уравнение прямой с угловым коэффициентом . При .

Прямые называются асимптотами гиперболы.

Отрезки и - оси гиперболы.

Уравнение вида задает гиперболу, сопряженную с первой.

Гипербола с равными полуосями называется равносторонней:

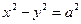
Определение. Эксцентриситетом гиперболы называется отношение расстояния между фокусами к расстоянию между вершинами:

. (12)

Определение. Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, расположенные симметрично относительно центра на расстоянии 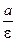от него, называются директрисами гиперболы.

Теорема. Для любой точки эллипса и гиперболы справедливо соотношение

, (13)

где – расстояние от точки до фокуса , а 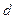– расстояние до соответствующей директрисы.