Дано: эллипс с фокусами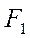 
и 
, 
– большая полуось, 
– половина расстояния между фокусами.
Возьмем за ось абсцисс прямую 
, а точку 
поместим на середине отрезка 
. Пусть 
– произвольная точка плоскости. Пусть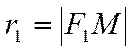 
, 
.
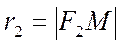По определению эллипса точка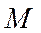 
принадлежит эллипсу тогда и только тогда, когда
. (7)
Координаты фокусов равны соответственно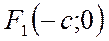 
, 
, следовательно
, 
.
Подставим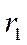 
и 
в (7):
+ 
= 
. (8)
(8) – уравнение эллипса в заданной системе координат. Преобразуем его к виду 
= 
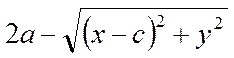и возведем в квадрат обе части уравнения:
;
; возведем в квадрат еще раз:
;
.
Обозначим 
, получим 
.
После приведения к каноническому виду уравнение эллипса запишется так:
. (9)
Эллипс, определяемый уравнением 
, симметричен относительно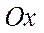 
и 
. 
- центр эллипса, 
и 
- большая и малая полуоси эллипса.
При 
получаем 
- уравнение окружности.
Определение. Эксцентриситет эллипса – отношение расстояния между фокусами к длине его большей оси: 
. (10)
Так как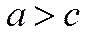 
, следовательно 
< 1.
, следовательно, 
.
Определение. Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 
от него, называется директрисами эллипса.
Их уравнения: 
и 
. Так как 
, следовательно, 
.
