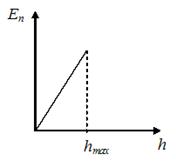
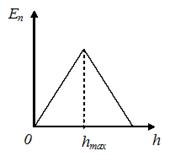
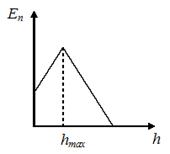
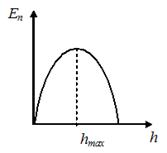
1. График зависимости потенциальной энергии тела, брошенного с поверхности земли под некоторым углом к горизонту, от высоты подъема имеет вид, показанный на рисунке …
Решение:
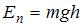
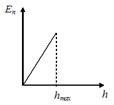
Зависимость 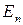 линейно зависит от
линейно зависит от 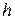 и после достижения
и после достижения 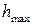 уменьшается вместе с
уменьшается вместе с 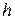 .
.
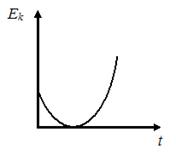
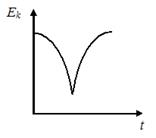
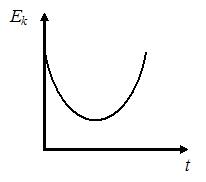
2. График зависимости кинетической энергии от времени для тела, брошенного с поверхности земли под некоторым углом к горизонту, имеет вид, показанный на рисунке …
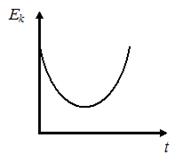
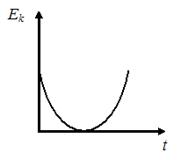
 Решение:
Решение:
1. 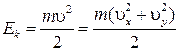 , где
, где 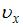 и
и 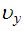 – проекции скорости тела на оси OX и OY соответственно.Здесь
– проекции скорости тела на оси OX и OY соответственно.Здесь 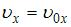 ,
, 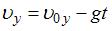 . Тогда
. Тогда 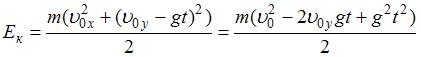 .
.
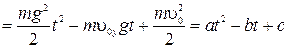 ,
, 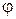 - угол броска. Это ур-е параболы со смещенной вершиной, ветви которой направлены вверх.
- угол броска. Это ур-е параболы со смещенной вершиной, ветви которой направлены вверх.
(Т.к. равномерное дв. по гориз. есть всегда, то 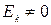 ).
).
Решение:
Т.к. нет неконсерв. сил. Следовательно,.
2. 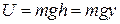 ,
, 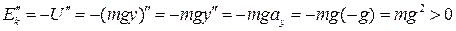 , т.е рис.1
, т.е рис.1
(,).
3. Теннисный мяч летел с импульсом 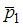 в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью
в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 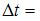 0,1 с. Изменившийся импульс мяча стал равным
0,1 с. Изменившийся импульс мяча стал равным 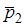 (масштаб указан на рисунке). Средняя сила удара равна …
(масштаб указан на рисунке). Средняя сила удара равна …
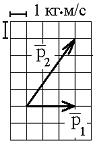
Решение:
Изменение импульса мяча равно 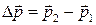 . Из теоремы Пифагора следует. что
. Из теоремы Пифагора следует. что 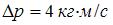 (см. рис.). Так как
(см. рис.). Так как 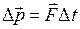 , то
, то 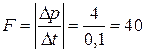 Н
Н
 4. На теннисный мяч, который летел с импульсом
4. На теннисный мяч, который летел с импульсом 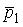 , на короткое время
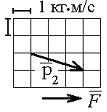
, на короткое время 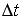 = 0,01 с подействовал порыв ветра с постоянной силой F = 300 Н, и импульс мяча стал равным
= 0,01 с подействовал порыв ветра с постоянной силой F = 300 Н, и импульс мяча стал равным 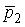 (масштаб и направление указаны на рисунке). Величина импульса
(масштаб и направление указаны на рисунке). Величина импульса 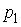 была равна …
была равна …
33,2 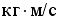 ; 6,2
; 6,2 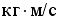 ; 6,1
; 6,1 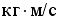 ; 1
; 1 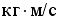 ; 5
; 5 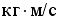
Решение:
Т.к. 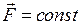 , то
, то 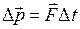 ,
, 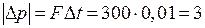 кг∙ м/с и
кг∙ м/с и 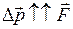
Изменение импульса мяча равно 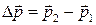 , т.е.
, т.е. 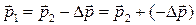 . Строим.
. Строим.
Из построения следует, что 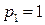
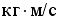
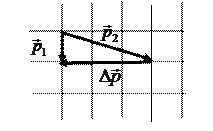
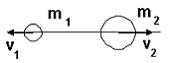
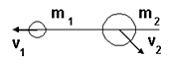
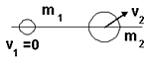
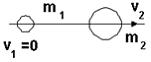
 5. Шар массы
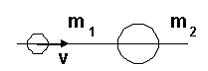
5. Шар массы 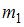 , имеющий скорость v, налетает на неподвижный шар массы
, имеющий скорость v, налетает на неподвижный шар массы 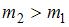 .После соударения шары будут двигаться так, как показано на рисунке …(Видимо v2
.После соударения шары будут двигаться так, как показано на рисунке …(Видимо v2 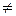 v)
v)
| |
| |
| |
|
Решение:
Т.к. 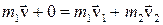 , т.е.
, т.е. 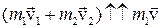 - 2 и 3 рис. не верны.
- 2 и 3 рис. не верны.
Налетающее тело после упруг. удара о покоящееся остановиться, только если 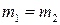 (4 неверно)
(4 неверно)
 прав. рис.1
прав. рис.1
 6. Сплошной цилиндр и шар, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми скоростями на горку. Если трением и сопротивлением воздуха можно пренебречь, то отношение высот
6. Сплошной цилиндр и шар, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми скоростями на горку. Если трением и сопротивлением воздуха можно пренебречь, то отношение высот 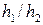 , на которые смогут подняться эти тела, равно (трением о горку пренебречь нельзя)
, на которые смогут подняться эти тела, равно (трением о горку пренебречь нельзя)
Решение:
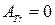 ,
, 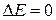
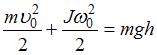 , где J – момент инерции тела относительно оси, проходящей через центр масс,
, где J – момент инерции тела относительно оси, проходящей через центр масс, 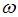 – угловая скорость вращения вокруг этой оси,
– угловая скорость вращения вокруг этой оси, 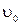 - скорость центра инерции, h – высота, на которую сможет подняться тело (Отсчитываем потен. энергию от основания горки).
- скорость центра инерции, h – высота, на которую сможет подняться тело (Отсчитываем потен. энергию от основания горки).
Нет проскальзывания, 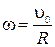 , получаем:
, получаем: 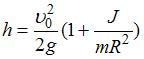 .
.
Сплошной цилиндр - 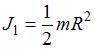 (
(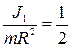 ), шар -
), шар - 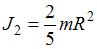 (
(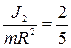 ).
).
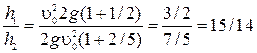
7. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки с одной и той же высоты. Если трением и сопротивлением воздуха можно пренебречь, то отношение скоростей 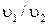 , которые будут иметь эти тела у основания горки, равно … (трением о горку пренебречь нельзя)
, которые будут иметь эти тела у основания горки, равно … (трением о горку пренебречь нельзя)
Решение:
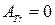 ,
, 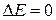
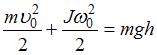 , где J – момент инерции,
, где J – момент инерции, 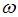 – угловая скорость,
– угловая скорость, 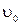 - скорость центра инерции, h – высота. (Отсч.потен. энергию от осн. горки).
- скорость центра инерции, h – высота. (Отсч.потен. энергию от осн. горки).
Нет проскальзывания, 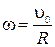 , получаем
, получаем 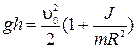 или
или 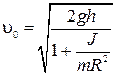
Для сплошн. цилиндра - 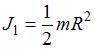 (
(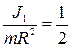 ), для полого цилиндра -
), для полого цилиндра - 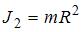 (
(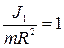 ).
).
Тогда искомое отношение скоростей 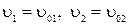 равно
равно 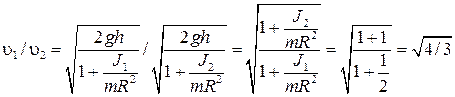 .
.
8. Горизонтально летящая пуля пробивает брусок, лежащий на гладкой горизонтальной поверхности. В системе «пуля – брусок» …

| имп. сохр., мех. энергия не сохр. | ||
| имп. сохр, мех. энергия сохр. | |||
| имп. не сохр, мех. энергия сохр. | |||
| имп. не сохр, мех. энергия не сохр. |
Решение:
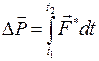 ,
, 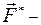 равнод. внешних сил
равнод. внешних сил
По гориз. (по напр. движения) на систему тел не действуют никакие внеш. силы (трения о гладкий стол нет). Следовательно, 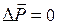 - импульс сохраняется.
- импульс сохраняется.
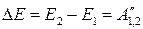 ,
,  -работа неконсерв. сил
-работа неконсерв. сил
Имеется необр. деформации бруска (неконсерв. сила) и ее работа не равна 0, т.е. 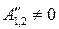 - мех. энергия не сохр. (уменьшается).
- мех. энергия не сохр. (уменьшается).
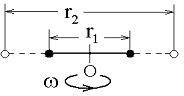 9. Два шарика закреплены на невесомом длинном стержне на расстоянии
9. Два шарика закреплены на невесомом длинном стержне на расстоянии 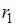 друг от друга. Стержень вращ. без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками, с угловой скоростью
друг от друга. Стержень вращ. без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками, с угловой скоростью  . Если шарики раздвинуть симметрично на расстояние
. Если шарики раздвинуть симметрично на расстояние 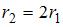 , то угловая скорость
, то угловая скорость 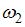 будет равна …
будет равна …
Решение:
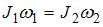 . Здесь J – момент инерции шариков относительно оси вращения,
. Здесь J – момент инерции шариков относительно оси вращения, 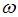 – угловая скорость вращения вокруг этой оси.
– угловая скорость вращения вокруг этой оси.
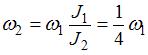 . Таким образом, угловая скорость уменьшится в 4 раза.
. Таким образом, угловая скорость уменьшится в 4 раза.
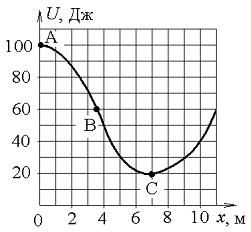 10. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике
10. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 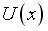 . Кинетическая энергия шайбы в т. С … и т.В
. Кинетическая энергия шайбы в т. С … и т.В
Решение:
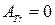 ,
, 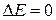 , т.е.
, т.е. 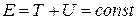
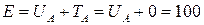 Дж.
Дж.
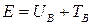 ,
, 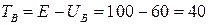 Дж,
Дж,
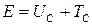 ,
, 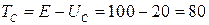 Дж
Дж
Следовательно, 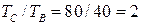 .
.
Кинет. энергия шайбы в т. С в 2 раза больше, чем в т. В.
11. С ледяной горки с небольшим шероховатым участком АС из точки А без начальной скорости скатывается тело. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 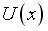 . При движении тела сила трения совершила работу
. При движении тела сила трения совершила работу 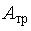 = 20 Дж .(Ошибка, должен быть минус) После абсолютно неупругого удара тела со стеной в точке В выделилось тепла
= 20 Дж .(Ошибка, должен быть минус) После абсолютно неупругого удара тела со стеной в точке В выделилось тепла
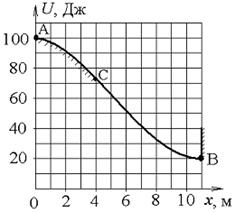
Решение:
При удара о стенку в т.В потенциальная энергия тела не изменилась (до удара и после 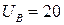 Дж), а кинетическая в т.В вся перешла в тепло, т.к. тело остановилось (до удара
Дж), а кинетическая в т.В вся перешла в тепло, т.к. тело остановилось (до удара 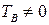 после
после 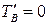 Дж)т.е.
Дж)т.е.
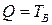
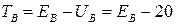 Дж
Дж
На участке от С до В полная энергия сохраняется 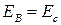
На участке от А до В: 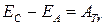 , т.е.
, т.е. 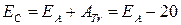 Дж
Дж
В т.А: 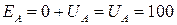 Дж. Тогда
Дж. Тогда
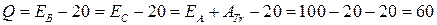 Дж.
Дж.






