Хід роботи. 1. F-критерій Фішера (F-розподіл).Для перевірки Н0-гипотези про рівність дисперсій ( ) генеральних сукупностей, що розподіляються нормально t-критерій

1. F-критерій Фішера (F-розподіл). Для перевірки Н₀-гипотези про рівність дисперсій () генеральних сукупностей, що розподіляються нормально t-критерій виявляється недостатньо точним, особливо при оцінці різниці дисперсій невеликих вибірок. У пошуках кращого критерію Р. Фішер винайшов, що замість вибіркової різниці s₁–s₂ зручніше використовувати різницю між натуральними логарифмами цих величин, тобто ln s₁ – ln s₂, де s₁≥s₂. Ця різниця, позначена Фішером буквою z, розподіляється нормально за наявності як великих, так і середніх за об'ємом статистичних сукупностей. При визначенні величини z можна замість ln використовувати lg. Д. Снедекор запропонував замість логарифма використовувати показники вибіркових дисперсій, позначивши цей показник буквою F

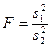при (42)

Оскільки прийнято брати відношення більшої дисперсії до меншої, то F≥1. Якщо , то F=1. Чим значніше нерівність між вибірковими дисперсіями, тим більше буде і величина F і навпаки. Величина F має безперервну функцію розподілу і залежить тільки від числа ступенів свободи. F повністю визначається вибірковими дисперсіями і не залежить від генеральних параметрів, оскільки припускають, що порівнювані вибірки, які характеризуються дисперсіями і , взяті з генеральних сукупностей з або з однієї і тієї ж генеральної сукупності.

Критичні точки для F-критерію містяться в таблиці, яка додається до практичного заняття. У цій таблиці ступені свободи для більшої дисперсії k₁ розташовані у верхньому рядку (по горизонталі), а ступені свободи для меншої дисперсії k₂ – в першій графі (по вертикалі). Якщо вибірки, що порівнюються беруть з однієї і тієї ж генеральної сукупності або з різних сукупностей з дисперсіями і , рівними одна одній: , то величина F-критерію не перевищить критичної точки (F_st) (додаток 5). Якщо ж вибірки взяті з різних сукупностей з їх параметрами і , не рівними один одному, то F_ф≥F_st і нульова гіпотеза має бути знехтувана.

 

Таблиця 26 – Вплив Pb на асиміляційну поверхню білої акації

Площа асиміляційної поверхні, см2	Відхилення від середньої арифметичної	Квадрати відхилень
дослід	контроль	дослід	контроль	дослід	контроль
∑=5104 =638	∑=4734 =526	- -	- -	∑=18174	∑=28632
∑=46806

Приклад 1. У табл. 26 містяться дані про вплив свинцю на площу асиміляційної поверхні 4-х місячних саджанців білої акації (Robinia pseudoacacia L.). Контрольні рослини зростали в умовно чистій зоні.

Розраховані для цих даних дисперсії такі: у дослідній групі , в контролі .

У таблиці, яка додається до лабораторного заняття для 5%-ного рівня значущості (Р=0,05) і числа ступенів свободи k₁=9–1=8 (верхній рядок таблиці) і k₂=8–1=7 (перша графа тієї ж таблиці) знаходимо F_st=3,5. Оскільки F_ф<F_st, нульова гіпотеза залишається в силі (Р>0,05). Це означає, що генеральні параметри груп, що порівнюються і що застосування t-критерію для перевірки Н₀-гипотези відносно оцінки різниці між вибірковими середніми і має достатні підстави.

2. Оцінка різниці між коефіцієнтами варіації. Коефіцієнт варіації обчислюється за формулою

(43)

е Сυ – коефіцієнт варіації; s – середнє квадратичне відхилення; – середнє значення ознаки.

Різниця між коефіцієнтом варіації груп, що порівнюються які беруть із сукупностей з нормальним розподілом, можна оцінити за допомогою t-критерію Ст’юдента. Наближеною оцінкою різниці Сυ₁–Сυ₂=d_Cυ є її відношення до своєї помилки, яка дорівнює кореню квадратному з суми помилок коефіцієнтів варіації порівнюваних груп.

(44)

(45)

Нульову гіпотезу відкидають, якщо t_ф>t_st для прийнятого рівня значущості й числа ступенів свободи k=n₁+n₂–2.

Приклад 2. З табл. 26 видно, що дослідні (n₁=8) і контрольні (n₂=9) 4-х місячні саджанці білої акації характеризуються середніми и см². и . Звідси і . Різниця d_Cυ=11,4–8,0=3,4 %. Розрахуємо помилки цих показників за формулою (45):

Ця величина не перевершує критичну точку t_st=2,13 для k=8+9–2=15 і α =5 %, що не дає підстави для відкидання нульової гіпотези.

Різницю між коефіцієнтами варіації можна оцінити шляхом зіставлення довірчих інтервалів, розрахованих для генеральних параметрів груп, що порівнюються. При цьому межі довірчих інтервалів визначають за формулами:

(46) (47)

де Р_н – нижня, а Р_в – верхня межі довірчого інтервалу; ; t – нормоване відхилення (для α=5 % t=1,96).

Визначимо межі довірчого інтервалу для дослідної групи, відобразив коефіцієнт варіації в долях одиниці, тобто Сυ =0,08:

; або 5,3 %;

або 16,7 %.

Аналогічно визначаємо межі довірчого інтервалу для контрольної групи:

; або 7,6 %;

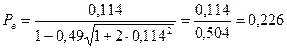або 22,6 %.

Отже, в першому випадку межі довірчого інтервалу опинилися від 5,3 до 16,7 %, у другому – від 7,6 до 22,6 %. Таким чином, межі довірчого інтервалу, побудованого для контрольної групи, близькі до меж інтервалу дослідної групи саджанців акації білої, що вказує на відсутність істотних відмінностей між коефіцієнтами варіації цих груп.