Хід роботи

Ще Гіппократ в VI сторіччя до н.е. звернув увагу на наявність зв'язку між статурою і темпераментом людей, між будовою тіла і схильністю до тих або інших захворювань. Певні види подібного зв'язку виявлені також і в тваринному й рослинному світі. Наприклад, відомий зв'язок між якістю насіння і врожайністю культурних рослин. У рослин і тварин закономірності зв'язків ускладнюються тим, що зазвичай кожному певному значенню однієї з ознак відповідає не одне значення іншої ознаки, а ціла сукупність значень. Такі часткові зв'язки між ознаками, чинниками, подіями, характеристиками називаються кореляційними.

1. Побудова кореляційної сітки і кореляційної таблиці. При безпосередньому аналізі отриманих даних важко скласти якесь уявлення про наявність зв'язаності між ознаками. Більш ясна картина виходить у тому випадку, якщо дані табл. 27 відобразити графічно, у вигляді точкової діаграми (рис. 8). Місцеположення спостереження визначається перетином осей абсциси й ординати. Така систематизація первинних спостережень вже дає відоме уявлення про наявність корелятивного зв'язку. Іншим способом зображення кореляції є складання кореляційної таблиці (або решітки) (табл. 27).

 

 

Таблиця 27 – Довжина колоса (Х) і число зерен (Y) у рослин ячменю

№ рослини	Х	Y	№ рослини	Х	Y	№ рослини	Х	Y

 

									·	·
Довжина колосу (см)										··
							·	·	·
						·	···	····	··
			·		···	····	···	·
			·		····	···	·	·
		·	··	··	·	·
		·	··		·

14 16 18 20 22 24 26 28 30 32 34

Число зерен

 

Рис. 8 – Розподіл 50 рослин ячменю за довжиною колоса і числом зерен

 

У неї послідовно переносять результати первинних спостережень. Місце кожного спостереження визначається одночасно за рядком Х і графою Y. Після перенесення всіх даних (для перевірки проводиться двічі) підраховують число точок у кожній клітці і в ній же записують результати. Ці числа означають кількість варіант, що мають однакове значення ознак Х і Y. Так, число 2 на перетині строки 8 і графи 19 показує, що в даній вибірці були 2 рослини, що мали довжину колоса 8 см і 19 зерен у колосі (табл. 28).

 

Таблиця 28 – Кореляційна таблиця

Довжина колосу в см (Х)	Число зерен у колосі (Y)	Сума за строками fx	ax	fax	fax2
	· 1 (6)	·· 2 (3)	· 1 (0)					–3	–12		19,0
	· 1 (4)	·· 2 (2)	··· 3 (0)	· 1 (–2)				–2	–14		20,7
		· 1 (1)	··· 3 (0)	···· 4 (–1)	·· 2 (–2)			–1	–10		24,1
			··· 3 (0)	····· 5 (0)	··· 3 (0)	· 1 (0)					25,5
				·· 2 (1)	······ 6 (2)	·· 2 (3)					28,0
					·· 2 (4)	· 1 (6)					29,0
					· 1 (6)	· 1 (9)					29,5
						·· 2 (12)					31,0
Сума за графами fy								–	–6
ay	–2	–1		+1	+2	+3	–
fay	–4	–5
fay2

 

Потім підраховують частоти кожного рядка, що дає f_x і кожної графи, що дає f_y. Суми всіх частот, що обчислені окремо за підсумковим рядком і підсумковою графою, повинні дорівнювати один одному, вони представляють загальне число спостережень (n). При аналізі цієї таблиці видно, що є пряма кореляція: у довших колосів у середньому більше зерен. Кожен горизонтальний і вертикальний ряди є вибіркою з нормальним розподілом ознак, що варіюють.

Більш рельєфною виявляється залежність кількості зерен у колосі від його довжини, якщо зіставити зміну довжини колоса з числом зерен у колосі. Ці дані наведені в стовпці . У кожному рядку перемножують число випадків в окремій клітці на відповідне їй значення ряду Y, сума ділиться на f_x кожного рядка. Наприклад, для першого рядка: (16·1+19·2+22·1):4=19,0; для другого – (16·1+19·2+22·3+25·1):7=20,7 і так далі. З табл. 28 видно, що в міру збільшення довжини колоса зростає середня кількість зерен.

За прямої лінійної кореляції частоти групуються біля діагоналі, проведеної з лівого верхнього до правого нижнього кута. При зворотній – з верхнього правого до нижнього лівого кута таблиці, а середні значення однієї ознаки убувають у міру збільшення іншої. За відсутності кореляції частоти розташовуються більш менш рівномірно, а середнє значення і не змінюються залежно від варіювання значень Х і Y.

2. Обчислення коефіцієнта кореляції. Коефіцієнт кореляції прямим способом обчислюють за формулою

(48)

Можна користуватися допоміжними формулами:

(49)

(50)

(51)

За відсутності кореляції, тобто якщо ознаки варіюють незалежно одна від одної, будь-яке із значень може поєднуватися як з позитивними, так і з негативними 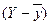однаково часто. Позитивних здобутків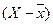 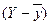буде стільки ж, скільки і негативних, і сума здобутків буде дорівнювати або майже дорівнювати нулю. Якщо ознаки варіюють зв'язано, то відхилення 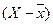поєднуватимуться не з будь-якими, а тільки з деякими відхиленнями 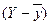. При прямій кореляції позитивні відхилення 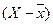будуть переважно поєднуватимуться з позитивними, а негативні 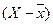– з негативними 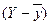. Тобто, здобутки відхилень будуть переважно однозначними, і сума їх – позитивною. При зворотній кореляції поєднуються переважно відхилення з різними знаками, і сума їх здобутків буде негативна. І в тому і в іншому випадку сума здобутків буде тим більше, чим менше буде незалежних поєднань відхилень, тобто чим більше буде спряженість між ознаками, що варіюють.

При обробці нечисленної вибірки можна скористатися формулою (52):

(52)

Можна скористатися способом «довільного початку» (непрямий спосіб):

(53)

де а_х і а_у – відхилення значень X і Y від свого довільного початку в одиницях інтервалу; f – частота відповідних груп.

Коефіцієнт кореляції може набувати значень від +1 до –1, залежно від тісноти зв'язку. При повній прямій кореляції r=+1, при повній зворотній r=–1. Коли кореляція відсутня, коефіцієнт близький до 0. Зазвичай вважають, що величина r=0,20–0,30 свідчить про наявність слабкої, r=0,50–0,60 – середньої, а r=0,80–0,90 – сильної (тісної) кореляції між ознаками.

3. Обчислення квадратичної помилки коефіцієнта кореляції. За умов, якщо вибірка проведена з нормальної сукупності, помилку коефіцієнта кореляції обчислюють за формулою (54):

(54)

4. Оцінка істотності коефіцієнта кореляції. Коефіцієнт кореляції вважають за істотний, якщо вірогідність появи такої кореляції в свідомо некорелятивній сукупності буде дуже мала. Таким чином, завдання зводиться до оцінки значущості відхилень r від нуля. При великому числі спостережень (n≥30) коефіцієнт кореляції можна вважати за істотний, якщо він перевищує свою помилку в 3 і більше разів, тобто . У нечисленних вибірках істотність коефіцієнта кореляції оцінюється за допомогою критерію t:

(55)

де n – число парних спостережень.

Зіставлення фактичного і табличного t при числі ступенів свободи k=n–1 дає можливим оцінити істотність r при вибраному рівні значущості.

5. Спосіб обчислення коефіцієнта кореляції за допомогою довільного початку. Отримані дані групують у кореляційну таблицю. За довільний початок відліку беруть значення Х і Y, що знаходяться в середині ряду. Наприклад, А_х=10, А_y=22. Рядок і графу відкреслюють жирними або кольоровими лініями. Виходить 4 квадранта. Потім обчислюють відхилення значень інтервальних груп від своїх А, записують їх в рядок а_х і а_у. Обчислюють fa_x, fa_x^2, fa_y^, fa_y².

Після цього обчислюють здобутки a_xa_y для кожної клітки кореляційної таблиці. Наприклад, для першої клітки верхнього рядка a_xa_y=(–3)(–2)=6 і так далі. Ці здобутки записують в тих же клітках кольоровим олівцем або беруть у дужки. Потім підраховують суму всіх fa_xa_y, враховуючи знаки. Таблицю краще розділити на 4 квадранти. a_xa_y кожного квадранта таблиці мають певні знаки: плюс – в лівому верхньому (I) і правому нижньому (III), мінус – в правому верхньому (II) і лівому нижньому куту (IV).

I квадранта = 1·6+2·3+1·4+2·2+1·1=21

II квадранта = 1·(-2)+4·(-1)+2·(-2)= –10

III квадранта = 0

IV квадранта = 2·1+6·2+2·3+..+2·12=73 Разом = 84

Отже, 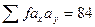; ; ; ; ; ; n=50

.

Далі проводиться оцінка істотності коефіцієнта кореляції.

6. Обчислення кореляційного відношення. У тих випадках, коли попередній аналіз показує, що залежність між двома ознаками має криволінійних характер, коефіцієнт кореляції не дає повного уявлення про ступінь зв'язку між ознаками. В цьому випадку обчислюють показник криволінійної залежності, так зване кореляційне відношення η (ета), що є відношенням двох дисперсій: дисперсії групових середніх і загальній дисперсії. Тобто кореляційне відношення відповідає на питання: яку частину загальної дисперсії результативної ознаки складає дисперсія приватних середніх цієї ознаки. Кореляційне відношення обчислюється за формулою (56):

(56)

де – середнє відношення групових середніх; – середнє квадратичне відхилення Y.

Кореляційне відношення завжди позитивно і набуває значень від 0 до 1. У разі прямолінійного зв'язку коефіцієнт кореляції (його абсолютна величина) і кореляційне відношення рівні. Якщо зв'язок криволінійний, то η>r.

Приклад. У табл. 29 наведені дані про залежність між вмістом жиру і йодним числом у 296 зразків сої. r=–0,100, отже зв'язок між цими ознаками відсутній. В той же час характер змін йодного числа вказує на наявність криволінійної залежності: із збільшенням вмісту жиру йодне число спочатку зменшується з 137 до 126, а потім знов збільшується до 131.

 

Таблиця 29 – Залежність між вмістом жиру і йодним числом у насінні сої

% жиру Х	Йодне число (групова середня)	fy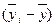
			9,1	82,81	165,62
			7,1	50,41	504,10
			3,1	9,61	182,59
			–1,9	3,61	245,48
			–1,9	3,61	274,36
			1,1	1,21	79,86
			1,1	1,21	53,24
			2,1	4,41	30,87
			3,1	9,61	38,44
Cума					1574,56

 

Для обчислення кореляційного відношення:

1) знаходять середнє вибірки: одиниці;

2) обчислюють відхилення групових середніх від загальної середньої, тобто ;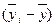

3) квадрати відхилень помножають на частоту f_y;

4) обчислюють середнє квадратичне відхилення групових середніх

;

5) обчислюють звичайним способом (тут не приводиться) σ_y=4,78 одиниці;

6) знаходять кореляційне відношення

Квадратична помилка кореляційного відношення може бути обчислена за наближеною формулою (57):

(57)

У даному прикладі 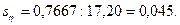З достатньою достовірністю можна вважати кореляційне відношення істотним, коли воно перевершує свою помилку в 3 і більше разів, тобто коли

7. Обчислення критерію криволінійності. При кореляційному аналізі характер зв'язку між ознаками часто вдається визначити за зміною групових середніх. Більш менш правильна, систематична зміна їх від групи до групи (тобто збільшення або зменшення) вказує на наявність лінійної залежності. У таких випадках необхідність в обчисленні їх відпадає.

З іншого боку, якщо характер зміни групових середніх вказує на криволінійну залежність, тоді для характеристики тісноти зв'язку обчислюють кореляційне відношення. Проте в деяких випадках за зміною групових середніх важко судити за характером зв'язку і доводиться обчислювати обидва показники – коефіцієнт кореляції і кореляційне відношення.

Деяке уявлення про характер зв'язку дає різницю η–r; чим вона більша, тим, взагалі кажучи, «більш криволінійна» залежність між ознаками. Але оскільки ці обидва коефіцієнти, як і будь-яка інша статистична характеристика, схильні до випадкових коливань, які можуть бути одно- і різнозначними, необхідно у кожному окремому випадку об'єктивно оцінити, наскільки η відрізняється від r, інакше кажучи, визначити можливі межі випадкових коливанні різниці η–r. Таку перевірку проводять за допомогою критерію криволінійності, користуючись відомим прийомом знаходження відношення

(58)

Чисельником цієї формули є різниця квадратів, а знаменником – помилка цієї різниці, що обчислюється за формулою:

(59)

Розраховану за формулою (58) величину t порівнюють з табличним її значенням при вибраному рівні значущості і числі ступенів свободи, що дорівнює n–2. Різниця η–r вважається за істотну, якщо t_факт дорівнює або більше t_табл. В цьому випадку визнають, що зв'язок між ознаками істотно криволінійний.

Приклад. При перевірці криволінійності зв'язку між вмістом жиру в насінні сої та йодним числом отримані наступні дані: η =0,483; r= 0,100, n=296, η²–r²=0,2233.

Обчислюємо помилку різниці s_η–r за формулою (59):

; .

8. Розрахунок коефіцієнта детермінації. Для тлумачення значень, що є показниками тісноти кореляційного зв'язку, використовують так звані коефіцієнти детермінації, які показують, яка частка варіації однієї ознаки залежить від варіювання іншої ознаки. За наявності лінійного зв'язку коефіцієнт детермінації є квадратом коефіцієнта кореляції , а за нелінійної залежності між ознаками Х і Y – квадрат кореляційного відношення . Так, коефіцієнт детермінації між (Х) надземною і підземною масою (Y) частини рослин складає або 27,4 %. Це означає, що лише 27,4 % варіації ознаки Х визначається варіюванням ознаки Y. Найчастіше застосовують квадрат кореляційного відношення.

Коефіцієнт детермінації дає підставу побудувати наступну зразкову шкалу, що дозволяє робити висновок про тісноту зв'язку між ознаками: при r=0,5–0,6 зв'язок вважається за середній, r<0,5 вказує на слабкий зв'язок і лише при r≥0,7 можна судити про сильний зв'язок, коли приблизно 50 % варіації ознаки Y залежить від варіації ознаки Х.